Force Interactions

At a Distance

Forces are measured in Newtons and can either, push, pull or deform (change the shape of an object). There are two main ways that this can happen, some forces can achieve these changes without any need for there to be any contact between the objects involved. These types of forces are said to be acting at a distance.

These are:

● Gravity

● Magnetic forces

● Electrostatic forces

Gravity

Gravity is a force that acts between any two masses, however, as it is a very weak force its effects are only noticeable if one of the two objects has a very large mass.

Common effects:

Gravitational pull of the sun to hold the planets in orbit.

Gravitational pull of the Earth on the moon and satellites.

Objects falling.

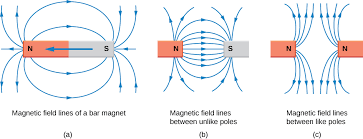
Magnetic Forces

The repulsion and attraction of bar magnets is the most commonly thought of example. The Earth’s magnetic field is used in navigation for the North pole of a compass, and it can pull in charged particles from the sun to create the Northern Lights (Aurora Borealis).

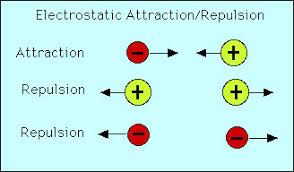
Electrostatic Forces

An electrostatic force of repulsion or attraction exists between any objects that carry an electrical charge. This includes any object that has a charge as a result of static electricity and charged sub-atomic particles, like an electron.

Examples of Electrostatic forces

A static electric charge is applied to particles of ink in a photocopier to produce the print. The paint and the body of a car are given opposite charges in a car paint shop to help the paint fully coat the car body.

Electrically charged particles make up the structure of atoms, electrons (negative) and protons (positive). The electrostatic forces between these particles holds the electrons in orbit about the proton rich nuclei, it also forms the attraction between ions in an ionic bond.

All forces that act at a distance get weaker as the distance between the objects increases.

Contact Interactions

The vast majority of examples of forces that have an affect on the motion or shape of objects are known as _contact interaction forces. _This means that the objects affected by the forces must be in physical contact (be touching) for the forces to have any affect.

This category includes any conventional push or pull and forces like air resistance, grip and friction. In all cases the objects are touching or moving past each other, such as the grip of a bike tyre on the road surface, or the friction created when the brakes are applied on a bike to slow the bike down.

In flight the lift from the wings and in swimming the upthrust of buoyancy are also examples of contact interaction forces.

A contact interaction force acts at the point(s) of contact on the object(s).

Interaction Pairs

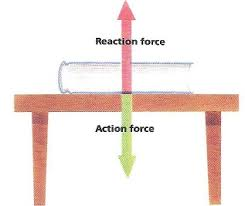
Sir Isaac Newton produced three laws that explain the motion of objects. In his third law he stated that all actions have a reaction, that is equal but opposite. This means that all forces act in pairs and are equal but opposite to each other. These are known as interaction pairs.

When you sit on a chair, you are held on the chair by the pull of gravity. If this was the only force acting on you, you would be falling toward the floor. The fact that you are stationary and sitting on the seat means that there must be a force pushing back up on you to stop you from falling.In this case this is the resistance of the chair and the seat. Its ‘strength’ balances out the gravity so that you do not fall.

When a plane is in flight, gravity is pulling it down towards the ground, but this is balanced by the lift generated by the movement of the wings through the air.

When you push on an object to move it, the object pushes back on you at the point where your hands touch the object. If it didn’t you would bend the object or be able to push your hand through the object!

The action force is the pull of gravity, and the reaction which is equal and opposite to the gravity is caused by the tensile strength of the material of the table.

Vectors and Scalars

Vector and scalars are ways of saying what information must be known to fully describe a quantity in science or maths.

A scalar quantity is fully described by its magnitude (size) only. That is how big or small the value is. Scalars always have a positive value.

Examples:

● Time

● Length

● Mass

● Density

● Molarity

● Area

● Speed

● Electrical charge

● Luminosity

● Energy

Vectors __require one other piece of information to fully describe them, so as well as __magnitude (size) a vector has to have __direction. __Vectors can have both positive and negative values to represent direction.

Examples:

● Forces

● Velocity

● Acceleration

● Momentum

● Moment of a force

Scalar - magnitude (size) only. (e.g. Speed = 10 m/s)

Vectors - magnitude (size) and direction. (e.g. Velocity = 10 m/s North)

Vector Diagrams

Given that a vector, such as a force, must have both magnitude and a direction, they can be represented as a diagram, using arrows.

The length of the arrow is draw to scale to represent the magnitude of the vector.

The arrowhead shows the direction of the vector.

These two arrows are, therefore, vectors of the same magnitude but opposite in directions.

These can be used to combine vectors to work out their overall action.

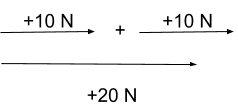
Example: Force addition.

Both forces are acting in the same direction and can simply be added together.

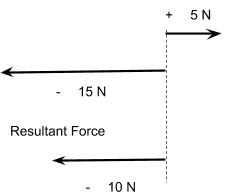
Adding can also be used with forces of opposite signs and directions.

+5 N + -15N = -10 N

When forces are added together, the combined effect is known as the resultant force or the net force.

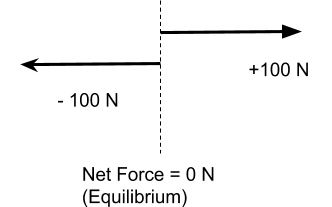
In some situations two forces can be equal in magnitude but opposite in directions, like an equally matched tug-of-war. In these situations the forces cancel each other out so that the net force is zero newtons.

Addition of Forces at an Angle

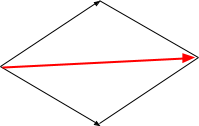
In reality many forces meet at angles to each other, in these situation a scale diagram can resolve the two forces.

1. Draw out the two known forces to scale with the correct angle between the forces where they meet.

1. Complete the rhombus and add an arrow across the diagonal. This arrow represents the magnitude and direction of the resultant force.

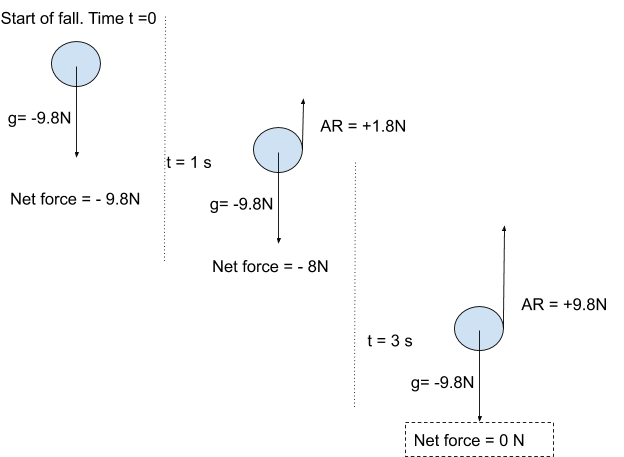
Example of Resultant Forces: Falling Objects and Terminal Velocity.

A 1 kg mass is pulled towards the Earth with a force of 9.8 N/kg. When it is first let go gravity is the only initial force. As it gains velocity the air resistance begins to apply a force in the opposite direction. Eventually the air resistance equals the pull of gravity and the two forces cancel each other out. At this point the falling mass stops accelerating and falls the rest of the way at the same velocity.

g = gravity AR = Air Resistance

Free Body Force Diagrams

For virtually all objects with forces acting upon them, there are normally more than two forces acting. These situations can be drawn as force diagrams called Free Body Force Diagrams.

They differ from the simpler versions of the vector diagrams by showing several different force pairs in a single diagram.

Example: Pushing a box.

The green arrows are; the force of gravity (downwards) and the resistance of the surface (upwards). These are equal and opposite, so cancel each other out.

The red arrows represent the push from the person and the friction between the box and the surface. The push is larger than the friction so the box is accelerating to the right.

Example 2: Plane in Flight

The combination of the four forces acting on the plane, allow the pilot to control the motion of the plane. When all four are in balance the plane will be in straight and level flight at a constant velocity.

Increasing lift will allow the plane to climb.

Rotation

If a force is applied to one end of an object that is fixed in placed at one point the object will rotate or turn about the fixed point. Everyone is familiar with this type of motion from the simple act of opening or closing a door, or playing on a seesaw in the park.

The fixed point about which the object turns is known as the pivot or fulcrum.

The downward force of the weight of the person on one end will make the seesaw move downwards, but because it is constrained in the middle at the pivot, the plank rotates about this point.

In all cases of rotation, which is a form of circular motion, there must be a force directed towards the centre of the turn. This force is known as the centripetal force. In the case of the seesaw this force acts along the plank and is a form of centripetal force known as a tension centripetal force.

The Earth orbiting the sun or the moon orbiting the Earth are both examples of rotational motion. In these two examples the centripetal force is gravity.

Give two examples of forces in action. One of which is caused by a force acting at a distance and one in which there is a contact force interaction.

Your answer should include: gravity pulls / electrostatic attraction / effects of magnets / physical contact
Explanation: Force at a distance: Gravity pulls on an object to make it fall. Gravity holding any object in an orbit about a celestial body, like the moon around the Earth. Electrostatic attraction between sub-atomic particles in an atom, or the repulsion of the protons in the nuclei of atoms. Or the effects of magnets attracting or repelling each other. Contact Forces: Any example where there is physical contact that changes the motion or shape of the objects.

State the difference between a vector and a scalar, giving an example of each.

Your answer should include: magnitude / size / directions / velocity / acceleration / forces / momentum / only have magnitude / speed / mass / time / length / density
Explanation: Vectors have both magnitude (size) and directions, examples would include: velocity, acceleration, forces, momentum. Scalars only have magnitude, examples would include: speed, mass, time, length, density.

If a force of 30,000 N was acting upwards on a plane and the pull of gravity was acting with a magnitude of 29,400. What is resultant force on the plane?

Your answer should include: 600 / 600N / upwards
Explanation: +30,000 + - 29,400 = + 600N or 600 N upwards.