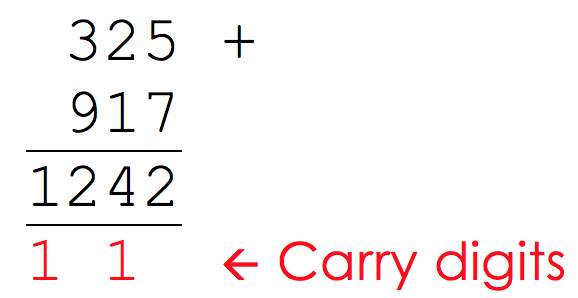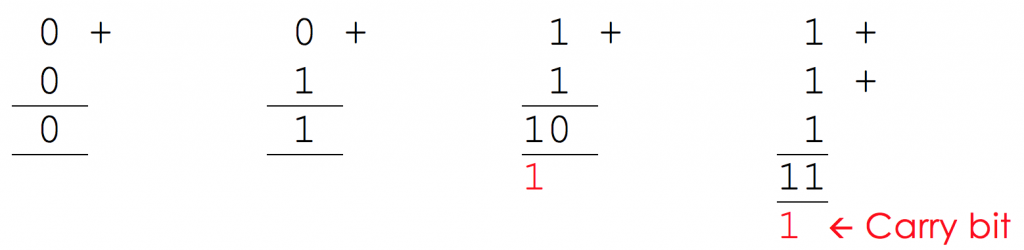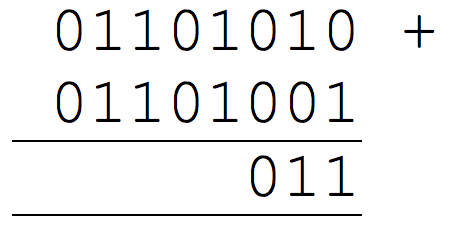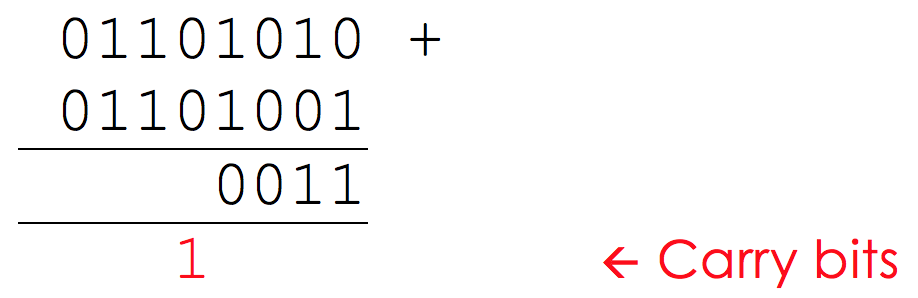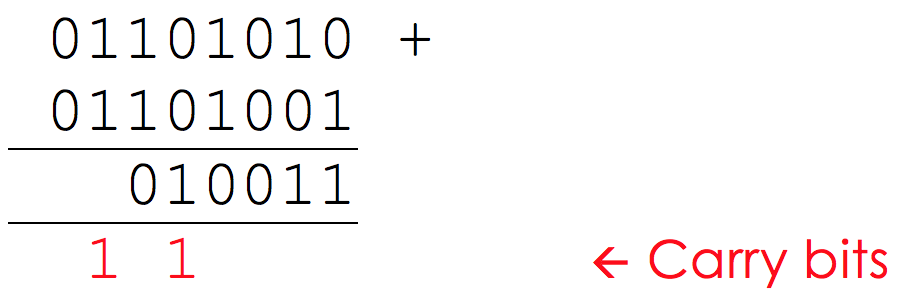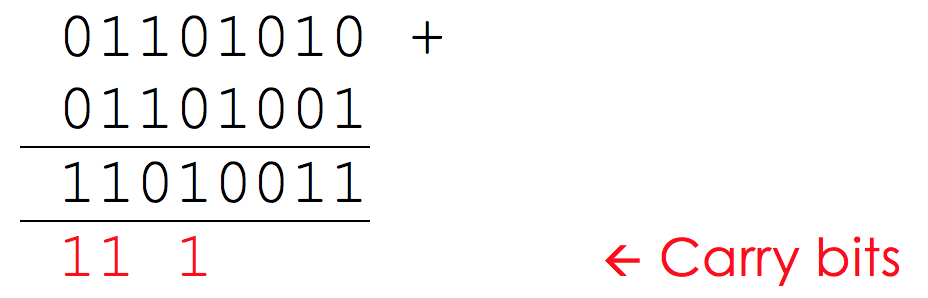Binary Arithmetic

Binary Addition

When adding binary numbers together, it is very similar to using the column method in decimal:

Here, 5+7 is 12, but we can’t write 12 using just the units column so we ‘carry’ the 1 into the tens column and add it to the 2 and 1 already there. We also do the same with the 3 and the 9.

Binary addition is (in some ways) even easier, as there are only a few cases we need to consider:

Under the most recent AQA specification, “students will need to be able to add together up to three binary numbers using a maximum of 8 bits per number. Students will only be expected to add together a maximum of three 1s in a single column. Answers will be a maximum of 8 bits in length and will not involve carrying beyond the eight bits.” Indeed, if you answer exceeds 8-bits (1 byte) then this is referred to as an overflow error.

Example Binary Addition (2 Numbers)

Question

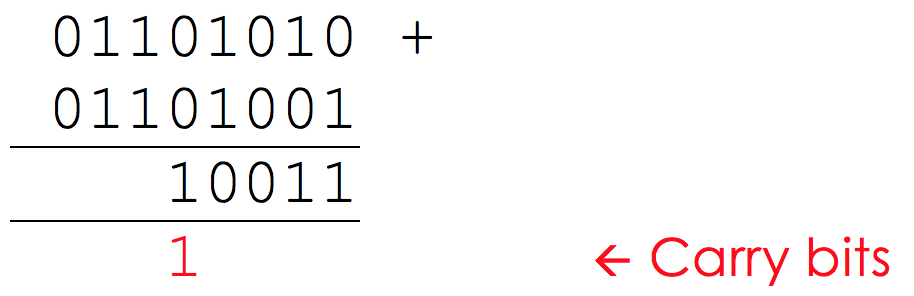
Add together the binary numbers 0110 1010 and 0010 1001.

Solution

To do this addition, always work from the units column on the right. Here, the first there columns are straightforward:

However, the next column is a little trickier. Here we have 1 + 1 = 10, so we need to remember to ‘carry’ the 1:

Now, when we add up the next column, we need to make sure that we include the carried bit in our calculation.

Working along, we see again have another bit to carry as we have 1 + 1 = 10.

Now, in this column, we have 1 + 1, but we also have our ‘carry’ bit to give us 1 + 1 + 1 = 11, so we still need to carry the 1, but we need to remember to also put a 1 in the column we are working in. Finally, we add our last column and get the answer:

We can double check this to make sure everything is working ok…

1. 0110 1010 in binary = 64 + 32 + 8 + 2 = 106 in decimal.
2. 0110 1001 in binary = 64 + 32 + 8 + 1 = 105 in decimal.
3. 106 + 105 = 211 in decimal = 1101 0011 in binary.

Example Binary Addition (3 Numbers)

Question:

Add together the binary numbers 0010 1010, 0100 0110 and 0011 1011.

Solution

The solution works in the exact same way as with 2 numbers, but you are likely to find yourself ‘carrying’ a lot more often!

Again, let’s check the answer:

1. 0010 1010 in binary = 32 + 8 + 2 = 42 in decimal
2. 0100 0110 __in binary = 64 + 4 + 2 = __70 in decimal
3. 0011 1011 in binary = 32 + 16 + 8 + 2 + 1 = 59 in decimal
4. 42 + 70 + 59 = 171 __in decimal = __1010 1011 in binary

What is the answer to these binary additions - answer using 4 or 8 bits as appropriate?

0110

1010

11111111

11010011

11111010

11001110

Two bytes store the following values 1100 0011 and 1000 0010. What is the problem if you try and store the sum of these in a single byte?

overflow error

What is the maximum that could be added to 1001 1011 with the result able to be stored in 1 byte?

01100100

Binary Shift

A binary shift is when the digits of a binary number are moved either to the left or the right for multiplicative or division purposes. These are usually faster than normal multiplication and division

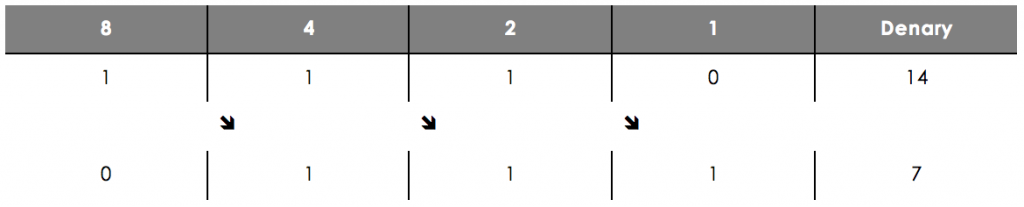
A left-shift represents multiplication by 2. All digits are shifted one position to the left and a 0 is added to fill in the gap at the end.

In a left-shift, if a 1 digit falls off the end, this is an overflow error__. __Here we try and multiply 9 by 2 using just a nibble, but you can see that this results in an answer of 2 – which is incorrect.

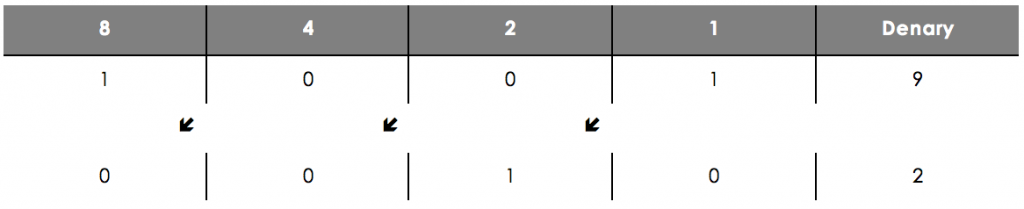
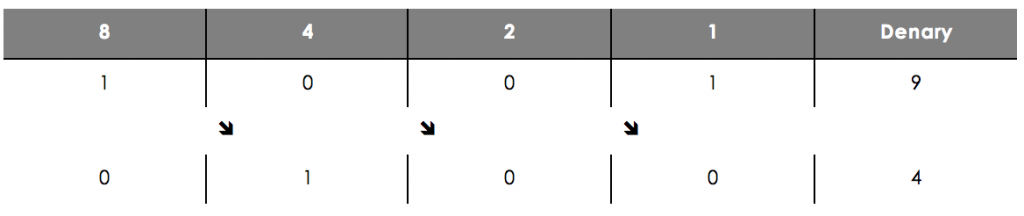
A right-shift represents division by 2. All digits are moved 1 position to the right and a 0 is added to fill the gap at the start.

In a right-shift, if a 1 digit falls off the end, this is an underflow error. Here we try and divide 9 by 2 using just a nibble, but you can see that this results in an answer of 4 – which is incorrect.

We can use multiple shifts to represent multiplication and division by any power of 2. For example, doing 3 left-shifts in a row, would represent multiplying by 2 x 2 x 2 = 8.

Example Question (Division)

Question

Using a shift, divide the number 11001000 by 8.

Solution

Since this is a division, we are going to need to do a right-shift. Since doing 1 shift will divide by 2, we need to carry out three shifts to divide by 8.

First, we do 1 shift, making sure that we add the zero to the beginning:

11001000 goes to 01100100

Now we do another shift to divide again, which will give us our original number divided by 4:

01100100 goes to 00110010

Finally, we do our third shift to divide by 2 again, which will give us our original number divided by 8:

00110010 goes to 00011001

Therefore, 11001000 divided by 8 is 00011001.

Again, let us do a check that it has worked out ok:

1. 11001000 in binary = __200 __in decimal
2. 200 / 8 = 25 in decimal = 11001 in binary.

Example Question (Multiplication)

Question

Using a shift, multiply the number 101001 by 4.

Solution

Since this is a multiplication, we are going to need to do a left-shift. Since doing 1 shift will multiply by 2, we need to carry out two shifts to multiply by 4.

First, we do 1 shift, making sure that we add the zero to the end:

101001 goes to 1010010

Now we do another shift on our new number to multiply by 4:

1010010 goes to 10100100

Therefore, 101001 multiplied by 4 is 10100100.

Let’s just check that everything is working ok…

1. 101001 in binary = 32 + 8 + 1 = 41 in decimal
2. 41 x 4 = 164 in decimal = 10100100 in binary

01001011 multiplied by 2.

10010110

10010010 divided by 2.

01001001

00010011 multiplied by 8.

10011000

10001000 divided by 4.

00100010

What is the name of the error that will occur if trying to do this calculation?10100110 divided by 4

underflow

What is the name of the error that will occur if trying to do this calculation?10111101 multiplied by 2

overflow