Fundamentals of Algorithms

Computational Thinking

Computational thinking is the thought processes involved in formulating a problem and expressing its solution(s) in such a way that a computer—human or machine—can effectively carry out.

Computational thinking is involved in the creation of computer programs, but also covers a much broader area. You will be required to sit a paper about computational thinking, and be expected to solve problems, and create algorithms in the exam.

There are several steps when solving a problem:

  1. Decomposition – Breaking the problem down into smaller sub-problems, so that each sub-problem accomplishes an identifiable task, which might itself be further subdivided.
  2. Pattern Recognition – Finding repeating patterns that could be solved quickly
  3. Abstraction – Removing unnecessary detail from a problem
  4. AlgorithmCreation– Creating a step by step set of instructions to solve the problem.

You will be expected to do all 4 steps regularly.

Algorithms

An algorithm is an unambiguous, step-by-step solution to solve a problem in a finite number of steps. All computer programs are examples of algorithms, but not all algorithms are computer programs. In fact, an everyday example of an algorithm is a recipe.

In general, there are three parts to an algorithm:

  1. Input – the values that are put into the algorithm
  2. Process – what happens in the algorithms
  3. Output – the value (or print out) that the algorithm produces

In the example of a recipe for a cake, what part of the algorithm (input/process/output) are the following?

The finished cake:
output
Mixing:
process
Cooking:
process
The ingredients:
input

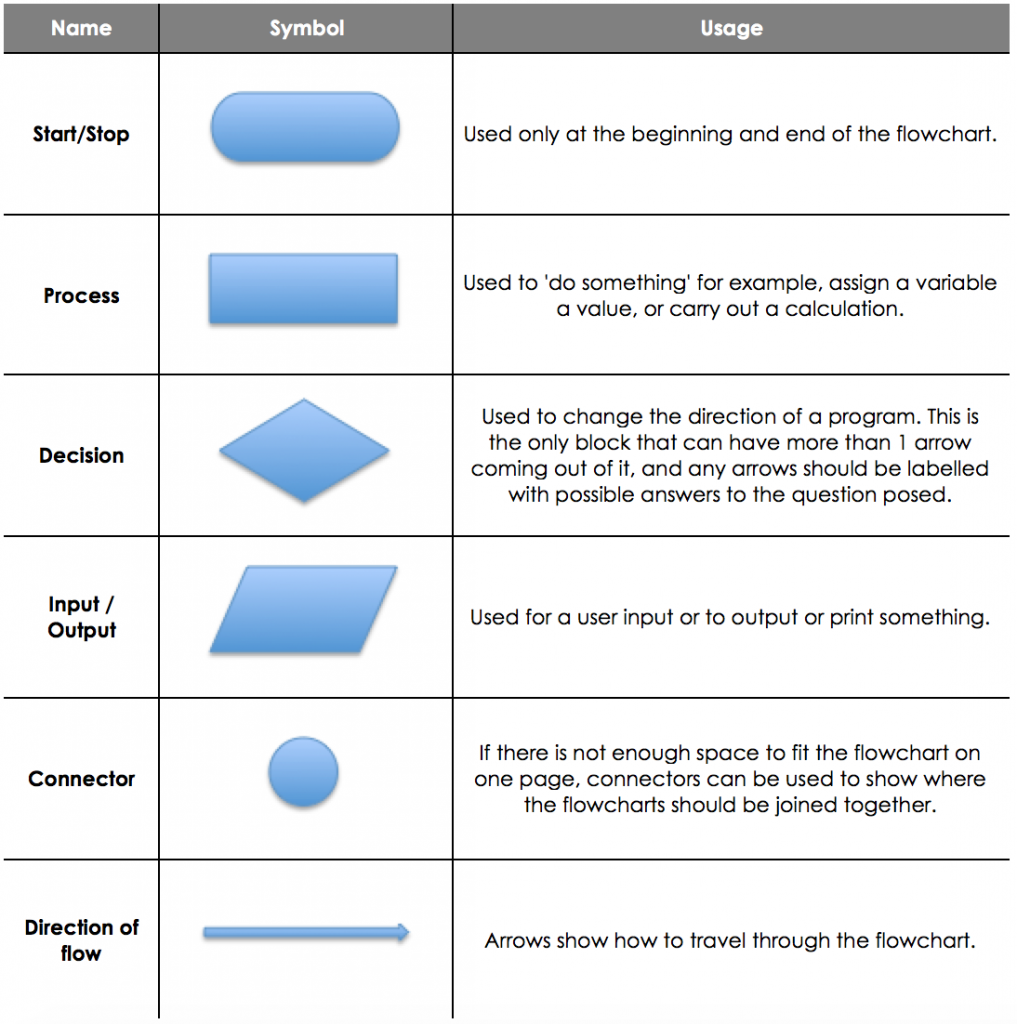
Flowcharts

Flowcharts are a graphical way of displaying an algorithm. There are a number of different boxes to use with flowcharts and each determines what happens at that stage. The important thing to remember about flowcharts is to make sure that you do not miss out any stages, or combine too many together.

Fundamentals of Algorithms, figure 1

Comparing Flowcharts to Pseudocode

In general, pseudocode is much easier to create accurate and detailed algorithms. In flowcharts it is too easy to miss out a step, or combine the hard bits together into one block. However, flowcharts are a much easier way to see the flow of a program and how it runs from start to finish.

You are able to use both in your exam, although it is recommended that you use pseudocode, as you are less likely to drop silly marks. If you use flowcharts, make sure that you have one block for every line of code that you would use if you were programming it, and ensure you label all arrows out of decision blocks correctly.

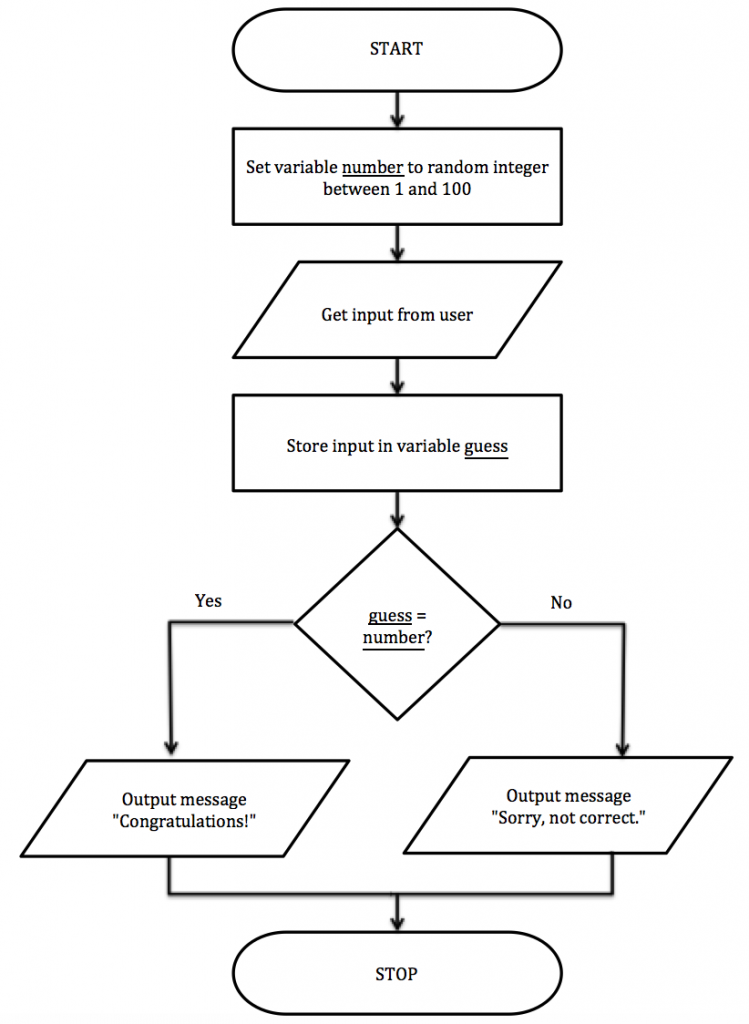
Pseudocode Example

number ← RANDOM_INT(1, 100)

guess ← USERINPUT

IF guess = number THEN

OUTPUT “Congratulations!”

ELSE

OUTPUT “Sorry, not correct.”

ENDIF

Flowchart Example

Fundamentals of Algorithms, figure 2

Pseudo-code

Pseudo-code means ‘fake code’. It is text that is written programmatically but designed to be read by humans and not a machine. There is no standard convention on what pseudocode should look like; the advantage of pseudocode is that anyone can read it regardless of which languages they are able to code in.

In the exams, AQA will use a standard set of pseudocode. This can be searched online using ‘AQA pseudocode’ and is worth familiarising yourself with the notation.

Useful examples from it include:

Variable AssignmentIDENTIFIER ← valuea ← 3
User Inputvariable ← USERINPUTa ← USERINPUT
Output (Print)OUTPUT StringExpOUTPUT a
Random IntegerRANDOM_INT(IntExp, IntExp)RANDOM_INT(3, 5)
Comments# comment# will randomly generate 3, 4 or 5

All other commands will be covered in the programming techniques lesson.

Trace Tables

When trying to determine the purpose of an algorithm, it is useful to go through it line by line, and ‘run it’ manually. This is called doing a dry run, and will help you to work out what exactly is going on. It is also a useful technique when debugging code.

Trace Tables__ are a way for us to track the value of a variable through a program. They are very useful for helping to identify __logic errors__ __– these are errors where the program doesn’t do what we expect.

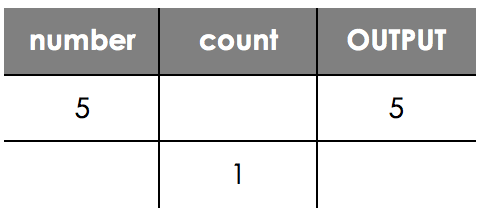
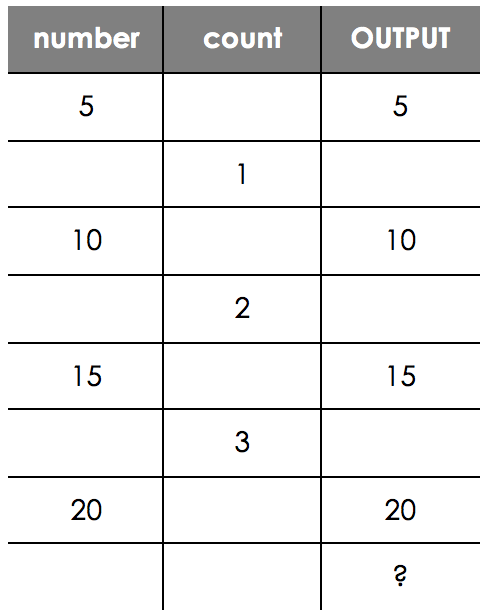
Here is an example of an algorithm:

1 number ← 5

2 OUTPUT number

3 FOR count ← 1 TO 3

4 number ← number + 5

5 OUTPUT number

6 ENDFOR

7 OUTPUT “?”

There are 2 different variables we need to keep track of here, as well as what the program outputs. So we fill in a table of the values as they change through the program.

Let’s see what happens. In the first line of code, number is changed to 5 so we write this in our table. Then on the second line we see an OUTPUT, so we can also add that.

Fundamentals of Algorithms, figure 1

You can see here we have missed out the value of count, as this has not changed. However, on the next line (line 3), count changes.

Fundamentals of Algorithms, figure 2

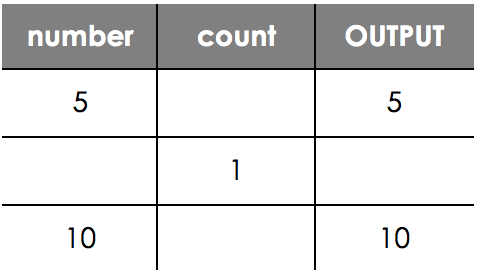
On line 4 now number is changed again, and we get a further OUTPUT on line 5, so we can add them both in.

Fundamentals of Algorithms, figure 3

Now we are looping, count will increase again, and we keep working through our code like this until we reach our final trace table.

Fundamentals of Algorithms, figure 4

Exam Question Using Trace Tables

Here is a typical exam question you may be asked about algorithms. If you are not sure on the syntax (words) used, or how to read the program, look at the programming techniques lesson.

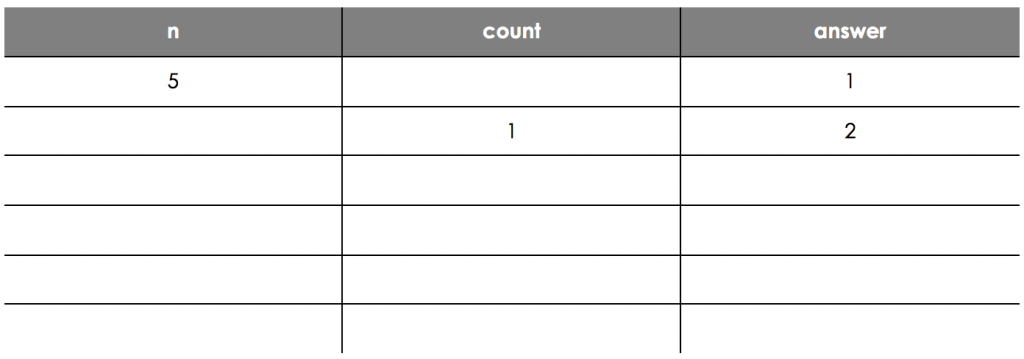
A sequence of numbers begins 2, 4, 7,… Here is an algorithm in pseudo-code for a function that returns the nth number of the sequence. For example, SequenceItem(3) returns the 3rd number in the sequence.

1 SUBROUTINE SequenceItem(n)

2 answer ← 1

3 FOR count ← 1 TO n

4 answer ← answer + count

5 ENDFOR

6 RETURN answer

7 ENDSUBROUTINE

Using the algorithm complete the trace table to calculate the value of SequenceItem(5).

Fundamentals of Algorithms, figure 5

What is your expected trace table values reading down the 'answer' column (don't include the 1 and 2 already there). Make sure you separate each answer with a space.
Your answer should include: 4 / 7 / 11 / 16

Efficiency of Algorithms

There are lots of different ways in which we could solve problems. For example you could cook a cake at 180o or 200o and the result will still be a cake. However, each method will have different benefits and one is more efficient than the other – the cake cooked at 200o will cook faster than the one at 180o.

This is the same thing for algorithms. We can compare how efficient algorithms are by calculating how much time they take to complete a task and we can estimate that by working out how many calculations are required for the algorithm to be completed.

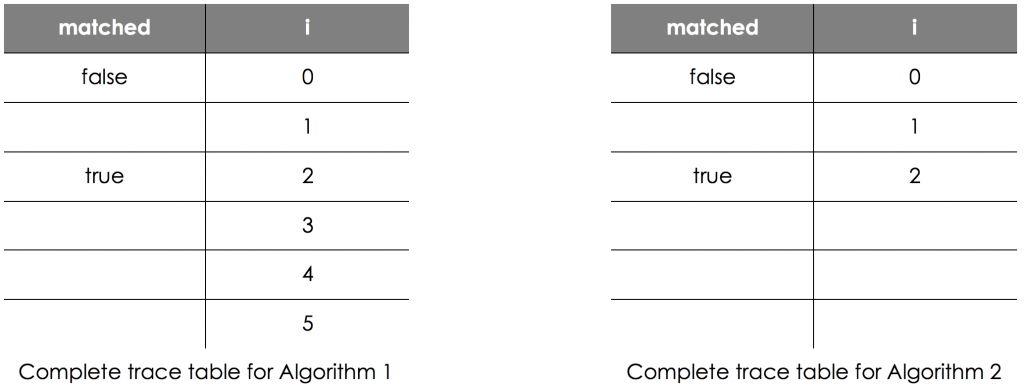
Here is a typical exam question relating to efficiency of algorithms, along with the accepted marks from the markscheme. Two algorithms Algorithm 1 and Algorithm 2 are shown below. Both algorithms have the same purpose.

Fundamentals of Algorithms, figure 1

The completed trace tables for the two algorithms are shown below when the array arr is [‘kleene’, ‘diffie’, ‘naur’, ‘karp’, ‘hopper’].

Fundamentals of Algorithms, figure 2

Both algorithms use a variable called i for the same purpose. State the purpose of the variable i.

Algorithm 1 and Algorithm 2 both have the same purpose. State this purpose.

Give one reason why Algorithm 2 could be considered to be a better algorithm.