Hooke's Law

Hooke’s Law

The extension of an object, whilst elastically deforming, is directly proportional __to the force applied - provided that the __limit of proportionality is not exceeded.

The limit of proportionality is the point where the object no longer deforms elastically, and starts to deform inelastically.

This law is also known as Hooke’s Law.

It comes with an equation which you need to be able to recall and apply:

Hooke's Law, figure 1

The extension can still show if an object is compressed by having a minus sign. This means that the extension is going in the opposite direction, therefore a compression.

Let’s do an example together: calculate the force required to stretch a spring 5cm. The spring constant of the spring is 120N/m.

The first step is to convert the 5cm into metres. 5cm = 0.05m.

Now we can substitute and calculate: F = k x e

F = 120 x 0.05 = 6N

Don’t forget units.

Energy

Who remembers this from the Energy topic?

Hooke's Law, figure 1

Yeah!! Me too!!! Anyway, it is good time to use this again (since it comes up again).

A spring has a spring constant of 25N/m and it has an original length of 2.5cm. If is it extended to __18cm __how much elastic potential energy will be stored in the spring? (4 marks)

The first step is to work out the extension in metres.

0.18 - 0.025 = 0.155m

Then we can calculate this in our equation:

Ee = 0.5 x 25 x x0.1552 = 0.30 J

This second line of calculation contains three marks! One for working, one for the answer and one for units.

A spring has an original length of 2.5cm which extends to 8cm __when a force of __3N has been added to it. Calculate the elastic potential energy which will be stored in this spring once it has been extended.

Step 1: Find the extension

e = 0.08 - 0.02 = 0.055m

Step 2: Calculate the spring constant

F = ke

k = F/e

k = 3 / 0.055 = 54.5N/m

Step 3: Plug this into the elastic energy formula.

Ee = 0.5 x 54.5 x 0.0552 = 0.0824J

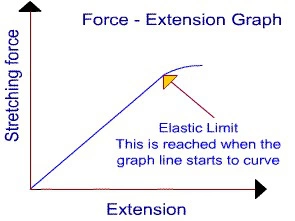
Force and Extension

Wherever a material obeys Hooke’s Law, the relationship between force and extension are directly proportional. However if the material distorts inelastically, force and extension are not proportional.

Hooke's Law, figure 1

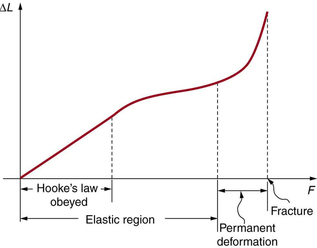
A more detailed graph is shown below, but the above graph is one required for examinations.

Hooke's Law, figure 2

A spring has been extended by 10cm from its original length. Calculate the spring constant given the spring currently stores 0.3J of elastic potential energy?
60N/m
A spring has an original length of 3cm which extends to 9cm when a force of 4.5N has been added to it. Calculate the elastic potential energy which will be stored in this spring once it has been extended.
0.135J