Half Lives

Radioactive decay is a random process. It is impossible to predict exactly when a nucleus will decay or which nucleus in a sample will decay. Despite this random process, all radioactive decays follow the same pattern and all samples have something called a half life:

The time it takes for the number of nuclei of the isotope in a sample to halve.

The time it takes for the count rate (or activity) from a sample containing the isotope to fall to half its initial level.

For example if there is a sample that has a count rate of 100 counts per minute (cpm) and it takes 30 seconds for it to reach a count rate of __50 cpm __then 30s is the half life for the sample.

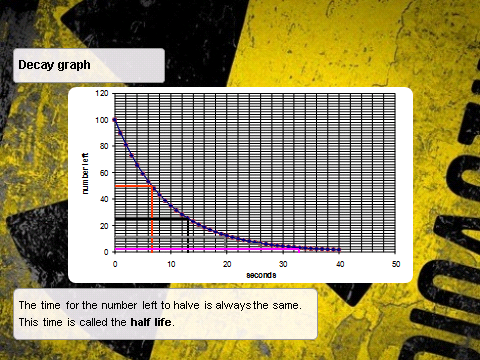
Half Life Graph

Half Life Calculations

Some half life questions will be answered by reading a graph whilst other will be a calculation.

Graphs:

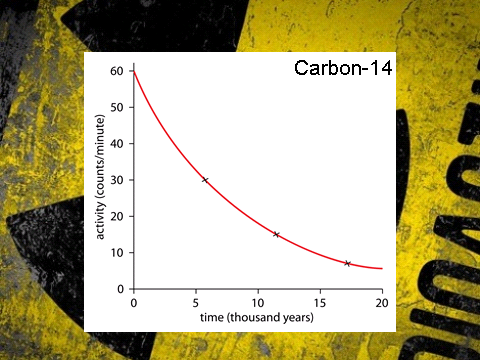
In finding the half life in this case you take any point on the y-axis, normally the intercept, and then you go to the point on the y-axis which is half of the original value. In this case we start with 60 and so half is 30.
We then draw a line from 30 across to the line of best fit, then down and then read off our value. In this case it would be 6000 years. Notice the unit for time. It does not have to be seconds and can go up to millions of years!
The half life for this sample of Carbon-14 is 6000 years.

Calculation: The count rate of a material is 2016 Bq. After 35 days it has fallen to 63 Bq. What is the half life?

Step one: To work this out we need to see how many times we need to half 2016 to get 63.

2016/2 = 1008
1008/2 = 504
504/2 = 252
252/2 = 126
126/2 = 63
```
= Five times
```

Step two: Divide the duration it took to fall to our new value by the number of times we had to half our original value.

35 / 5 = 7 days

Half life = 7 days

Try this: what is the half life of this sample?

Answer: 8 days

The count rate of a material is 200Bq. After 6 years it has fallen to 25Bq. What is the half life?: 2 years