Classification of Stars
Classification by Luminosity
Apparent Magnitude
Apparent magnitude is the perceived brightness of a celestial object from Earth. It is a qualitative scale of brightness which decreases as the brightness increases. A star could be brighter than another star for two possible reasons. It is closer or it is emitting more power at visible wavelengths.
Scale of apparent magnitudes
App. Mag. Celestial object
−26.73 Sun
−12.6 Full Moon
−8.0 Maximum brightness of an Iridium Flare
−4.4 Maximum brightness of Venus
−4.0 Faintest objects observable during the day with naked eye
−2.8 Maximum brightness of Mars
−1.5 Brightest star at visible wavelengths: Sirius
−0.7 Second brightest star: Canopus
0 The zero point by definition: This used to be Vega
3.0 Faintest stars visible in an urban neighbourhood
6.0 Faintest stars observable with naked eye
12.6 Brightest quasar
27 Faintest objects observable in visible light with 8m ground-based telescopes
30 Faintest objects observable in visible light with Hubble Space Telescope
Hipparcos Scale
The Hipparcos scale is the original scale for apparent magnitude, created back in Ancient Greece. His scale goes from 1 (the brightest) to 6 (the dimmest).
Brightness and Apparent Magnitude
The relationship between brightness and apparent magnitude is as follows:
A difference of 1 on the magnitude scale is equal to an intensity ratio of 2.51.
Absolute Magnitude M
__Parsec and Light Year __
The AU (astronomical unit) is the mean distance from the Sun to the Earth and has a value of 1.5 × 1011m.
The light year is the distance travelled by light in a vacuum in one year. It can be easily converted into metres by multiplying the speed of light in a vacuum (3 × 108ms-1) by the number of seconds in a year (365 × 24 × 3600) to get 9.46 × 1015m.
The parsec is the distance from which 1 AU subtends an angle of 1 arc second (1/3600th of a degree), this is most easily defined from a diagram such as this on the right:
1 arc sec is a very small (1/3600) fraction of a degree.
The parsec is an important unit because of the way distances to nearby stars can be determined - trigonometrical parallax. This involves measuring how the apparent position of a star, against the much more distant background stars, changes as the Earth goes around the Sun.
At 10 pc, the angle subtended by the arc second is 10 AU. (1Mpc (mega-parsec) = 106pc)
Absolute Magnitude
The absolute magnitude (M) of a star is the apparent magnitude it would have if placed at a distance of 10 pc from an observer. It is a measure of a star’s inherent brightness. This means that absolute and apparent magnitudes are measured on the same logarithmic scale.
As light intensity reduces in proportion to the inverse square of the distance, the relationship between apparent and absolute magnitude can be related to distance, d, by the equation:
[ m - apparent magnitude; M - absolute magnitude; d - distance (pc)]
Classification by Temperature Black-Body Radiation
Stefan’s and Wein’s Laws
Stefan’s law, also known as Stefan=Boltzmann law relates the power or luminosity and the temperature of a star. It also takes into account the size of the star.
“The total energy per unit time radiated by a black body is proportional to the fourth power of its absolute temperature.
Wien’s displacement law states that the peak wavelength is λmax which is the wavelength at which maximum energy/intensity is radiated. This is inversely proportional to the Kelvin temperature.
Black Body Curves
We are used to the terms ‘red hot’ and ‘white hot’ when applied to sources of heat. We are also aware that hot objects emit radiation at infrared wavelengths.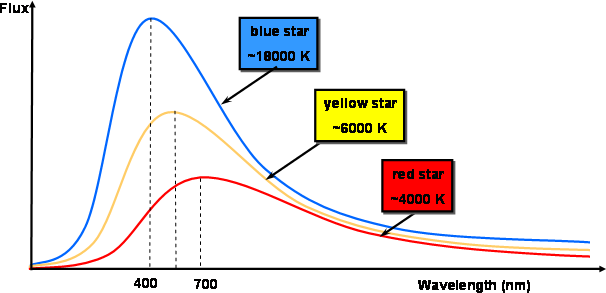
A black body is one that absorbs all the EM radiation that falls on it. Analysis of the intensity of the EM radiation emitted from a black body at different wavelengths produces the following result:
A perfect absorber is a perfect emitter. Therefore if we heat it up it will emit radiation including visible light. This is true (to a first approximation) for stars.
Note the following for black bodies:
• a hot object emits radiation across a wide range of wavelength;
• there is a peak in intensity at a given wavelength;
• the hotter the object the higher the peak;
• the hotter the object the shorter the peak wavelength.
• the area under the graph is the total energy radiated per unit time per unit surface area.
Stefan’s Law Quantitatively
Stefan’s Law:
Sometimes ‘P’ is given as ‘L’ for luminosity.
𝜎 = Stefan’s constant
A = Area
__T __= Temperature (Kelvin)
Or
Where __r __= the star’s radius
Principles of the Use of Stellar Spectral Classes
Stars are split into different classes, called spectral classes. This is done by their temperature, which also relates to their colour.
You need to know this table off by heart:
Temperature
The relationship between temperature and spectra is due to the effect of the energy on the state of the atoms or molecules. At low temperatures, there may not be enough energy to excite atoms, or break molecular bonds, resulting in the TiO and neutral atoms in the M class spectra.
At higher temperatures atoms have too much energy to form molecules, and ionisation can take place (as seen in classes F and G). The abundance of hydrogen and helium in the atmosphere of the hottest stars means that their spectral lines start to dominate. The Hydrogen Balmer series is a useful indicator here.
The electrons start in the n=2 state. To achieve this with a significant proportion of the hydrogen, the atmosphere of the star must be fairly hot. Any hotter than about 10000 K, however, and the hydrogen starts to be ionised.
When the electrons de-excite, the light is emitted in all directions, and the electrons may do it in several steps or miss out n=2 and jump down to n=1. This results in the gap, or reduction in intensity in the direction of the observer.
The name given to the spectrum produced when transitions from n=2 are made is the Hydrogen Balmer Absorption Spectrum
In terms of the Balmer series, the following points can be noted:
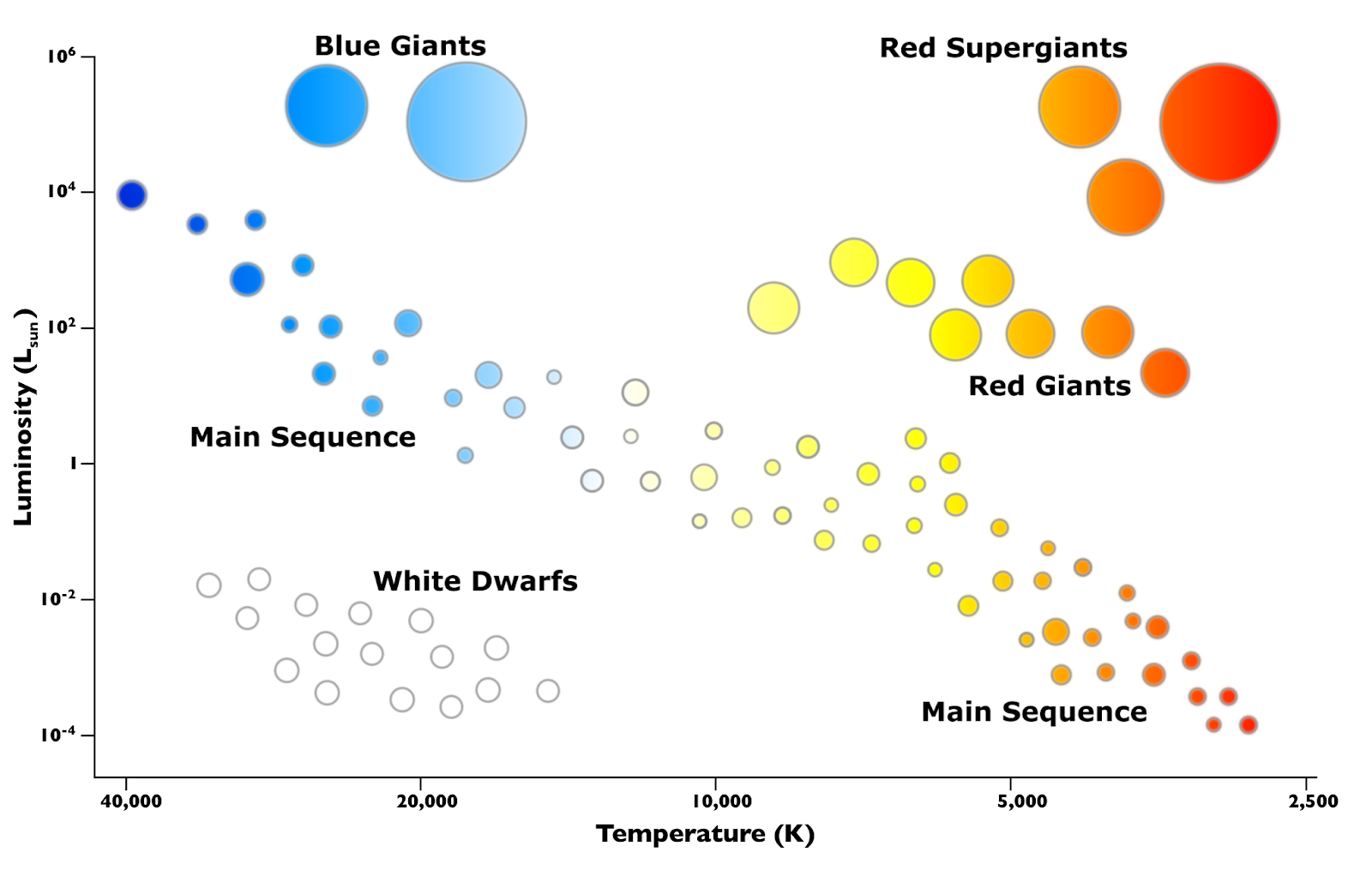
The Hertzsprung-Russell(HR)Diagram
General Shape
The Hertzsprung-Russell Diagram is a graph that shows the luminosity of a star against its temperature. Different stars can be classes into different groups which are shown on the HR-diagram. There is a very high chance that you will be asked to draw and identify/place where different stars go in the diagram. You just need to learn it extremely well.
Or
Stellar Evolution
A star’s life will take it all over the graph when it starts as a planetary nebula and ending as as a white dwarf.
A Star is Born
Gravity is the driving force behind the birth of a new star. It causes particles to come together and collide. This happens increasingly frequently and the temperature begins to rise. Star formation tends to happen where the clouds are dense and have a mass about a hundred times that of the Sun. There needs to be regions of non-uniform density. Stars are usually born in clusters.
As the gas cloud collapses and heats up and is a protostar. At this stage the temperature is still too low for nuclear fusion to happen. If the mass is too low, the failed star ends up as a brown dwarf. As the material gets hotter, molecules are torn apart and atoms are ionised. As the mixture gets hotter still a plasma is formed where atoms are stripped of most, if not all their electrons. Finally an ignition temperature is reached and fusion starts.
Stable Phase of a Star
Nuclear fusion releases a lot of energy. Humans have achieved it but only in the context of an explosion that would make a thunderclap like a whisper. The largest fusion bombs used deuterium (an isotope of hydrogen) to produce Helium. The amount of fused gas used would fill little more than a large party balloon. So why does a star not fly apart?
There are two opposing forces:
• Gravity trying to make the star collapse in on itself;
• The outward force of the explosion (sometimes called the hydrostatic pressure).
In the lifetime of a star, the two forces balance each other out and the star remains the same size.
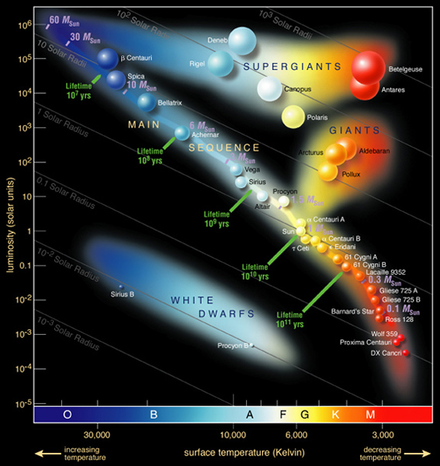
Evolution of a Star
The Sun is a typical star. It would have taken about 1000 years to coalesce into a protostar of about 20 solar diameters, with a luminosity of about 100 times its present value. The evolutionary path taken by more massive stars is shorter, because there is more gravity.
This diagram shows the evolution of stars of different masses. The letter M refers to the solar mass, so 10 M is 10 solar masses. The blue lines are the time spans in years.
So let’s trace how the Sun evolved before it joined the main sequence (thick red line). The luminosity would have been about 100 times what it is now for a period of about 10 000 years. Over the 8 million years the luminosity reduced to its present value. The temperature was relatively low, about 3000 K. Finally over a period of about 10 million years the temperature gradually rose to about 6000 K.
Stars of small mass (less than about 0.8 M) can take 10 000 000 years to reach the main sequence. Stars of mass 0.5 M may not even reach the main sequence at all.
Lifetime of a Star
Most stars spend most of their life on the main sequence of the HR diagram. The life of a star is governed by its luminosity and mass:
• the greater the mass, the longer it will before the hydrogen fuel runs out.
• the greater the luminosity, the sooner it will use up its supply of fuel.
Stars usually start off with 73% hydrogen, 25% helium, and 2% other elements. Our Sun has used up most of its hydrogen and has more helium than hydrogen. It is using about 4 million tonnes of hydrogen every second. The Sun has been burning for about 4500 million years. There is enough hydrogen to last the Sun another 4500 million years.
Stars of 25 solar masses last only a few million years, since they are extremely bright. Stars of less than 1 solar mass burn themselves out very slowly; a star of 0.5 M can last up to 200 000 million years.
Dying Star
The centre of a star is where the fusion takes place. The outer regions are not hot enough and there is still hydrogen in a shell about the core. There is no convective circulation of gases into the core.
As fusion dies down, the expansive pressure reduces and gravity pulls the gases in. They heat up and the pressure on the helium in the core rises. Helium nuclei fuse to form heavier elements. Hydrogen fusion increases in shells outside the core. Therefore there is more helium and the core expands.
Meanwhile while the outer shell where there is hydrogen fusion moves outwards, and the star swells. The star becomes a giant. The core and the hydrogen fusion shell are relatively small, while the majority of the space of a red giant is taken up with a low density envelope.
When the Sun has reached this stage, all the inner planets would have been engulfed and fried to a crisp. Jupiter and Saturn will lose their gas layers to reveal their rocky cores.
In the Sun, elements like carbon and oxygen will be formed in the core. In more massive stars the conditions in the core will be sufficiently extreme further fusion will take place so that, for example, silicon nuclei will fuse to form iron (the most stable nuclide).
Eventually gravity will overcome the expansive force. In small stars, there is convection so that all the hydrogen fuses. However the temperature never gets hot enough for helium fusion to happen. The star collapses under gravity to become a white dwarf. The volume is about the same as that of the Earth. Eventually it cools to a black dwarf, a lump in space.
Supernovae Neutron Stars & Black Holes
The Star’s End
Supernovae are objects which exhibit a rapid and enormous increase in absolute magnitude. Type 1a supernovae are useful because they reach the same peak value of absolute magnitude, making them standard candles, ie the absolute magnitude is known, the apparent magnitude can be measured, so the distance can be determined.
The diagram shows the light curve of a typical type 1a supernova. The peak value of absolute magnitude is -19.3, and occurs after about 20 days from the start of the increase in brightness.
Conventionally time is measured from the peak.
The white dwarf increases in mass as it attracts material from its companion. Eventually the white dwarf reaches a size which allows fusion to start again, (the fusion of carbon which requires very high pressures and temperatures), which causes the star to explode.
This occurs when the star reaches a critical mass, and produces a very consistent light curve. The other advantage of using Type 1a supernovae as standard candles is that they are very bright. This means they can be used to measure the distance to the furthest galaxies.
During the supernova outburst, elements heavier than iron are produced as free neutrons produced in the explosion rapidly combine with heavy nuclei to produce heavier and very rare nuclei like gold, platinum, uranium among others. The superheated gas is blasted into space carrying a lot of the heavy elements This explosion is a supernova. As the expanding gas crashes into the surrounding interstellar gas at thousands of km/s, the shock wave heats up the interstellar gas to very high temperatures and it glows.
Some energy goes into driving the gas envelope outward. The rest of the energy goes into making the supernova as bright as 1011Suns (as bright as an entire galaxy)! Supernovae are very rare—about one every hundred years in any given galaxy—because the stars that produce them are rare. However, there are billions of galaxies in the universe, so simple probability says that there should be a few supernovae happening somewhere in the universe during a year and that is what is seen! Because supernovae are so luminous and the energy is concentrated in a small area, they stand out and can be seen from hundreds of millions of light years away.
If the core has a mass between 1.4 and 3 solar masses, the neutrons will bump up against each other to form a degenerate gas in a neutron star about the size of small city. The neutrons prevent further collapse of the core. Their densities are much larger than even the incredible densities of white dwarfs: 2 × 1014 times the density of water (one sugar cube volume’s worth has a mass = mass of humanity)! Recently, the Hubble Space Telescope was able to image one of these very small objects. Even though it is over 660,000 K, the neutron star is close to the limit of detectors because it is at most 27 kilometres across.
If the core remnant has a mass greater than 3 solar masses, then not even the super-compressed degenerate neutrons can hold the core up against its own gravity. Gravity finally wins and compresses everything to a mathematical point at the centre. The point mass is a black hole. Only the most massive, very rare stars (greater than 10 solar masses) will form a black hole when they die. As the core implodes it briefly makes a neutron star for just long enough to produce the supernova explosion.
The super compact point mass is called a black hole because the escape velocity around the point mass is greater than the speed of light. Since the speed of light is the fastest that any radiation or any other information can travel, the region is totally black.
The distance at which the escape velocity equals the speed of light is called the event horizon because no information of events occurring inside the event horizon can get to the outside. The radius of the event horizon in kilometers = 3 × core mass in solar masses.
Supermassive black holes are found in the centre of galaxies, the larger the galaxy the large the black hole in the middle.
Event Horizon
The event horizon can be found around a black hole and it is the point at which, after crossed, it is impossible to get out.
The radius of the event horizon is called the Schwarzchild Radius. F
kinetic energy = gravitational potential energy
Rearranging gives:
The escape velocity of light can be similarly worked out:
So the Schwarzchild radius is given by:
[Rs - Schwarzchild radius (m); G - universal gravity constant 6.67 x 10-11 N m2 kg-2; M - mass of the star (kg); c - speed of light (m/s)]