Capacitance

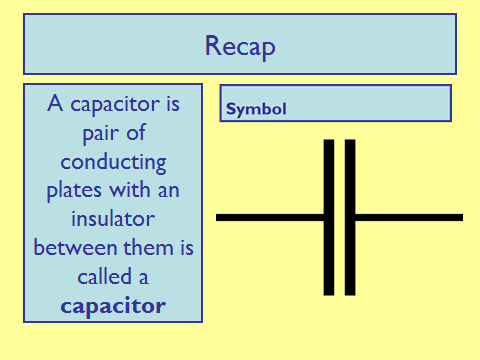
Capacitance

Capacitance, figure 1Capacitance, figure 2

Parallel Plate Capacitor

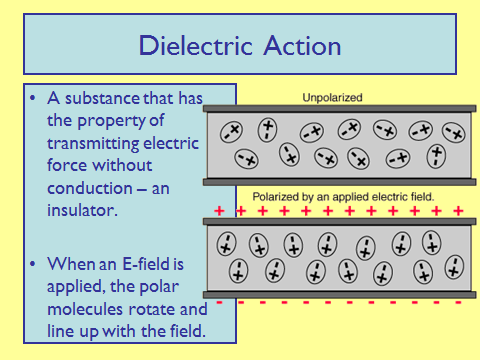
Dielectric Action

Capacitance, figure 1Capacitance, figure 2

Capacitance, figure 3

Energy Stored by a Capacitor

Energy Storage

Capacitance, figure 1

Initially a charged capacitor stores 1600 μJ of energy. When the pd across it decreases by 2.0 V, the energy stored by it becomes 400 μJ. What is the capacitance of this capacitor?
Your answer should include: 200 / 200μJ
Explanation: 200μJ

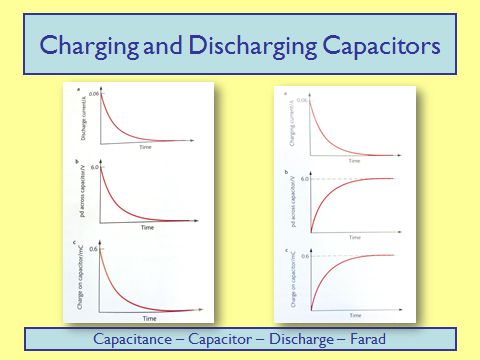
Capacitor Charge and Discharge

Graphical Representation

Capacitance, figure 1

Time Constant

Capacitance, figure 2

Time Taken

The time taken for the capacitor to fall to half its value is:

Capacitance, figure 3

Discharge

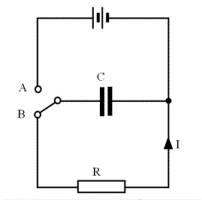
Consider the circuit shown:

Capacitance, figure 4

When the switch is in position A, the capacitor C gains a charge Qo so that the pd across the capacitor Vo equals the battery emf.

When the switch is moved to position B, the discharge process begins. Suppose that at a time t, the charge has fallen to Q, the pd is V and there is a current I flowing as shown. At this moment:

I = V / R (equation 1)

In a short time Dt, a charge equal to DQ flows from one plate to the other so:

I = –DQ / Dt (equation 2)

(with the minus sign showing that the charge on the capacitor has become smaller)

For the capacitor: V = Q / C (equation 3)

Eliminating I and V leads to DQ = – (Q/CR) ´ Dt (equation 4)

Equation 4 is a recipe for describing how any capacitor will discharge based on the simple physics of equations 1 – 3. It can be used in a spreadsheet to calculate how the charge, pd and current change during the capacitor discharge.

Equation 4 can be re-arranged as:

DQ/Q = – (1/CR) ´ Dt

(Showing the constant ratio property characteristic of an exponential change i.e. equal intervals of time give equal fractional changes in charge.)

We can write equation 4 as a differential equation: dQ/dt = – (1/CR) ´ Q

Solving this gives: Q = Qoe-t/CR where Qo = CVo

Current and voltage follow the same pattern. From equations 2 and 3 it follows that

I = Ioe-t/CR where Io = Vo / R

and V = Voe-t/CR

Charge

For charging a capacitor, the relation follows that:

Q = Qo(1-e-t/CR)

A capacitor of capacitance 120 μF is charged and then discharged through a 20 kΩ resistor. What fraction of the original charge remains on the capacitor 4.8s after the discharge begins?
0.14