Gravitational Fields
Newton’s Law
Gravity
Gravity is an attractive force that acts on all matter.
Gravitational Force
Newton’s law of gravitation states that: The force of attraction between two masses is the product of the masses and inversely proportional to the square of the distance between them.
This can also be written as:
__F __= Force (N)
__G __= Universal gravitational constant (this is NOT 9.81 N/kg)
__M __= Mass of one object (kg)
m = Mass of second object (kg)
r = Distance between the two gravitating objects (m)
Gravitational Field Strength
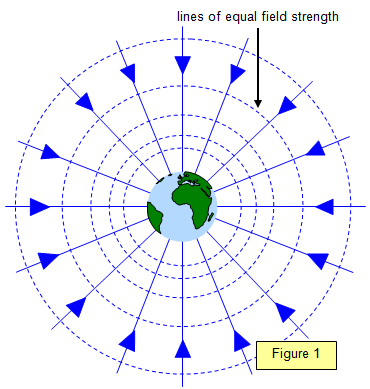
Gravitational Field Lines
A field can be drawn by drawing lines showing where the field acts. In the case of a gravitational field, you have all the lines pointing directly into the centre of mass of the object. Gravitational fields are radial fields, but at a very local level they are uniform. The closer the lines are together, the stronger the field.
In is vital that when asked to draw lines you;
- Use a ruler
- Ensure you have arrows
Define Gravitational Field Strength
Gravitational field strength is the measure of how much force is exerted over a given mass;
g = gravitational field strength (N/kg) [On Earth this is approx 9.81N/kg]
F = Force (N)
m = mass (kg)
Magnitude of Gravitational Field Strength
The magnitude of ‘g’ in a radial field is:
- A satellite is orbiting above the Earth. Calculate that the gravitational field strength of the Earth at the position of the satellite.
- 0.56
Explanation: 0.56 N kg–1
Gravitational Potential
Gravitational Potential
Work Done
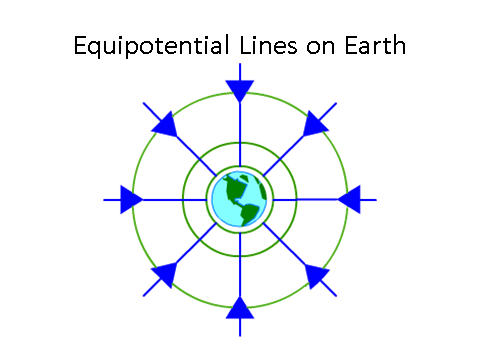
Equipotential Surfaces
The equipotential lines below are in green.
Gravitational PotentialIn a Radial Field
Gravitational potential in a radial field is described as follows:
Gravitational Potential and Gravitational Field Strength
Gravitational potential and gravitational field strength are related as follows:
Notice how the field strength is potential divided by the amount it has moved. Scroll up again to see the difference between gravitational potential and gravitational field strength. Then come back and reread the equation.
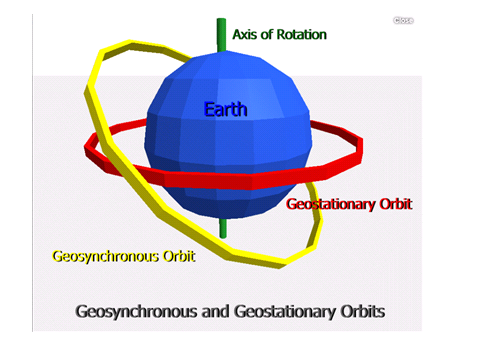
Orbits of Planets and Satellites
Circular Orbit
Orbiting Satellites
Escape Velocity
The minimum speed at the Earth’s surface that will allow an object to leave/escape the gravitational field with no further energy input = Escape velocity.
For normal rockets, they do not start at this speed as they are continuously inputting energy from the engines.
Orbits