Force Energy & Momentum

Scalars & Vectors

A scalar quantity is one that only has a magnitude.

Examples include:

A vector quantity is one that has magnitude and a direction.

Examples include:

Drawing Vectors

To find the value of this resultant force, below, you have to draw these forces to scale!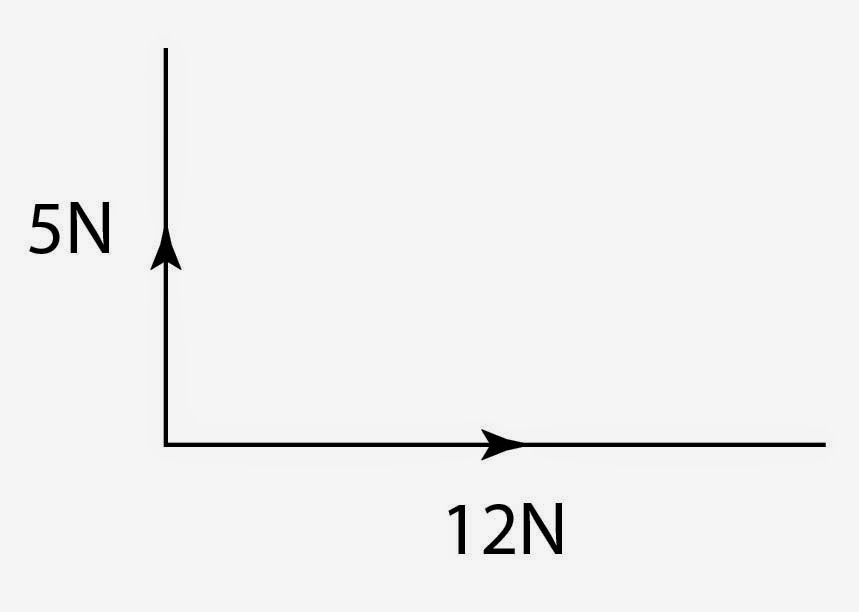

For example, the 5N might be 5cm and the 12N is 12cm.

We then draw on of the forces, say the 12N and then we draw the 5N going upwards.

You can then measure the distance between the the start of the 12N line and the end of the 5N line to get your answer. This means that you MUST bring a ruler to the exam!!

The same can be done the other way around. If you are given a diagonal line and are asked to write down the vertical and the horizontal components of the vector then draw the respective lines and measure them. Take heed of any scale factor that is given!

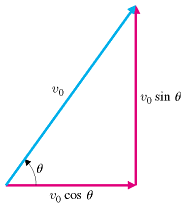
There is another method, which uses trigonometry:

This means that you can calculate the horizontal and vertical components which just the resultant force/velocity (the hypotenuse) and the angle to the horizontal.

Equillibrium

Sometimes you may be asked to show how a slightly more complicated system is in equilibrium or balanced.

This situation may have a two or three forces coming off at different angles to each other.

They key part here is to break each force into its horizontal and vertical components, add up the like components and see if your answer is zero. If so, then the forces are in equilibrium with each other.

Is momentum scalar or vector?

Vector

Is kinetic energy scalar or vector?

Scalar

Moments

Moment of Couple

Principle of Moments

Ensuring that the objects are in equilibrium is known as the principle of moments. Lets look at an example:

The weight of the object acts at the ‘centre of mass’. The centre of mass is the point where all the mass is thought to be concentrated. In a regular shape with uniform mass, the centre of mass will be located in the middle.

Motion Along a Straight Line

GCSE Motion

Velocity is a measure of the displacement an object covers in a given time frame:

v = velocity (ms-1)

s = displacement (m)

__t __= time (s)

There are two different ‘types’ of velocity you might be asked about. One is average velocity whilst the other is instantaneous velocity.

Average velocity is calculated over a long period of time and often there will include some sort of acceleration involved.

Instantaneous velocity is the velocity at one particular moment.

Acceleration is a measure of the change in velocity over time.

a = acceleration (ms-2)

v = velocity (ms-1)

t = time (s)

Motion Graphs

Motion can be depicted graphically, and the graphs contain lots of different information about the motion of an object.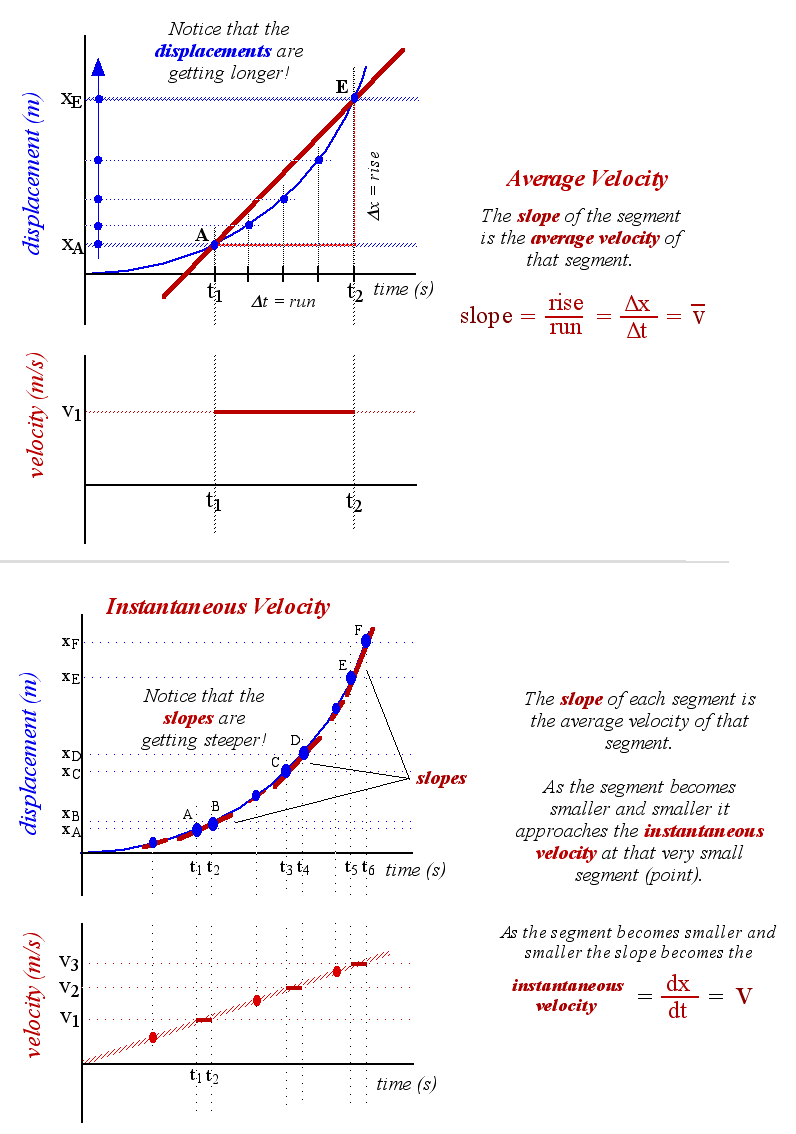

First we have a displacement time graph. The gradient of this tells us the velocity. The average velocity is calculated as shown - the gradient between the time frame required by the question which, in the general case, is t1 and t2.

This graph shows how to calculate instantaneous velocity. At a give point in time, specified by the question, you take the tangent of the line at that point. Calculate the gradient of the tangent and you have your answer.

For the velocity-time graph - acceleration is the gradient of the line. Sometimes the acceleration will not be uniform. To calculate the acceleration at a certain point you take the gradient of the tangent at that point, just like the above.

The area underneath the graph on a velocity-time graph is the displacement.

SUVAT

The SUVAT equations are used to calculate displacement, initial and final velocity, acceleration and time. You need to be very comfortable in using these equations.

Notice that each equation is different as they only have four of the five quantities of motion. Carefully reading the question and writing down the information provided will help make it clear which equation you need to use. Sometimes you may need to use two equations in the same answer.

In certain scenarios where an object is falling, the acceleration due to gravity is __g __- gravitational field strength.

Projectile Motion

Vertical and Horizontal Components

As discussed in a previous learning episode we can split a vector quantity into vertical and horizontal components. The majority of 4 mark plus SUVAT questions will involve you splitting a motion into its horizontal and vertical components and then relating relevant information between the two.

As a brief and key list of things to do; you must:

Example Past Paper Question

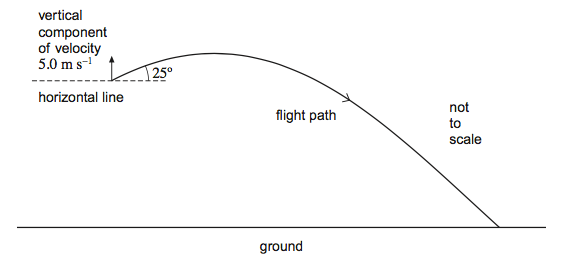
A projectile is launched some distance above the ground at an angle of 25° above the horizontal with a vertical component of velocity of 5.0 m s−1. Figure 1 shows the flight path of the projectile. The flight takes 1.3 s.

Ignore the effects of air resistance throughout this question.

Figure 1:

(a) (i) Show that the initial speed of the projectile is about 12 m s−1. (using sin 25° = VV/V -> V = VV / sin 25°)

= 5.0/sin25° ✔

11.8 (m s-1 ) ✔

(2) (ii) Calculate the horizontal component of velocity as the projectile hits the ground. (using tan 25° = VV /VH)

VH = VV /tan 25° ✔

= 5 / tan 25° =11(m s-1) ✔ (10.7m s-1)

Or (using cos 25° = VH / V )

VH = V cos 25° ✔ = 11.8 cos 25° = 11 (m s-1) ✔ (10.7 m s-1)

Or (using VH2 + VV2 = V2)

VH2 + 52 =11.82 ✔ (0r 122)

VH = 11 (m s-1) ✔ (10.7 m s-1)

__(2) (b) (i) __Calculate the maximum height above the starting point reached by the projectile. Give your answer to an appropriate number of significant figures. (using v2 = u2 + 2as with up being positive 0 = 5.02 + 2 × -9.81 × s)

s = 1.3 (m) ✔ (1.27 → 1.28 m)

or (loss of KE = gain of PE

½ m v2 = m g h

½ 5.02 =9.81 × h)

h = 1.3 (m) ✔ (1.27 → 1.28 m)

__(2) (ii) __Calculate the total horizontal distance travelled by the projectile from its starting point. (using s = (u + v)t/2) or horizontal distance = speed × time)

s = 11 × 1.3 = 14 (m) ✔ (using 10.7 gives the same answer)

(1) (c) (i) Mark with an A on the flight path in Figure 1 the position where the speed of the projectile is greatest.

A marked at the point of landing or immediately before ✔ (1)

(ii) Mark with a B on the flight path in Figure 1 the position where the speed of the projectile is least.

B marked at the maximum height of the path ✔ (1)

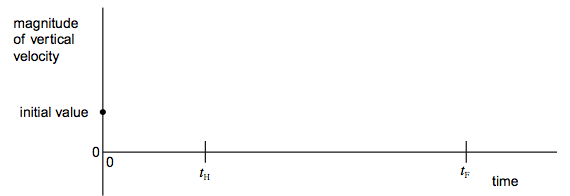
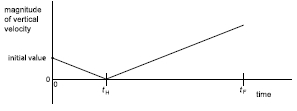
(iii) The projectile reaches its maximum height at time tH and finishes its flight at time tF. Draw on Figure 2 a graph to show how the magnitude of the vertical component of velocity of the projectile varies with time. Numerical values are not required.

Figure 2:

straight line from point given down to point tH on the axis ✔

straight line starting where first line stops (tH) but with opposite gradient to the first line ✔

(2)

(total 11 marks)

Terminal Speed

Friction is a resistive force that opposes ones motion. It occurs when an object slides over another and the constant rubbing causes a loss of energy which dissipates to the surroundings as heat.

There are a number of different frictional forces such as air resistance, water resistance etc.

Terminal speed is the maximum speed an object can reach in free fall.

It can be explained as follows:

As an object fall, it initially only has the downward force - weight - and the object accelerates at a rate equal to the gravitational field strength, g. As time continues there is a frictional force, air resistance, that acts upwards. The air resistance force increases which causes the magnitude of the acceleration to decrease. During this time the object is still increasing its speed.

At a given point the air resistance, or drag, is equal to that of the weight. At this point the resultant force is zero and there is no acceleration. The object is now moving at a terminal speed. The faster an object falls the greater the air resistance.

Air Resistance

As mentioned above, air resistance is a frictional force caused by the collision of air particles on a moving object.

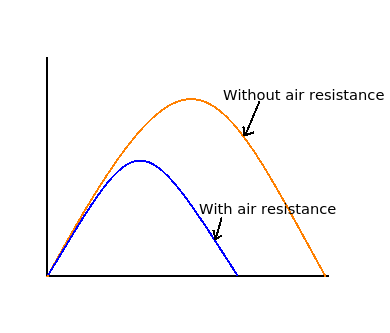
Air resistance affects both the vertical and horizontal components of an object’s velocity.

This is shown in the diagram opposite. The blue line showing a projectile with air resistance. You can clearly see that air resistance affects both components and that it does not reach the same speeds.

Newton’s Laws of Motion

Newton had three laws of motion. We will discuss each on in turn.

1st Law:

An object will remain at a constant velocity until a new force acts upon it.

This means that an object will continue to be at rest of move a constant speed until a new force changes this motion.

2nd Law:

For an object with constant mass the force on an object is directly proportional to the acceleration of the object.

This can also be written as F = ma

3rd Law:

Every action has an equal and opposite reaction.

This means that if a force from one object is exerted on another. Then the second object will exert a force of equal magnitude but in the opposite direction on the first.

A car accelerates at a rate of 5m/s2. If it weighs 500kg how much driving force is the engine applying?

Your answer should include: 2500 / 2500N

A constant force on a car is 1200N. If the car has a mass of 20kg, what is the acceleration?

60

Momentum

Conservation Law

The conservation law of momentum states that:

The total momentum in a system before a collision/incident is equal to the total momentum after the collision/incident.

Momentum = mass x velocity

This is what we already learnt from GCSE.

Here, we now include the relationship between force and momentum.

Where:

F = Force (N)

m = mass (kg)

v = velocity (ms-1)

__t __= time (s)

p = momentum (kgms-1)

This shows the rate of change of momentum.

It is clear to see that if the time of a collision is increased, the force decreases. This is important for transport safety. For example, seat belts are designed so they prolong the amount of time it takes for an incident to occur. This means that the person experiences a smaller impulse and a smaller force.

Elastic collisions occur when the objects separate after the collision. In this case, recall that velocity is a vector so one direction is positive whilst the other is negative.

Inelastic collisions occur when the objects are stuck together after the collision. In this case the masses are added into the final momentum.

Explosions occur with the momentum of the system is zero. Remember that velocity is a vector so one direction is positive whilst the other is negative.

Impulse

We can rearrange this to show that the impulse is equal to the rate of change of momentum.

Force-Time Graph

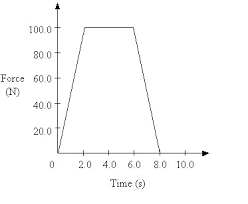
A force time graph show a graphical representation of how force and time are interlinked. The area underneath the graph represents the impulse of the system, which is also the change in momentum.

What is the momentum gained by the object from t = 0 to t = 10 s?

58

Work Energy and Power

Work and Energy

At GCSE we defined work done as Fs (force x distance) and these were done along a vertical or horizontal surface.

At A-level we now have questions which have these components combined.

Therefore the work done which is equal to the energy transferred can now be calculated as:

W = Work done (J)

F = Force (N)

s = displacement (m)

𝜃 = The angle between the horizontal and the hypotenuse.

cos𝜃 = the horizontal component

You can use sin𝜃 instead where sin𝜃 = the vertical component

For example:

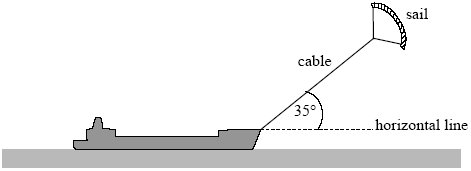
The diagram below shows a ship fitted with a sail attached to a cable. The force of the wind on the sail assists the driving force of the ship’s propellers.

The cable exerts a steady force of 2.8 kN on the ship at an angle of 35° above a horizontal line.

Calculate the horizontal and vertical components of this force.

horizontal component (= 2.8 cos 35) = 2.3 (kN) (2293.6)

vertical component (= 2.8 sin 35) = 1.6(kN) (1606.0)

horizontal component of force: 2.3kN

vertical component of force: 1.6kN

The rate at which work is done can be calculated by:

Rate of doing work = rate of energy transfer;

P = Power (W)

__W __= Work done (J)

t = time (s)

F = Force (N)

v = velocity (ms-1)

These equations and relations are very much related to the ones above. Often this will form the part .3 or .4 of a question where you will use previously calculated data in these equations.

Take a moment to see how they feed into each other and rearrange them by substituting out Force or Work Done.

Efficiency

Efficiency is a measure of how well an object outputs useful energy, compared to how much energy is taken in.

The measure is between 0 and 1, where 1 is totally efficient. This can also be measured between 0% and 100% and is done by multiplying your answer by 100.

Sometimes you will be asked to leave your answer as a decimal (first equation) and sometimes as a percentage (second question). It is important to read the question carefully to see which one it wants. If it is unspecified then you can leave your answer in either form.

Conservation of Energy

The most fundamental law of all of nature is the conservation of Energy.

This states that: Energy cannot be created or destroyed only transferred from one store to another.

This means that when energy is ‘lost’ it is actually converted into another form or store.

For example, is we have an object which is being held above the ground. It might have 10J of gravitational energy and 0J of kinetic. Once released and the object falls, the energy is the gravitational store will decrease and energy in the kinetic store will increase. This will go up until the point where the object is just above the ground. At this point there will be 0J in the gravitational store but all 10J in the kinetic store.

All the possible applications that you will be asked will involve either:

In all cases you must talk about how the energy from one has been transferred into the other. Question depending, you should also mention how the loss of energy from one affects the motion of the object.