Periodic Motion

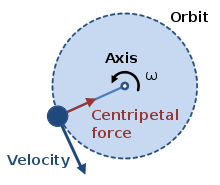
Circular Motion

Where there is an object moving in a circular path at a constant speed, there is a forever changing velocity, acceleration and a centripetal force is required.

The changing velocity and acceleration occur because these are vector quantities. Since circular motion always includes a change in direction, this causes any vector quantity to continuously change.

Centripetal force acts from the object towards the pivot that it is turning around.

Angular Speed

Angular speed, which is the magnitude of the velocity can be calculated by the following relationship.

⍵ = angular speed (ms-1)

v = magnitude of angular velocity

r = radius

2𝝿 = Angle of a full circle in radians. Note that the actual angle in a question might not be a full circle. Ensure that you can convert from degrees into radians (times by pi and divide by 180).

f = Frequency (Hz) Note that if the question gives you a time, recall that

Centripetal Acceleration

The acceleration of an object in a circle can be calculated by the following relationship:

Centripetal Force

The last relation in this section is the calculation for centripetal force:

Moving from the centripetal acceleration to the centripetal force should be easy when recalling Newton’s second law of F = ma.

Simple Harmonic Motion(SHM)

Characteristics of Simple Harmonic Motion

Simple Harmonic Motion (SHM) describes the way that oscillating objects move. Consider a spring with a mass going from side to side and a mass is mounted on a small railway truck, which is free to move from side to side.

The rest or equilibrium position at O is where the spring would hold the mass when it is not bouncing. A is the position where the spring is stretched the most, and B is where the spring is squashed most.

At A there is a large restoring force because that is where the spring is stretched most. As a result of this the mass is accelerated. It accelerates __towards __the rest position.

Its velocity to the left increases. The acceleration decreases as the mass approached the rest position and due to inertia, the mass overshoots the rest position.

Then the spring is being compressed, and there is a restoring force to the right.

At B the acceleration is at a maximum, but this time to the right.

At both A and B, the potential energy is at a maximum; the kinetic energy is zero.

As the mass passes the equilibrium position, there is zero potential energy, but maximum kinetic energy because this is the point at which the object has its greatest velocity. Therefore there is an interchange between potential and kinetic energy.

We can write down a relationship between the acceleration, a, and the displacement, x.

Since F = ma (Newton’s 2nd Law) and __F = kx __(Hooke’s law)

Then a = F/m = kx/m

So we are saying that the acceleration is proportional to the displacement from the equilibrium position. Recall that acceleration is a vector, so we must be careful of the direction. The acceleration is towards the equilibrium position.

Conditions and Equations

The conditions for SHM are that:

1. The acceleration is proportional to the displacement
2. The acceleration is in the opposite direction to the displacement

Therefore:

Some useful relationships for SHM

Generally we measure the period, which is the time taken to make a complete oscillation or cycle. The frequency is the reciprocal of the period: f = 1/T

Acceleration can be linked to displacement by: __a = - (2𝝅f )2 x __

This satisfies the condition for SHM that a = -kx; in this case k = ω2 = (2𝝅f)2.

Angular velocity is a quantity that is borrowed from circular motion. It is the angle in radians turned per second. In SHM terms, we can consider it as the fraction of a cycle per second. It can be, of course, greater than 1: ω = 2𝝅f

This can also be written as: a = - ω2 x

The velocity at any point in the oscillation given by: v2 = ω2(A2 – x2)

Thus v = ω√(A2 – x2)

In this relationship, A is the amplitude and x is the displacement from the equilibrium position. If x = 0, v has a maximum value; if x = A, v = 0. The velocity is 0 at each extreme of the oscillation.

The displacement, x, is given by: __ x = ± Acosωt__

The plus and minus sign here tells us that the motion is forwards and backwards. Which sign we give for direction is up to the individual. Generally left to right is forwards.

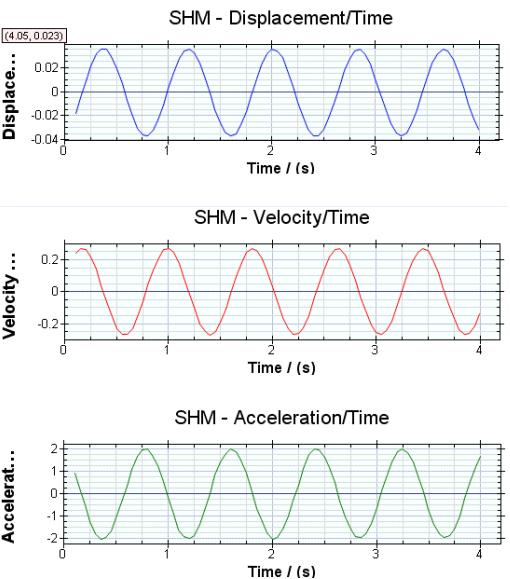
Graphical Representations

All these equations are true for any simple harmonic motion. We can show the relationships graphically by showing displacement, velocity, and acceleration against time:

These graphs are sinusoidal. The displacement is p/2 radians (900 or ¼ cycle) behind the velocity. The displacement and acceleration are p 1800 radians out of phase.

The v-t graph can be derived from the gradient from the x-t graph. The a-t graph can be derived from the gradient of the v-t graph.

The maximum speed that an object can reach is 𝜔A with the maximum acceleration being 𝜔2A

Simple Harmonic Systems

Mass Spring System

The extension of a spring is directly proportional to the force (Hooke’s Law). Consider a mass, m, put onto a spring of spring constant k so that so that it stretches by an extension_ l_.

The force on the spring = mg, and the stretching tension = k l.

        Thus mg = k _l_

Suppose the spring is pulled down by a distance x below the rest position. Now the stretching force become k(l + x).

This is also the tension in the spring acting upwards. So the restoring force,

         Fup = k(_l_ + x) – mg.

This is because mg is the weight, which always acts downwards.

Since k _l _= mg, we can write:

Fup = k l + kx – k _l _

We can now apply Newton II to write: -kx = ma (The negative sign tells us that the force is upwards)

We know from SHM that a = -𝛚2x, so we can write: a = -kx/m = -𝛚2x

So we can rearrange this to say that 𝛚2 = k/m.

Since a = -𝛚2x we can say that the condition for SHM is satisfied in this system, as long as Hooke’s Law is obeyed. Since T = 1/f, we can now write down an expression to relate the period with the mass and the spring constant. T = 2𝝅√(m/k)

Pendulum System

Consider a small bob of mass m hanging from a very light string, length l , which in turn hangs from a fixed point. If it is pulled to one side through a small angle 𝛳 it will swing with a to-and-fro movement in the arc of a circle

As weight mg is a vector, we can break it into its two components, mg cos𝛳 and mg sin𝛳.

At point A the bob accelerates with an acceleration a due to the force mg sin𝛳.

We can apply Newton’s 2nd Law to write:

-mg sin𝛳 = ma [negative sign as the force is directed to equilibrium position]

If 𝛳 is small and in radians, we can say that sin𝛳 ≈ 𝛳. This does not work for degrees. We can measure the chord OA, which is the displacement. Remember that displacement is the straight-line distance between two points. Now we can say that the displacement, x = Lsin𝛳. So we can therefore rewrite this as x = L𝛳. So now we can write:

-mg𝛳 = -mg(x/L) = ma [m’s cancel out]

thus a = -gx/L = -𝜔2x

The relationship a = -𝜔2x arises because this is a simple harmonic oscillator.

In this case 𝜔2 = g/L because the x terms cancel out.

We know that period is given by T = 1/f.

So we can write the formula linking period with length and gravity constant as: T = 2𝜋√(L/g)

Energy

There is constant interchange between kinetic and potential energy as the pendulum (or other oscillator) swings to-and-fro. If the system does not have to work against restrictive forces, such as friction, the total energy will remain constant.

Etot = Ep + Ek

We can show the variation of the energy graphically:

Now we will look at the energy with displacement:

Potential energy is highest when the oscillator is at the maximum amplitude;

Kinetic energy is highest when the oscillator

Forced Vibrations & Resonance

A forced vibration is one that is caused by a driving force. When this force is removed, then vibration will stop. The frequency is determined by the frequency of the driving force.

A free vibration occurs when a system is displaced and is left to oscillate.

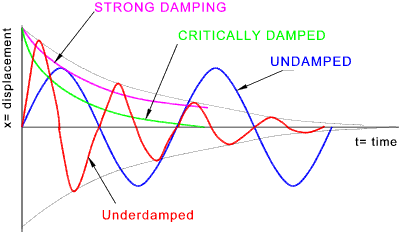
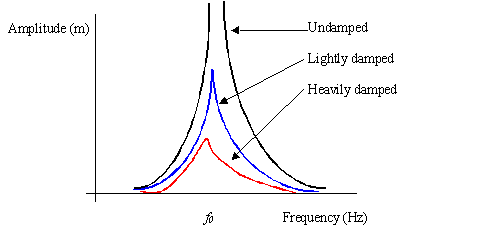
Resonance and Damping

Resonance is a special case of forced vibrations. If the forced vibrations have the same frequency as the natural frequency, the amplitude of the oscillations will get very large. This is called resonance.

Resonance can be reduced by damping. Light damping reduces oscillations slowly.

Heavy damping reduces oscillations quickly.

Critical damping stops the oscillation within one cycle. Over-damped systems do not oscillate. They take a long time to return to the equilibrium position. An example is the return spring on a door.