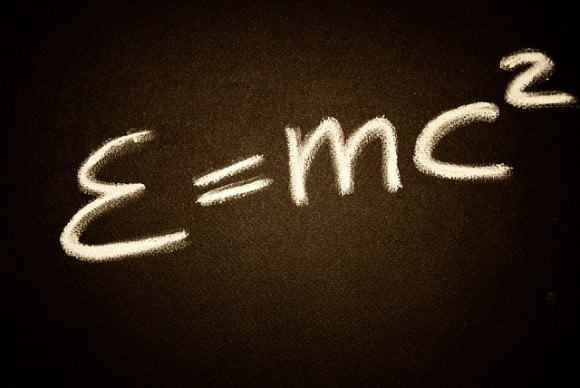Radioactivity
Rutherford Scattering
There was a major change to the atomic model by a scientist called Rutherford. This model is called the nuclear model.
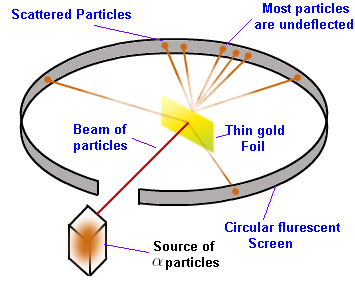
He conducted an experiment now known as the alpha particle scattering experiment (set up shown below). He fired a beam of alpha particles (Helium nuclei) at a very very thin stripe of gold foil. A number of observations led to some new conclusions and insights.
The observations and conclusions were as follows.
It was originally expected that all the alpha particles would pass through the foil without any deflections.
History of an Atom
Our understanding of the atomic model has changed throughout ages:
At first, before the discovery of the electron there was Dalton’s model. Here, atoms were thought to be tiny spheres that could not be divided.
The discovery of the electron forced an update in the model. The new model was developed by a scientist called Thomson, but the model itself is often called the plum pudding model.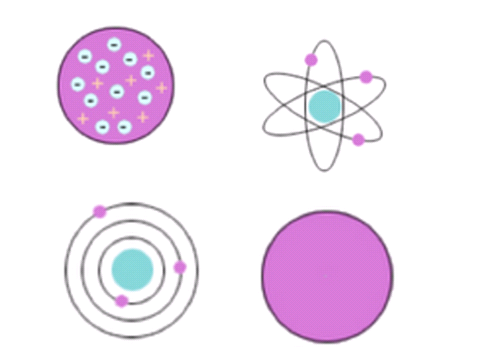
This model suggested that an atom was a sphere of positive charge with negative electrons embedded within.
After this came the nuclear model, see above.
Not long after the nuclear model, another scientist (Bohr) and student to Rutherford, updated the nuclear model. He calculated that electrons do not orbit the nucleus like planets around the sun, rather electrons orbit at very specific distances from the nucleus. These distances were known as different energy shells.
Radiation
Radioactive Decay
There are three different types of nuclear radiation that we are interested in:
Alpha (𝞪), beta (𝞫) and gamma (𝞬)
An 𝞪 particle is made up of two protons and two neutrons. It is a helium nucleus and therefore has no electrons.
A 𝞫 particle is an electron, originating from the nucleus.
𝞬 radiation it a high energy electromagnetic wave. These have really short wavelengths and high frequencies.
𝞪 particles have a range of 3-8cm in air - the shortest of the three.
They cannot penetrate skin or paper and they have the largest ionisation power of +2 (this comes from its charge.
𝞫 particles have a range of 1-5m in air - the second furthest.
They cannot penetrate a sheet of aluminium and they have an ionisation power of -1.
𝞬 radiation can travel infinitely as it is just an electromagnetic wave.
It can be stopped by thick lead and it has an ionisation power of 0.
Alpha particles are used in smoke detectors. This is useful since they are easily ionising and then cease to be alpha particles. If there is smoke in the detector the alpha particles are ionised, the drop of alpha particles is detected and an alarm is sounded.
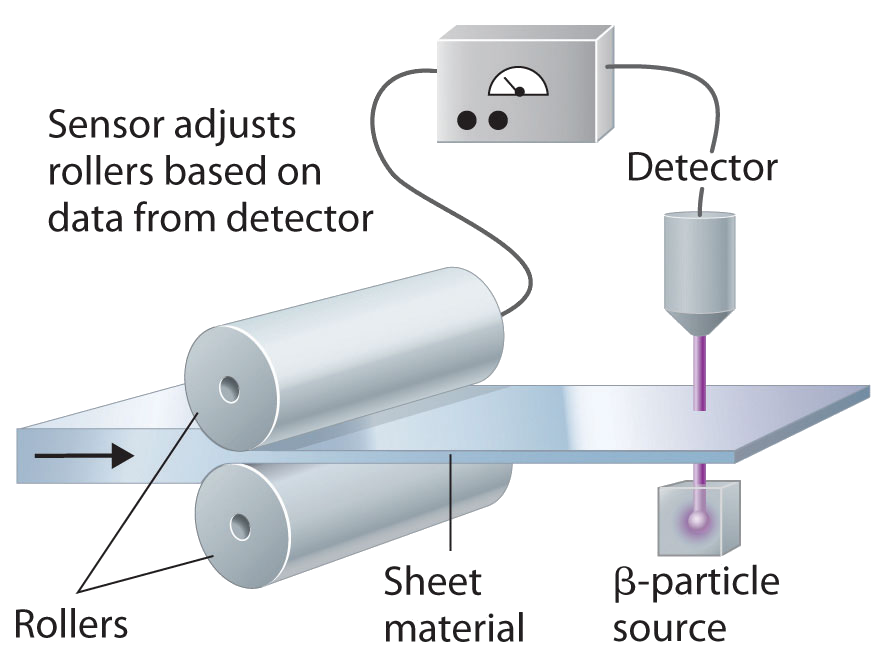
Beta particles are used to measure the thickness of paper.
If the paper is too thick then too few beta particles will be absorbed. The pressure from the rollers is adjusted to that the paper comes out thinner. Similarly, if the paper is too thin then too many beta particles reach the detector and the rollers are adjusted accordingly.
Gamma radiation is used in numerous circumstances. We use it to treat and cure cancer as well as to clean and sterilise medical equipment and food.
Inverse Square Law
We have met the inverse square law a few times from fields. The principle applies to the radiation intensity as well.
I = Intensity
k = Constant
x = distance
Applications
It is always extremely important to handle radioactive sources as the consequences can be lethal. Here is a small list of safety precautions that can be taken:
Background Radiation
There is radiation that is all around us that can be detected. This occurs even when there is no source in the room. Sources of background radiation can originate from:
The amount should normally be constant but it does vary from location to location. This is because there are some places where there is a larger collection of radioactive gas and rocks in the ground. If there have been nuclear fallouts or tests then the surrounding area will also have a higher background radiation count.
Radioactive Decay
Radioactive Decay
Radioactive decay is an entirely random process. We cannot predict when and which atoms in a radioactive sample are going to decay. We only know that they will decay at some point in the future. We can assign a probability to this and form the relation that:
N = Number of nuclei
__t __= time
𝛌 = radioactive decay constant
Activity Rate
We can then use this to determine the activity of a sample by having:
A = Activity rate (Bequerel or Bq)
1 Bq = 1 count per second
Over a longer period of time, this relationship does not hold and another relationship is used (shown by calculus and not relevant for the course).
No is the original number of nuclei in the sample.
Instead of number of nuclei, we can also do this for activity rate:
Half Life
The half life is the amount of time it takes for the activity rate to fall to half of its original value. This can be phrased another way saying it is the time taken for the sample count to fall to half of its original value.
We can relate the half-life to the decay constant:
By definition
The formula is N = N0e – λ t. Rearranging gives us
T½ is the symbol for the half life. Rearranging the above equation for T½ , so this is when the count rate/number of nuclei is half, we arrive at:
Example A radiographer has calculated that a patient is to be injected with 1 x 1018 atoms of iodine 131 to monitor thyroid activity. The half-life is 8 days. Calculate:
(a) the radioactive decay constant
(b) the initial activity
(c) the number of undecayed atoms of iodine 131 after 24 days.
(d) The total activity after 3 days.
(a) We need to use _T½ =_ __ln2
λ
we need to convert the 8 days into seconds.
λ= 0.693 \_ = __1.00 x 10-6 s-1__
8 x 86400
(b) Use Δ_N_ = - λ_N_ = 1.00x 10-6 s-1 x1 x 1018 = 1 x 1012 Bq
Δ_t_
(c) 24 days is 3 half-lives. Therefore the number atoms remaining undecayed is 1/8 of the original.
_N _ = 1 x 1018 x 8 = 1.25 x 1017
(d) 3 is not so easy. We use A = A0e – λ t
A = 1 x 1012 Bq x e-(1.00 ´ 10-6 s-1 ´ 3 ´ 86400s)
A = 1 x 1012 Bq x e-(0.2592)
= 1 x 1012 Bq x 0.772 = 7.72 x 1011 Bq.
Application
Radioactive decay has a number of uses and applications.
Medical uses of radioisotopes
Radioisotopes are widely used in medicine
• Gamma radiation from a cobalt-60 source is used to destroy deep-seated cancerous tumours. The gamma rays are concentrated on the tumour.
• Less penetrating beta radiation from phosphorus-32 can be used to treat skin cancer by direct application to the affected area.
• Radioisotopes can be used a ‘tracers’ used to monitor the processes occurring in different parts of the body. One such tracer is Iodine-131, which is taken up by the thyroid gland and can be used to monitor the workings of the thyroid.
Industrial uses of radioisotopes
• The very penetrating gamma radiation from a Cobalt-60 source can be used to inspect metal for cracks which would be invisible to the naked eye. This technique is widely used to test aircraft components for cracks caused by metal fatigue. A photographic plate is used to show any cracks - the gamma rays will be to penetrate more easily where there is a crack and so it will show up as a darker area on the photographic film.
• Leaks in gas and oil pipelines can be detected by using radioactive ‘tracers’ in the pipeline.
• The thickness of sheet material such as paper, thin metal and plastics can be automatically controlled using a beta emitter and detector. For thicker metals a gamma source would be used. If the sheet thickens the amount of radiation will fall and a signal will be sent to the rollers to move closer together until the radiation level rises to the correct reading.
Carbon dating
Carbon-14 dating can be used on material which was living in the last few tens of thousands of years, and which got its carbon from the air. Carbon 14 is a radioactive isotope of carbon. It is produced in the upper atmosphere by radiation from the sun. (Specifically, neutrons hit nitrogen-14 atoms and transmute them to carbon.)
Land plants, such as trees, get their carbon from carbon dioxide in the air. So, some fraction of their carbon is C14. The same is true of any creature that gets its carbon by eating such plants. We can measure this in living things today.
Nuclear Radius
Radius Size
The size of a nuclear radius can be calculated by the following relation:
R = Nuclear radius (m)
R0 = A constant
A = Number of nucleons
Nuclear Density
To calculate nuclear density, we can use the following relation:
This equation assumes that the nucleus is spherical, there are no gaps between the nucleons and that all nucleons have the same density.
Mass and Energy
It has been shown that energy and mass are proportional to each other. This can be shown by this, rather famous, relationship:
Fission and Fusion
Fission occurs when a nucleus splits into smaller pieces, this process also releases lots of energy. It rarely happens spontaneously and is often induced.
We can induce fission in large nuclei such as uranium-235. The most common isotope of uranium, U-238, does not split easily, but the 235 isotope does. We induce fission by “tickling” the nucleus with a _“thermal” _neutron. A thermal neutron has little kinetic energy and are in thermal equilibrium with the moderator (Graphite). This is done so that the thermal neutrons interact with the fuel and cause fission. The moderator decreases the speed of the neutron via collisions. In a reactor there are control rods (Boron) which absorb the neutrons. The neutron has to have the right kinetic energy:
• Too little kinetic energy means that the neutron will bounce off the nucleus;
• Too much kinetic energy means that the neutron will go right through the nucleus
The nucleus flies apart into a number of fragments, leaving three neutrons left over. These too are able to tickle other nuclei and make them split. Each neutron spawns two or three more neutrons in each fission, so we get a chain reaction. There is a mass defect in the products of the fission so energy is given out. In an uncontrolled chain reaction, the energy is given out in the form of a violent explosion.
Fusion occurs when two small nuclei fuse or join together to make one larger nucleus. This also gives out a lot of energy, in fact more than fission.
Each nucleus has to have sufficient energy to:
• Overcome electrostatic repulsion from the protons;
• Overcome the repulsive strong force which is found outside the region of the strong force.
This means that the gases have to be heated to a very high temperature, 100 million Kelvin
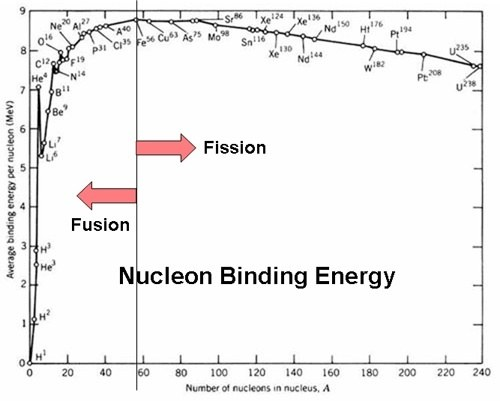
Graph
This graph shows the average binding energy along with where fission and fusion takes place. The change is at Iron, at this point more energy is required to be put into the system for fusion to occur and as such does not happen naturally.
Nuclear Instability
RadiusSize
The size of a nuclear radius can be calculated by the following relation:
R = Nuclear radius (m)
R0 = A constant
A = Number of nucleons
Nuclear Density
To calculate nuclear density, we can use the following relation:
This equation assumes that the nucleus is spherical, there are no gaps between the nucleons and that all nucleons have the same density.