Analysing Circuits

In the last couple of lessons we have learned about current, potential difference (voltage) and resistance in series and parallel circuits. Students tend to start finding circuits difficult when these three things are combined so we’ll work through some examples in this lesson so you can get the hang of it.

Any circuit problem can be solved by using a combination of Ohm’s law, the current laws and the voltage laws.

Ohms law:

voltage = current x resistance

__Current laws: __

Current is constant in a series circuit

Current divides down the branches of a parallel circuit

Voltage laws:

Voltage is shared between components in a series circuit

Each branch of a parallel circuit receives the same voltage as the power supply

Worked Examples

Worked Example 1

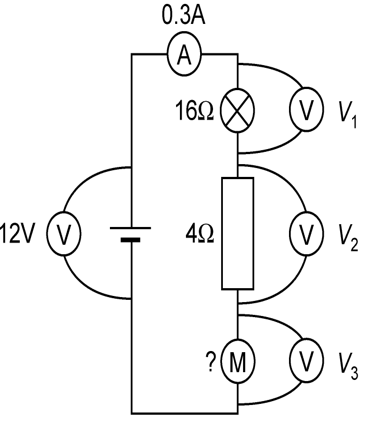
Calculate the voltmeter readings and the resistance of the motor

Steps to answer this question:

Work out whether you are dealing with a series or parallel circuit – in this case we have a SERIES circuit (the voltmeters don’t count as part of the circuit.
Voltage 1: We want to use the equation V=IR
In a series circuit, the current is the same everywhere in the circuit, so we know that the current flowing through the bulb is 0.3A
The resistance of the bulb is labelled as 16Ω
V = IR = 0.3 x 16 = 8V
Voltage 2: We want to use the equation V=IR
In a series circuit, the current is the same everywhere in the circuit, so we know that the current flowing through the resistor is 0.3A
The resistance of the resistor is labelled as 4Ω
V = IR = 0.3 x 4 = 2V
Voltage 3: We want to use the equation V=IR but we do not have enough information to use it for this voltmeter – we know the current, but the resistance has not been labelled.
At this stage, DON’ PANIC! If we can’t use the equation, there must be another way
The voltage law for series circuits says that the voltage supplied by the battery will be shared out between the components. Because we know the voltages of the other two components (and the power supply) we can work out V3
V(battery) = V1 +V2 +V3
12 = 4.8 + 1.2 + V3
V3 = 6V
Resistance of motor
Rearrange V = IR to R = V/I
R = 6/0.3 = 20 Ω

Don’t panic and work your way through Ohm’s law and the current and voltage laws until you have all the information you need.

Worked Example 2

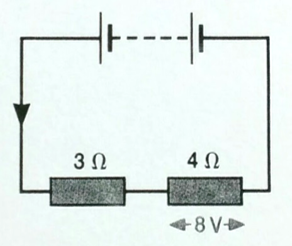
In the circuit shown, the potential difference across the 4Ω resistor is 8V

What is the current through the 4 Ω resistor?

Rearrange the equation V=IR to I=V/R

I = 8/4 = 2A

What is the current through the 3 Ω resistor?

We do not know the voltage across the 3 Ω resistor so cannot use the equation.

We do know that this is a series circuit, and in a series circuit, current is the same everywhere in the circuit.

As we have just calculated in part (a), the current through the other resistor is 2A, therefore the current through this resistor (and anywhere else in the circuit) is 2A

What is the p.d. across the 3 Ω resistor?

Use the equation V=IR

V = IR = 2x3 = 6V

What is the p.d. of the battery?

We do not know the resistance of the battery so cannot use the equation.

We do know that this is a series circuit and, in a series circuit, the potential difference (voltage) of the power supply is shared between the components.

As we know the voltages across each resistor, we can simply add those together.

V(battery) = 6 + 8 = 14V

Remember: