Turning Forces and Pressure
Moments
A moment is a turning force. The size of a moment can be calculated using this equation (you DO need to remember this equation for your exam):
Moment = force x distance from pivot
The moment can be increased by:
- Increasing the size of the force
- Increasing the distance from the pivot
Objects will balance if the clockwise moment equals the anticlockwise moment.
For an object in equilibrium (you do NOT need to remember this equation for your exam):
W1d1__ = W__2d2
W = weight (force) (N)
d = distance from pivot (m)
Worked Example
What force is needed at A to balance the beam?
Clockwise moment = 6 x 4 = 24Nm
Anticlockwise moment = 8 x 2 = 16Nm
For beam to balance, anticlockwise moment must be 24Nm
Moment at A must be 8Nm (16 + 8 = 24Nm)
Force A = moment ÷ distance
Force A = 8 ÷ 4 = 2N
Centre of Mass
Equilibrium - An object is in equilibrium when the opposing forces on it are balanced.
Centre of mass - The point on an object through which the weight of the object acts.
For a regular, symmetrical shape with its mass evenly distributed, the centre of mass will be in the middle of the object:
If the mass is not evenly distributed, the centre of mass will not be in the centre of the object:
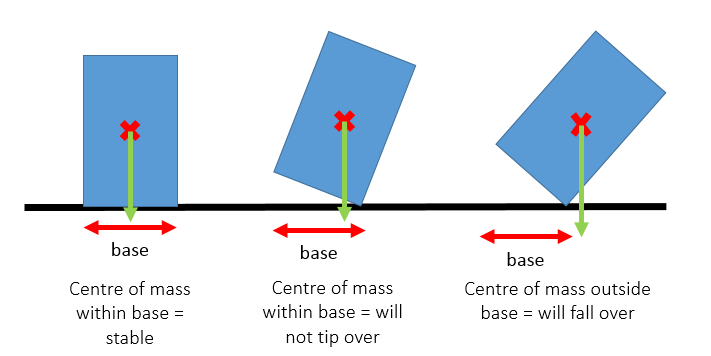
An object will balance at its centre of mass.
An object will always come to rest with its centre of mass vertically below the point of suspension.
An object will fall over if it’s centre of mass moves outside the area of its base:
Levers
A lever is a simple machine that uses moments (turning forces) to make a task easier.
There are two factors that can affect the lever:
- The force applied to it (effort)
- The distance from the pivot
There are two types of lever:
- Force multiplier - A small effort can be used to move a large load, but has to move a greater distance
- __Distance multiplier __- A small movement of the effort results in a large movement of the load, but a larger force has to be used
Example:
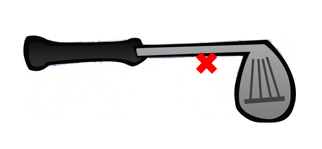
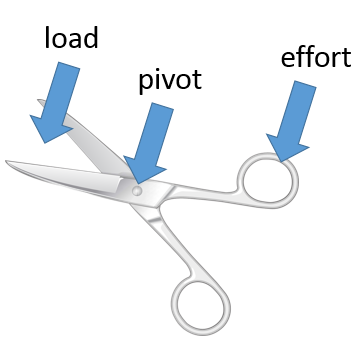
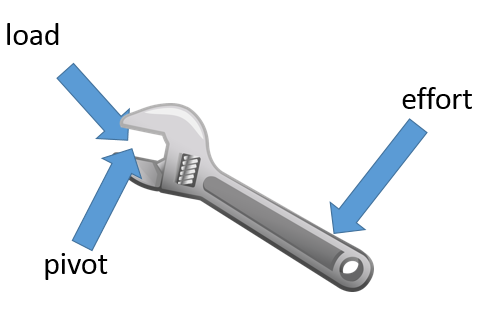
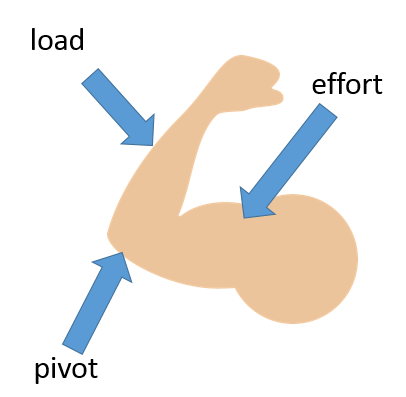
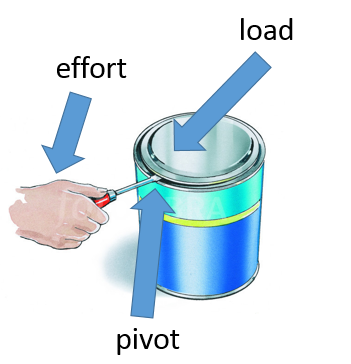
The applied force is further away from the pivot than the exerted force. This means the force exerted will be greater than the force that was applied
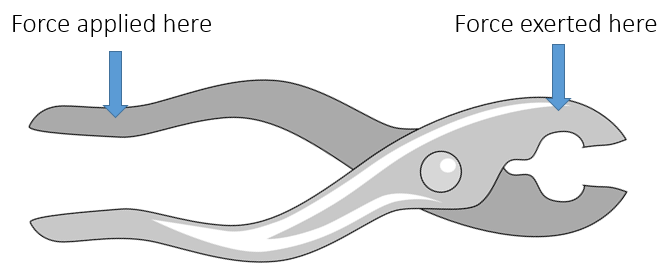
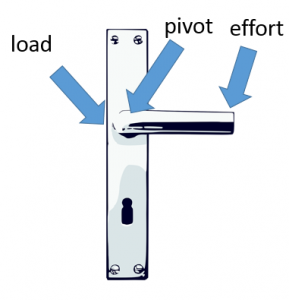
You should be able to identify the effort (input force), pivot and load (output force) are for a variety of examples of levers:
Gears
Gears multiply the effect of a turning force
Low Gear:
- Small wheel used to turn large wheel
- Low speed, high turning force
High Gear:
- Large wheel used to turn small wheel
- High Speed, low turning force
Worked Example
A gear wheel of radius 30mm is used to turn another gear wheel of radius 15mm with a force of 90N
Calculate the moment of the force on:
- The 15mm wheel
- The 30mm wheel
a)
Moment = force x distance from pivot
(distance from pivot = radius of gear wheel)
Moment = 90 x 15 = 1350 Nmm (or 1.35Nm)
b)
Moment = force x distance from pivot
(distance from pivot = radius of gear wheel)
Moment = 90 x 30 = 2700 Nmm (or 2.7Nm)
Pressure in Liquids
Pressure in liquids increases with depth. If a container of water has three holes in the side, the water will shoot out further from the lowest hole because the pressure is greatest at the bottom of the container.
Pressure in liquids also depends on the density of the liquid. The relationship between pressure, density and depth can be shown by this equation (you do NOT need to remember this equation for the exam):
p = hρg
p = pressure (Pa)
h = height (m)
ρ = density (kg/m3) **be careful as this looks a lot like p!**
g = gravitational field strength (N/kg)
Worked Example
Calculate the pressure of sea water (density 1050 kg/m3) at a depth of 100m. (g = 9.8 N/kg)
pressure = hρg
pressure = 100 x 1050 x 9.8
pressure = 1,029,000 Pa
Pressure
Surface Pressure
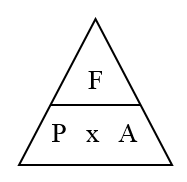
Pressure is a force acting on an area. Pressure can be calculated using the following equation (you DO need to remember this equation for your exam):
Pressure = Force ÷ Area
Pressure is measured in Newtons per square metre (N/m2) or Pascals (Pa)
The larger the force the greater the pressure.
The larger the area the lower the pressure.
Snow shoes can make it easier to walk on snow because they have a larger surface area than a normal shoe. This means that the weight of the person is spread out over a greater area of snow, meaning less pressure is applied to the snow. Therefore, the person will not sink into the snow as much, making it easier to walk
Worked Example
Volume
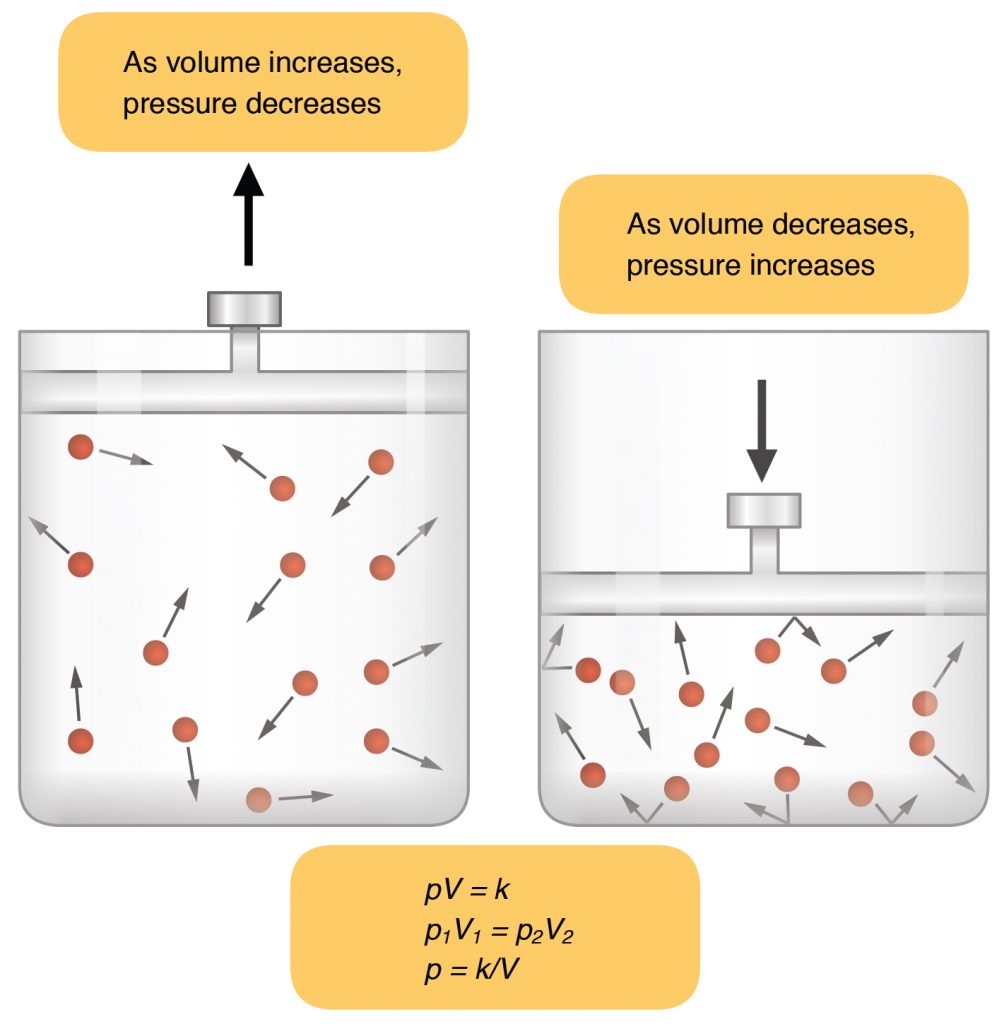
The smaller the volume, the greater the pressure. The same amount of air molecules in a smaller volume will exert more pressure as there will be more collisions.
Gas Pressure
- Atmospheric pressure is due to air molecules colliding with surfaces.
- Each collision exerts a tiny force on a surface but there are billions of collisions each second.
- Pressure can be changed by
- Changing the volume for the same amount of air (eg compressing)
- Changing the temperature
- Changing the number of air molecules (eg sucking air out of a container)
Density
Reducing the density of air particles in a container (sucking air out) will reduce the pressure in the container as there are less collisions.
A lower in pressure inside the container will mean that here is a larger force being applied outside the container, which could result in crushing the container.
Video - Crushing steel drum
Temperature
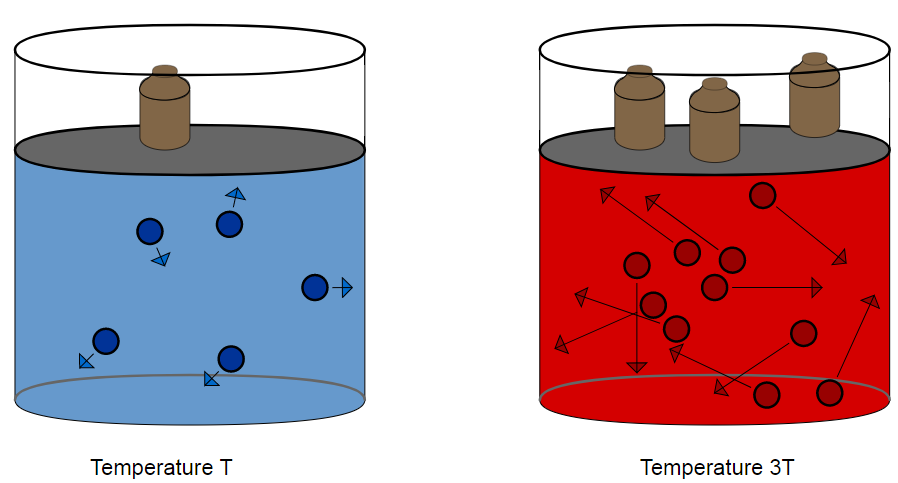
The higher the temperature, the greater the pressure. Increasing the temperature of a gas will increase the pressure as the particles move faster, causing more frequent collisions.
Altitude
Atmospheric pressure changes with height above sea level. The higher the altitude, the lower the pressure.
The equation linking altitude and pressure is the same as the fluid pressure equation (you do NOT need to remember this equation for the exam):
p = hρg
p = pressure (Pa)
h = height (m)
ρ = density (kg/m3) **be careful as this looks a lot like p!**
g = gravitational field strength (N/kg)
A difference in pressure between two areas will cause a force to be exerted on the barrier between them. For example, the air pressure inside an aeroplane flying at 30,000ft is much higher than the air pressure outside the plane. This means that a force is exerted on the windows, doors and walls. The plane needs to be built to withstand these forces.
The size of the force can be calculated using this equation (you do NOT need to remember this equation for your exam):
F = ∆p x a
F = force (N)
∆p = pressure difference (Pa)
a = area (m2)
- What moment is caused by a force of 5N acting 4m from the pivot?
- Your answer should include: 20Nm / 20
Explanation: 20Nm - A boy of weight 40N is sitting 0.5m away from the pivot of a see-saw. How far away from the pivot on the other side would a girl of weight 25N need to sit in order to balance the see-saw?
- Your answer should include: 0.8m / 0.8
Explanation: 0.8m - A box has a weight of 180N and a base of area 0.09m2. What pressure does it exert on the ground?
- Your answer should include: 2000Pa / 2000
Explanation: 2000Pa - Calculate the pressure exerted by a concrete slab of area 20m2 with a weight of 160,000N.
- Your answer should include: 8000Pa / 8000
Explanation: 8000Pa - A plug with an area of 0.005m2 is used in a bath which is filled with water to a depth of 0.4m. Calculate the pressure on the plug due to the water.
- Your answer should include: 3920Pa / 3920
Explanation: 3920Pa