Newton's Laws of Motion
Newton’s Laws of Motion
Forces can be categorised as contact or non-contact forces:
Contact Force - The objects are touching, i.e.:
- Friction
- Air resistance
- Tension
Non Contact Force - The objects are not touching, i.e.:
- Gravity
- Magnetism
- Electromagnetism
Newton’s 3rd Law of Motion
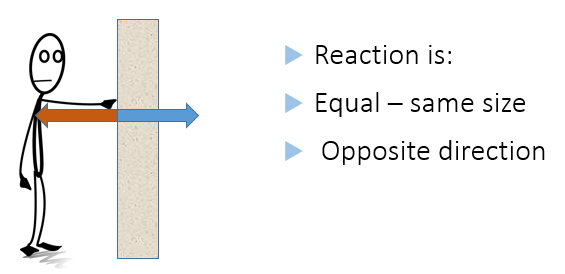
Every action has an equal and opposite reaction
For example, if you push against a wall, the wall must be producing an equal and opposite force on you otherwise the wall would fall over or your hand would go through the wall.
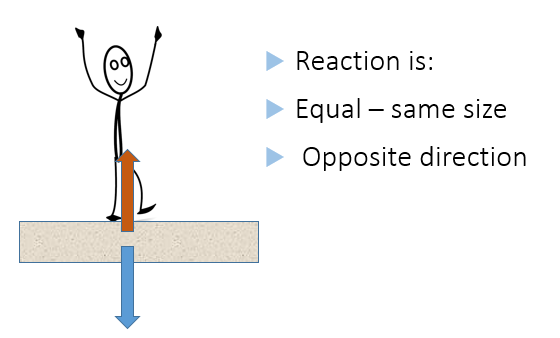
Gravity is pulling you down towards the centre of the earth but, at this moment you are (probably) not moving down through the floor. This is because the floor exerts an equal and opposite force on you, holding you up.
Other examples include:
The recoil force on a gun (the gun recoils back to the shooter as the bullet is fired)
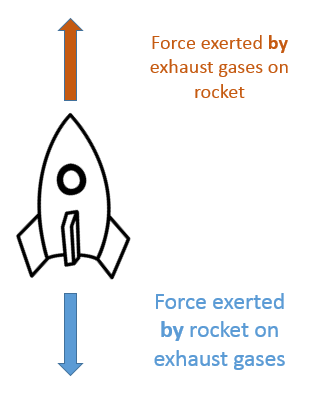
Exhaust gases used to provide thrust for a rocket
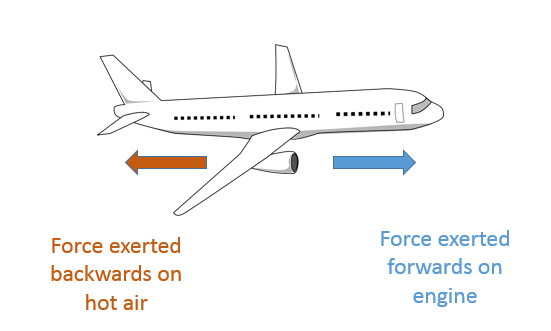
Jet engines
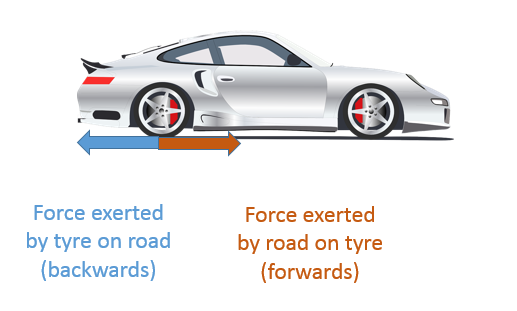
Car tyres
If a car is driving on softer ground, such as mud, the wheel still exerts a force on mud backwards. However, the mud is unable to produce a reaction force to push the car forwards. Therefore the wheels spin and spray mud backwards but the car does not move forwards.
Newton’s 1st Law of Motion
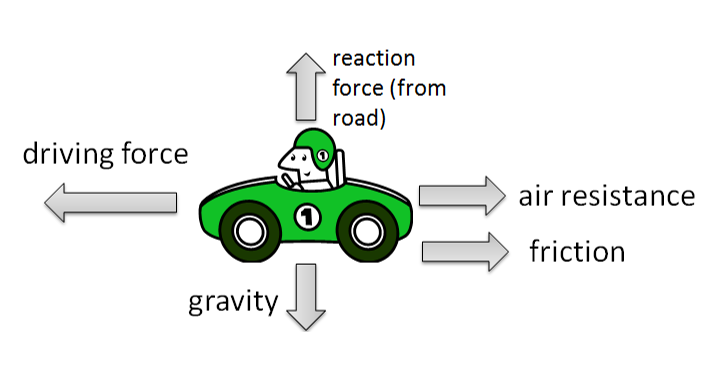
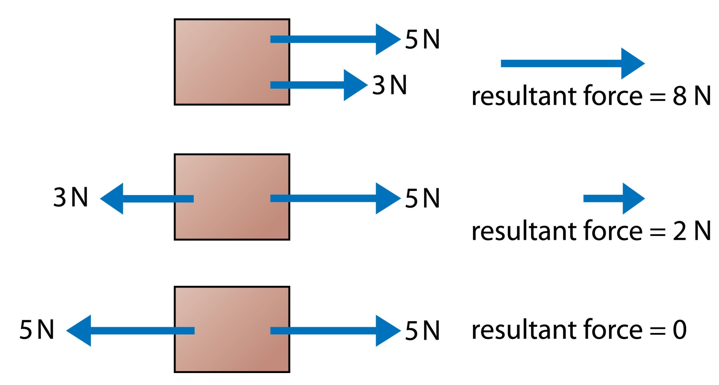
On any object, there are usually multiple forces acting.
The resultant force is the sum of all the forces acting on an object.
Newton’s 1st law of motion states that an object will stay at rest, or continue at a constant speed, unless it is acted on by an unbalanced force.
This means:
- Balanced forces = no change in motion (this could mean the object is not moving OR that it is moving at a constant speed)
- Unbalanced forces = change in motion (this could be speeding up, slowing down or changing direction)
For example, the reason you are thrown forwards in a head-on collision is that objects continue in their current state (rest or constant speed) unless acted on by a resultant force. Therefore, your body will continue moving forwards until it experiences a force slowing it down (eg from the road ahead).
If an astronaut throws an object in space it will continue moving at a constant speed because there is no air resistance to slow it down. If you throw the same object on the Earth, air resistance slows it down and gravity pulls it to the ground where it then experiences friction, bringing it to a stop.
Gravity
- Mass - The amount of matter in an object. Measured in kilograms (kg)
- Weight - The force on an object due to gravity. Measured in Newtons (N)
- Gravity – The force of attraction between objects
For example, the mass of an astronaut is the same whether on the Earth, the moon or in outer space because there is the same amount of matter in the body of the astronaut. However, his weight is different in those locations because of the different gravitational field strength.
The relationship between mass, weight and gravity is described in this equation (you DO need to remember this for your exam):
W = mg
W = weight (N)
m = mass (kg)
g = gravity (N/kg)
Newton’s 2nd Law of Motion
Newton’s 2nd law applies to objects that have a resultant force acting on them (and so their motion is changing)
The acceleration of an object is directly proportional to the force acting on it, and inversely proportional to it’s mass.
- Bigger force = bigger acceleration
- Bigger mass = smaller acceleration
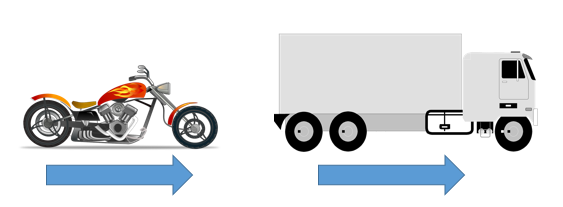
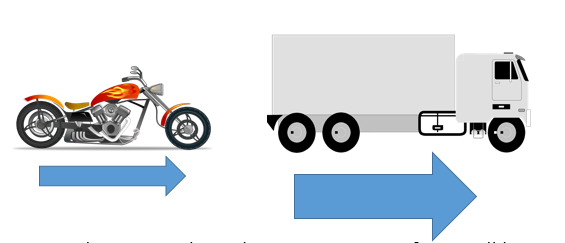
For example, if the same force is applied to these vehicles, the motorbike will accelerate faster due to its smaller mass.
Or, to achieve equal acceleration a greater force will be needed for the truck due to its larger mass.
Newton’s 2nd law is often represented by an equation (you DO need to remember this equation in your exam).
F = ma
F = force (N)
__m __= mass (kg)
a = acceleration (m/s2)
Worked Example
Calculate the resultant force on an object of mass 6kg when it has an acceleration of 3m/s2
- F = ma
- F = 6 x 3
- F = 18N
- A car accelerates forwards. What direction is the force that the car exerts on the driver?
- forwards
- A car accelerates forwards. What direction is the force that the driver exerts on the car?
- backwards
- What force is required to accelerate an object of 3kg at 2m/s2?
- Your answer should include: 6N / 6
- What is the weight of an object of mass 15kg on the Earth (gravitational field strength 9.81 N/kg)?
- Your answer should include: 147.15N / 147.15
- What is the mass of an object that weighs 70N on the moon, where the gravitational field strength is 1.6N/kg?
- Your answer should include: 43.75kg / 43.75
Terminal Velocity
As an object falls, it’s speed changes due to the changing forces acting on it.
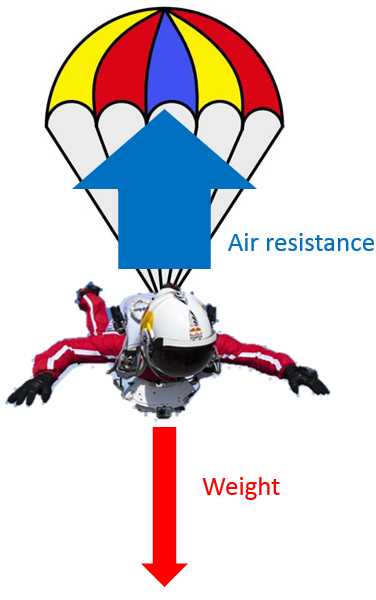
At first the weight is greater than the air resistance and so the sky-diver speeds up.
The faster the sky-diver gets, the bigger the force of air resistance becomes because there are more collisions with air particles (the weight remains constant throughout the fall)
Eventually, the air resistance equals the weight. The forces are now balanced so the sky diver continues falling at a constant speed. This maximum speed is known as terminal velocity.
When the sky-diver opens the parachute, the air resistance increases dramatically and is greater than the weight. This unbalanced force slows the sky-diver down.
As the sky-diver slows down, the air resistance decreases as there are less collisions with air particles taking place. Eventually, the air resistance equals the weight again and the forces are balanced. The sky-diver will continue at a constant speed (which is a lower speed than before the parachute is opened).