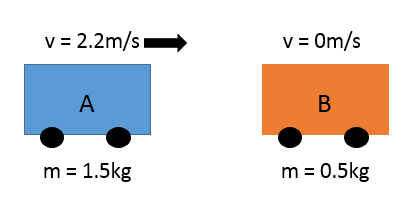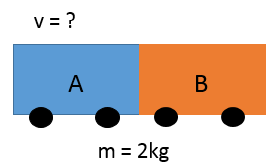Motion

Speed and Acceleration

Speed (scalar): The distance covered per unit of time

Velocity (vector): Speed in a given direction

Velocity (or speed) can be calculated using this equation (you DO need to remember this equation in your exam):

s = vt

s = distance (m) **be careful here as it is easy to assume ‘s’ stands for speed!**

__v __= velocity (m/s)

__t __= time (s)

Acceleration can be calculated using this equation (you DO need to remember this equation in your exam):

a = Δv ÷ Δt

a = acceleration

Δv = change in velocity

Δt = change in time

Acceleration is measured in m/s2

Worked Example

A bus accelerates from 5 m/s to 25 m/s in 10s. What is it’s acceleration?

∆v = 25 – 5 = 20m/s

∆t = 10s

A = 20 ÷ 10 = 2 m/s2

Acceleration can also be calculated using this equation (you do NOT need to remember this equation in your exam):

v2 – u2 = 2as

v = final velocity

u = initial velocity

a = acceleration

s = distance

Worked Example

A bus accelerates from 5 m/s to 25 m/s in 10s. How far does it travel during this time?

a = 2 m/s2 (from ∆v ÷∆t)

v2 - u2 = 2as

s = (v2 - u2) ÷ 2a

s = (252 – 52) ÷ 4

s = 150m

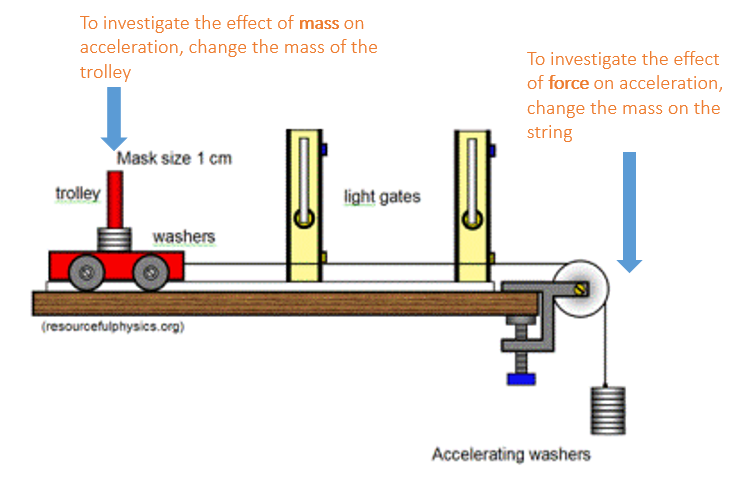
Required Practical – Acceleration

You need to be familiar with the method used to investigate the effect of force (or mass) on the acceleration of an object.

Motion, figure 1

If you are investigating force, then the number of masses on the end of the string should be changed but the mass of the trolley should remain constant.

If you are investigating mass, then the number of masses on the trolley should be changed but the mass on the end of the string should remain constant.

Examples:

Video 1

Video 2

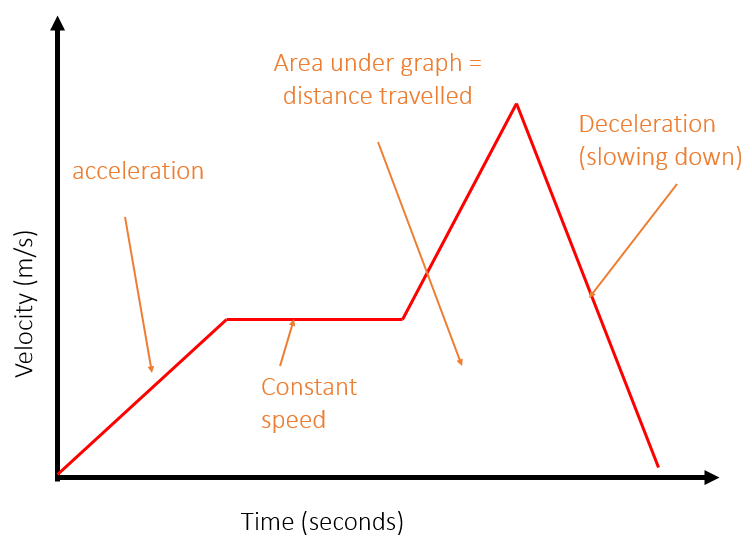
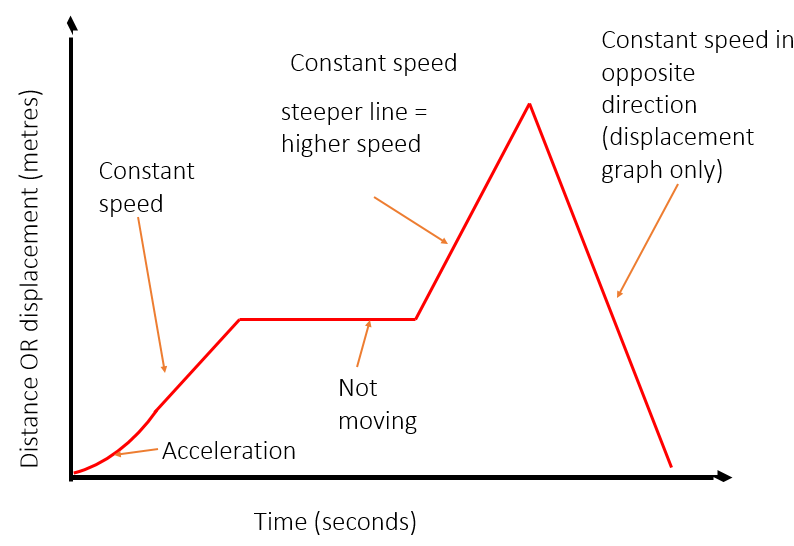
Velocity-Time Graphs

A velocity-time graph can look very similar to a distance-time graph but it represents different motion, so make sure you check the axes of the graph on any question so you know which one you are dealing with.

Motion, figure 1

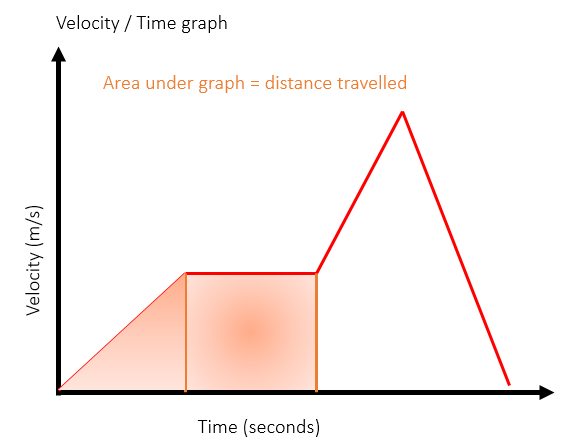
To calculate the distance travelled during a section of a velocity-time graph, calculate the area under that section of the graph

Motion, figure 2

Momentum

Momentum can be calculated using the following equation (you DO need to remember this for your exam):

p = mv

__p __= momentum (kgm/s)

m = mass (kg)

v = velocity (m/s)

With momentum (and velocity), + and – signs are used to indicate direction. For example, a car travelling with a momentum of -100kgm/s has the same momentum as a car with 100kgm/s but it is travelling in the opposite direction.

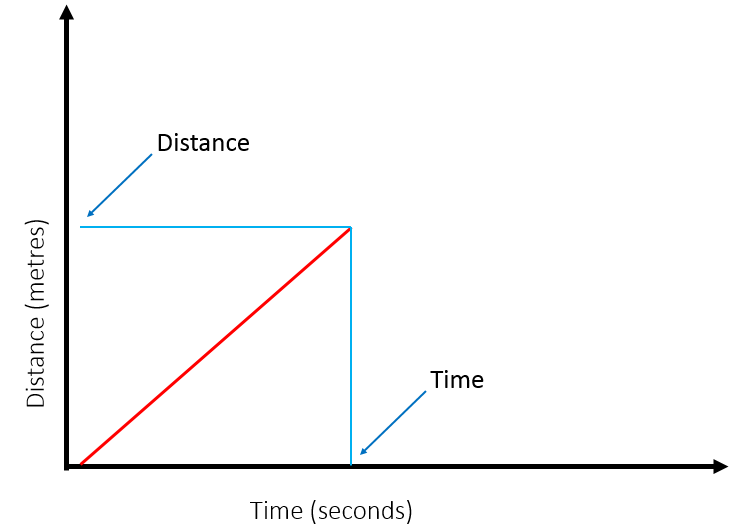
Distance-Time Graphs

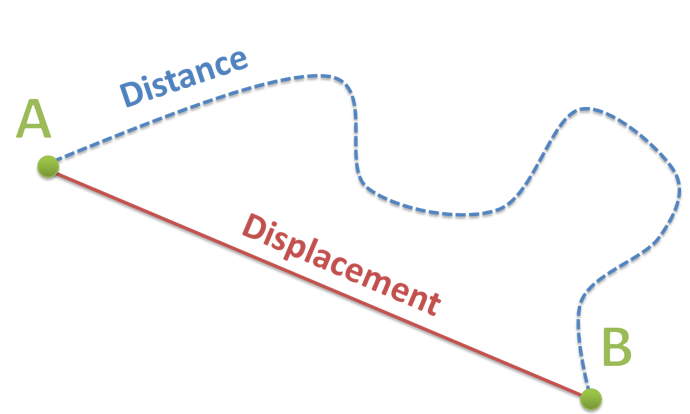
Distance (scalar): How much ground an object has covered during its motion

Displacement (vector): The overall change in position of an object

Motion, figure 1

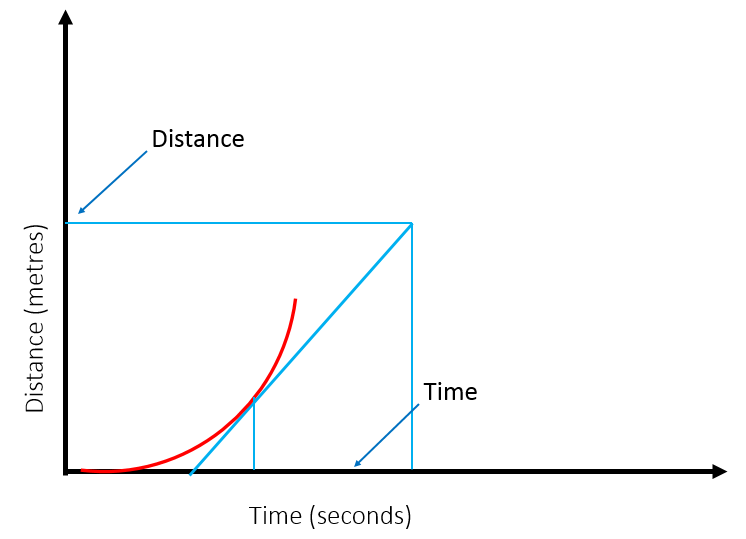
You need to be able to interpret the shape of a distance-time graph

Motion, figure 2

To calculate the speed from a distance time graph, work out the gradient of the line

Motion, figure 3

To calculate the speed during a period of acceleration, draw a tangent to the curve and calculate the gradient of the tangent

Motion, figure 4

Momentum

Typical speeds:

  1. Walking 1.5m/s
  2. Running 3m/s
  3. Cycling 6m/s
  4. Sound 330m/s

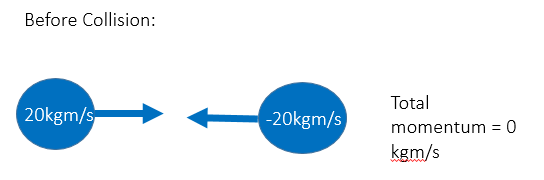
Conservation of Momentum

The principle of conservation of momentum is that the total momentum of s group of objects before a collision is equal to the total momentum after the collision.

Example 1 – two objects that join together after colliding:

Motion, figure 1

Motion, figure 2

Example 2 – two objects collide and bounce off each other:

Motion, figure 3

Motion, figure 4

(NB a total momentum of zero between the two objects does not mean they are not moving, but that they are moving with equal momentum in opposite directions.)

Worked Example 1

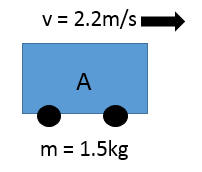
Trolley A has a mass of 1.5kg and is pushed into trolley B at a velocity of 2.2m/s. Trolley B has a mass of 0.5kg and is not moving. After the impact the trolleys stick together

Calculate:

  1. The momentum of trolley A before the impact
  2. The velocity of the two trolleys after the impact

Motion, figure 5

1

Motion, figure 6

Momentum = mass x velocity

Momentum = 1.5 x 2.2

Momentum = 3.3 kgm/s

2

Motion, figure 7

Momentum before collision = 3.3 kgm/s

Therefore, Momentum after collision = 3.3 kgm/s (no calculation necessary, just use the principle of the conservation of momentum)

Velocity = momentum ÷ mass

Velocity = 3.3 ÷ 2

Velocity = 1.65 m/s

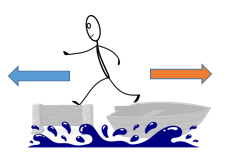
Worked Example 2

A man of mass 80kg jumps from a boat of mass 8000kg to the pier at a speed of 4m/s. Describe the motion of the boat.

Motion, figure 8

  1. Total momentum before jump = 0 kgm/s
  2. Total momentum after jump = 0 kgm/s
  3. Man: momentum after jump = 320 kgm/s
  4. Boat: momentum after jump = -320 kgm/s
  5. Boat: velocity = -0.04m/s

Changes in Momentum

To change the momentum of an object, a force is required. The relationship between force, change in momentum and the time taken for the momentum to change is shown by this equation (you do NOT need to remember this equation for the exam):

F = Δp ÷ t

F = force (N)

Δp = momentum (kgm/s)

__t __= time (s)

In a car crash, there is a sudden change in momentum, which means there is a large force on the passengers. Increasing the time taken for the change in momentum will reduce the force on the passengers, therefore reducing the chance of injury.

Crumple Zone

Motion, figure 1

The front of car is designed to crumple more easily than the rest, this is known as a crumple zone. The crumple zone means that the time taken to stop (in a crash) is slightly increased (change of momentum takes longer). This increase in time means that there is less force applied to the passenger and so there is less chance of injury.

Video - Physics of crumple zones

Video - Crumple zones and momentum

Seatbelt

Motion, figure 2

A seatbelt applies a force to slow you down in a collision as your body will continue moving forwards until a force is applied. It is made from a material that is strong enough to stop you before you hit steering wheel but that is also slightly flexible to increase time taken for change in momentum, reducing the chance of injury. It also spreads the force over a wider area of the body, reducing the pressure on any one particular part.

Video – Seat belt testing

Airbag

Motion, figure 3

An airbag inflates in a collision to apply force to slow you down, before you hit the (harder) steering wheel or dashboard. It is made from a more flexible material than steering wheel which increases the time taken for change in momentum. This reduces the force on the passenger. The force is also spread out over a greater area of the body, reducing the pressure on any one particular part.

Video - Air bag

Crash Helmet

Motion, figure 4

A crash helmet is made from a more flexible material than your skull! This increases the time taken for the change in momentum, reducing the risk of injury. Some of the energy of the collision is dissipated in cracking the outer shell of the helmet, meaning less is transferred to your skull.

Video - Crash helmet

A man travels 10m in 5s. What is his speed?
Your answer should include: 2m/s / 2
Explanation: 2m/s
How long will it take for a plane to travel 1m if it's speed is 100m/s?
Your answer should include: 1ms / 1
Explanation: 1ms
Calculate the acceleration of a car if increases its velocity from 0m/s to 15m/s in 3s.
5
Calculate the momentum of an 80kg man running at 5m/s.
Your answer should include: 400kgm/s / 400
Explanation: 400kgm/s
If a car accelerates at 5m/s2 from rest for 4s, what is its velocity?
Your answer should include: 20m/s / 20
Explanation: 20m/s