Injections and Withdrawals

In the simple model of the circular flow we looked at in 2.4.1, the level of national income was in stable equilibrium; all income received by households was spent on the goods and services produced by firms.

In the real world, the circular flow is more complex; there are additional kinds of spending that are not from households. These are called __injections (J) __into the circular flow.

There are 3 Injections

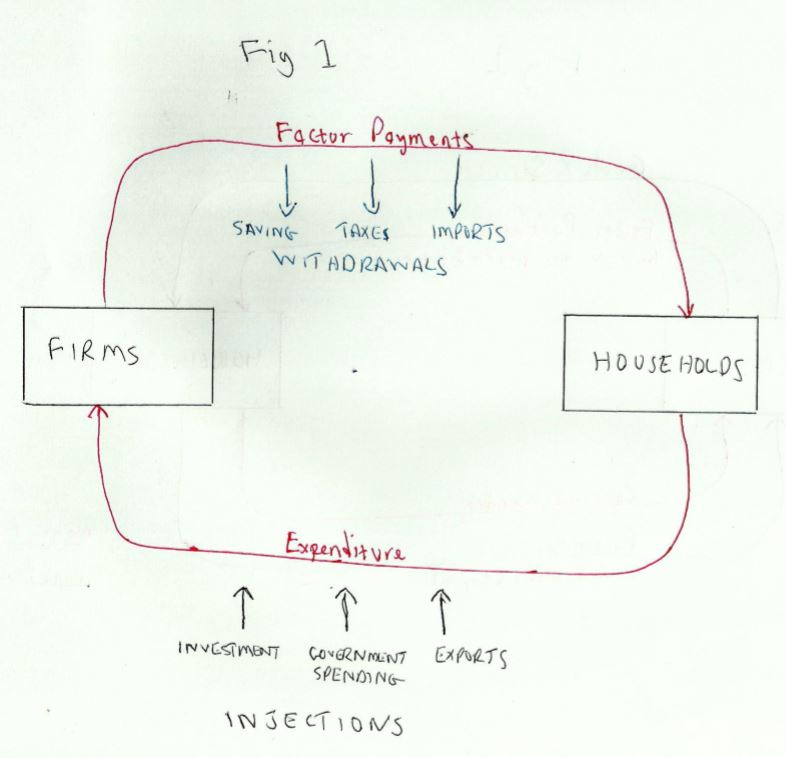
Investment (I) – Spending by firms on machines, buildings and stocks of materials and components
Government spending (G) – Spending on public services, undertaken by central government and local authorities
Exports (X) – Spending by other countries on goods and services produced in the domestic economy

There are also __withdrawals (W) __or __leakages __from the circular flow. These are income that is not spent on domestically produced goods and services.

Again, There are 3 Withdrawals

Saving (S) – households usually save some of their income rather than spend it. Firms may also retain some of their profits so that they can finance some of their investment.
Taxes (T) – are paid by households and firms; this also reduces the amount of income that can be spent.
Imports (M) – spending on goods and services produced abroad is not passed on in the domestic economy.

A revised model showing J and W is shown in _Fig 1 _below:

Equilibrium

In an economy where there are injections and withdrawals, the level of national income (Y) will be in equilibrium (no tendency to rise or fall) provided that:

Total Injections (I + G + X) = Total Withdrawals (S + T + M)

If injections are greater than withdrawals, Y will increase. As Y increases, S, T & M will also increase, as households will save more, pay more tax and buy more goods from abroad. Y will continue to rise until injections and withdrawals are equal.

If withdrawals are greater than injections, Y will fall. As Y falls, withdrawals will fall until injections and withdrawals are equal.