Expanding and Factorising
Expanding more than one bracket
Double brackets
When it comes to multiplying double brackets there are lots of different methods. There is the FOIL method- first, outside, inside, last, or there is the method that I would recommend below:
Expand and simplify:
(3a + 4) (2a - 3)
When it comes to double brackets you need to make sure you have multiplied each term in each bracket by each other, therefore:
Step 1: Rewrite the expression so you can see that each term in the first bracket will need to be multiplied by each term in the second bracket.
=(3a + 4) (2a - 3)
=3a (2a - 3) + 4(2a - 3) Now you can expand the brackets like we did for each single bracket:
Step 2: Expand the brackets as if they are two single brackets.
=3a (2a - 3) + 4(2a - 3)
=3a x 2a +3a x -3 + 4 x 2a + 4x - 3
=6a2 - 9a + 8a -12
Step 3: Colour code or differentiate the like terms and collect them together.
=6a2 - 9a + 8a - 12
=6a2 - 9a + 8a - 12
=6a2 - a - 12
Triple brackets
Sometimes you may be asked to expand more than two brackets such as (x + 4) (x + 3) (x + 5) or (x + 5)3 or (x - 6) (x + 5)2. When it comes to triple brackets just break it down. Expand two bracket and then multiply your answer by the third bracket. Eg. (x + 4) (x + 3) (x + 5). Let’s start with (x + 4) (x + 3).
Following the method above when we expand these brackets we get: x2 + 7x + 12 now we have to multiply this answer by everything that is in the remaining bracket: (x2 + 7x + 12) (x + 5). As before I would recommend writing this out as separate single brackets:
Eg. (x2 + 7x + 12)
=x2 (x + 5) + 7x(x + 5) + 12( x + 5)
Expand the brackets and then simplify your answer by collecting the like terms.
=x3 + 5 x 2 + 7 x 2 + 35x + 12x + 60
=x3 + 12 x 2 + 47x + 60
Make sure you double check your answer!
Factorising quadratic expresssions
We also need to know how to factorise more difficult expressions and equations such as x2 + x - 6 with quadratic equations we will need to put them into two brackets. Here’s how:
Step 1: Find the factors of -6 (remember - x + = -)
1 x -6 or -1 x 6
2 x -3 or -2 x 3
Step 2: Look for the factors that add together to make 1 (this will later mean they make 1x or x)
1 x -6 or -1 x 6
2 x -3 or -2 x 3 These factors add to make 1, -2 + 3 = 1
Step 3: Rewrite the quadratic equation. Change the x into -2x + 3x = x
=x2 + x - 6
=x2 - 2x + 3x - 6
Step 4: Separate the terms to make two expressions to factorise:
=x2 - 2x + 3x - 6
=x2 - 2x + 3x - 6 (make sure its +3x)
Step 5: Factorise each expression
=x2 - 2x + 3x - 6
=x(x - 2) + 3(x - 2) The contents of both the brackets should be the same!
Step 6: Put the terms outside the bracket in one bracket, and the same bracket next to it.
=x(x - 2) + 3(x - 2)
=(x + 3) (x - 2)
Step 7: Check your answer by expanding both brackets
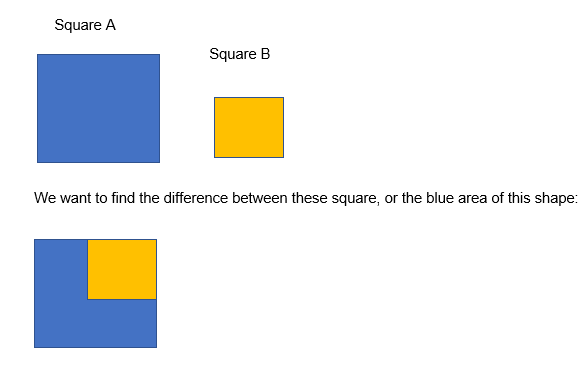
The difference of two squares
The difference of two squares describes the difference in the area of two squares. For example:
Algebraically this looks like: A2 - B2. However, we can factorise this to make it into the format (A - B) (A + B).
If you see two brackets in a format (x + a) (x - a) such as (x + 2) (x - 2) straight away you will be able to expand the brackets to make xc - a2 or x2 - 4.
Competing the square
Completing the square of a quadratic means that you need to write it in a different format. We want to change a x 2 + bx + c into a format where (x + p)2 + q. To do this follow the steps below:
Step 1: Label your numbers.
ax2 + bx + c firstly label the numbers in your expression a, b and c
Eg. x2 + 2x + 6 a=1, b=2, c=6
In cases where you have ax (eg. 2 x 2 + 4x + 12 divide every term by a)
Step 2: Write out the formula.
(x + b/2)2 + q Eg. (x + 2/2)2 + 6
(x + 1)2 + 6
Step 3: Expand the bracket and compare your new equation with your old equation
(x + 1)2 + 6 = x2 + 2x + 7
This is one more than our original equation. Therefore we need to subtract 1 from the original equation. This means we only need to add on 5, rather than 6 as we did before.
(x + 1)2 + 1 = compare this to the original x2 + 2x + 1
x2 + 2x + 6 therefore you need to add on 5
=(x + 1)2 + 5
- Expand and simplify (x + 1) (x - 4) (x + 2)
- x^3 - x^2 - 10x - 8
- Factorise x^2 - 2x - 8
- (x - 4) (x + 2)
- Using completing the square, factorise: x^2 + 6x + 7
- (x + 3)^2 - 2
Completing the square
Completing the square of a quadratic means that you need to write it in a different format. We want to change a x 2 + bx + c into a format where (x + p)2 + q. To do this follow the steps below:
Step 1: Label your numbers.
ax2 + bx + c firstly label the numbers in your expression a, b and c
Eg. x2 + 2x + 6 a=1, b=2, c=6
In cases where you have ax (eg. 2 x 2 + 4x + 12 divide every term by a)
Step 2: Write out the formula.
(x + b/2)2 + q Eg. (x + 2/2)2 + 6
(x + 1)2 + 6
Step 3: Expand the bracket and compare your new equation with your old equation
(x + 1)2 + 6 = x2 + 2x + 7
This is one more than our original equation. Therefore we need to subtract 1 from the original equation. This means we only need to add on 5, rather than 6 as we did before.
(x + 1)2 + 1 = compare this to the original x2 + 2x + 1
x2 + 2x + 6 therefore you need to add on 5
=(x + 1)2 + 5