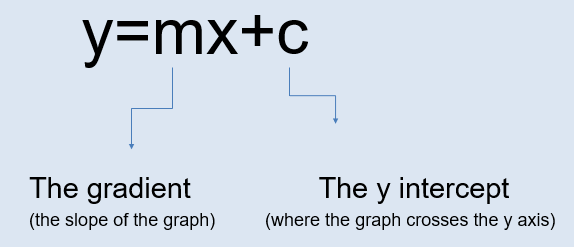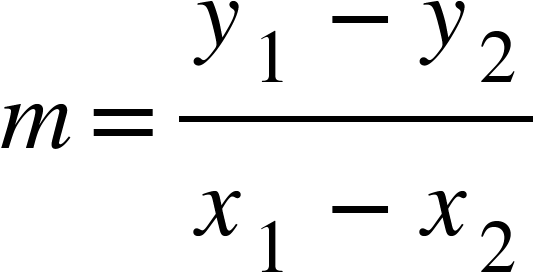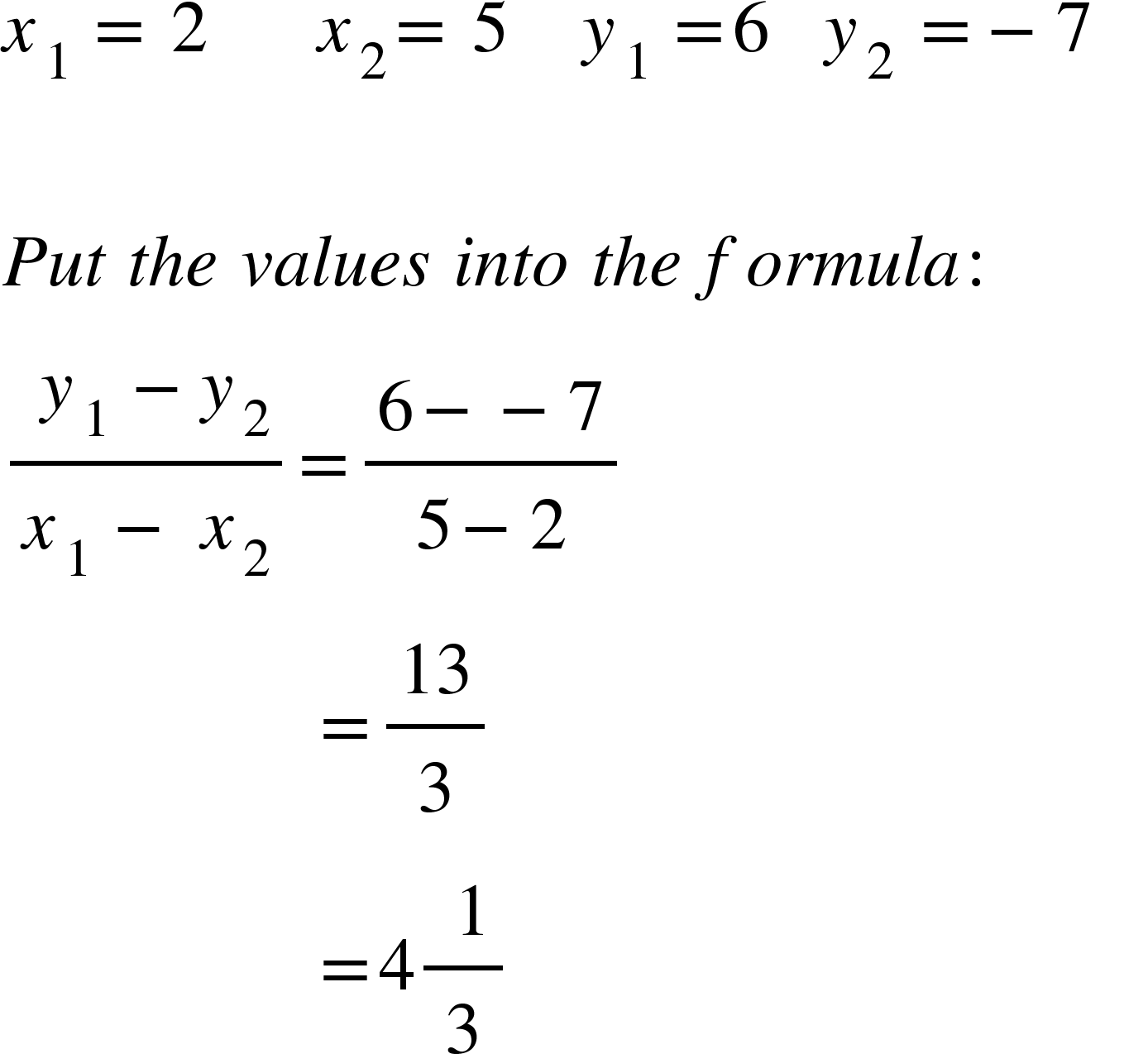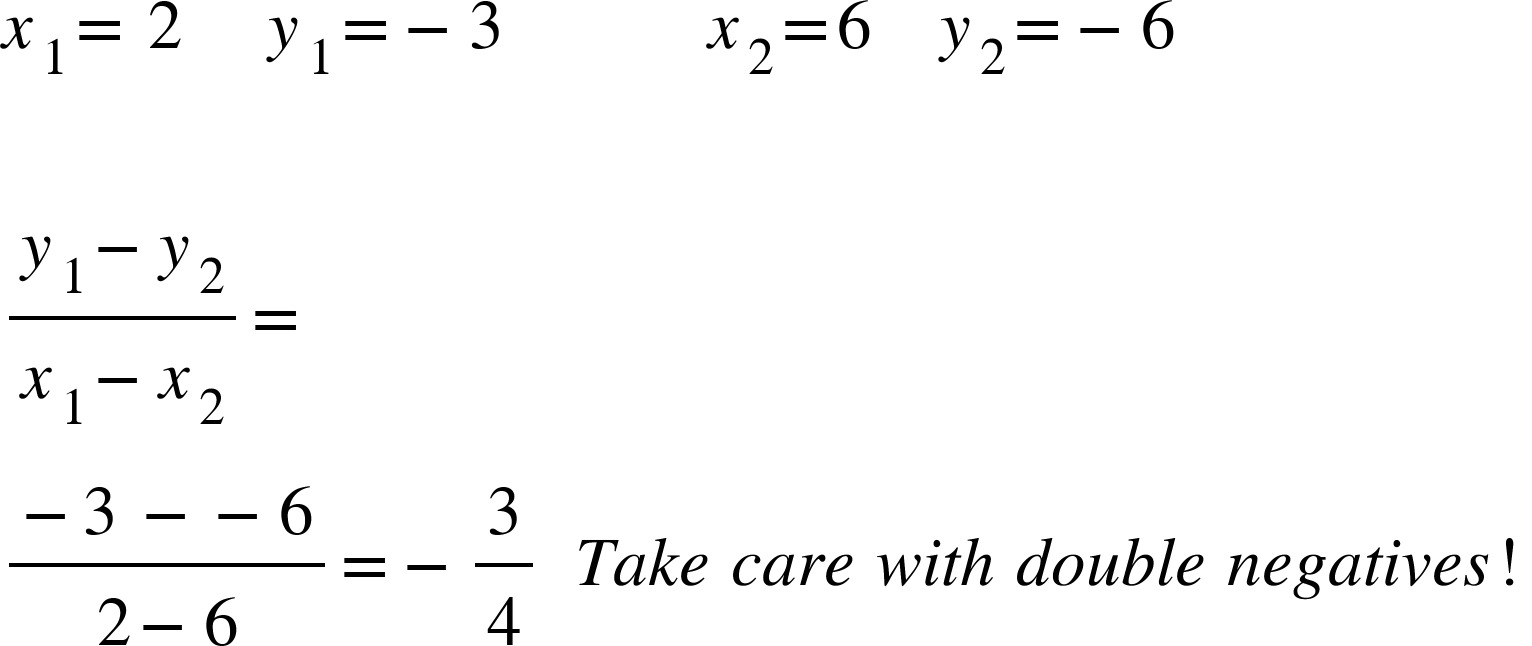Finding the Equation of a Line

Parallel lines

When it comes to drawing and identifying graphs it is important to remember the equation of a line.

In this format we can easily identify the gradient and the y intercept of the line.

Parallel lines never cross… just like train tracks!

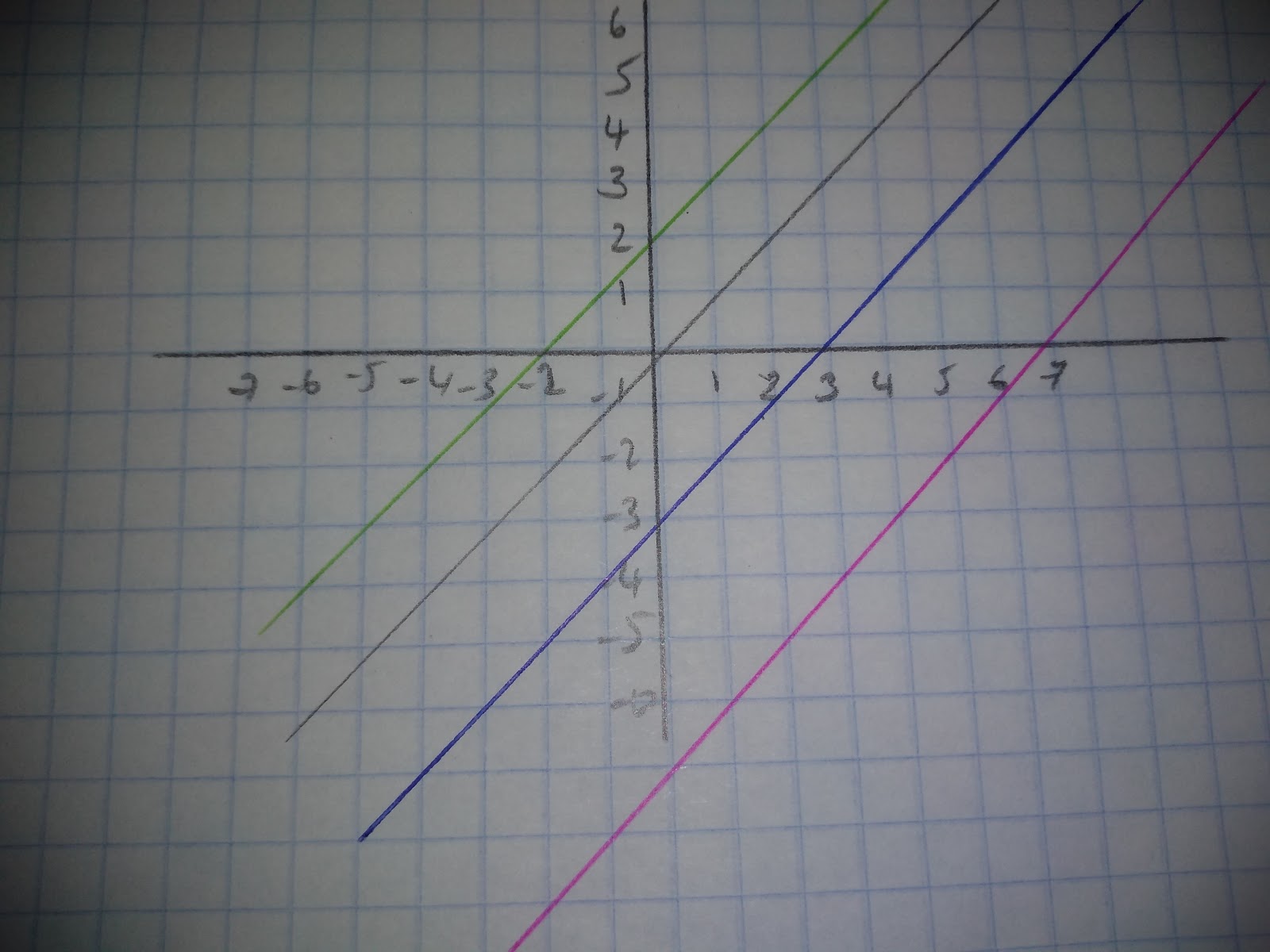
Lines that are parallel always have the same gradient. As you can see below, they cross the y axis in different places (the ‘c’ part of the equation) however the ‘m’ will always be the same for parallel lines.

Perpendicular lines

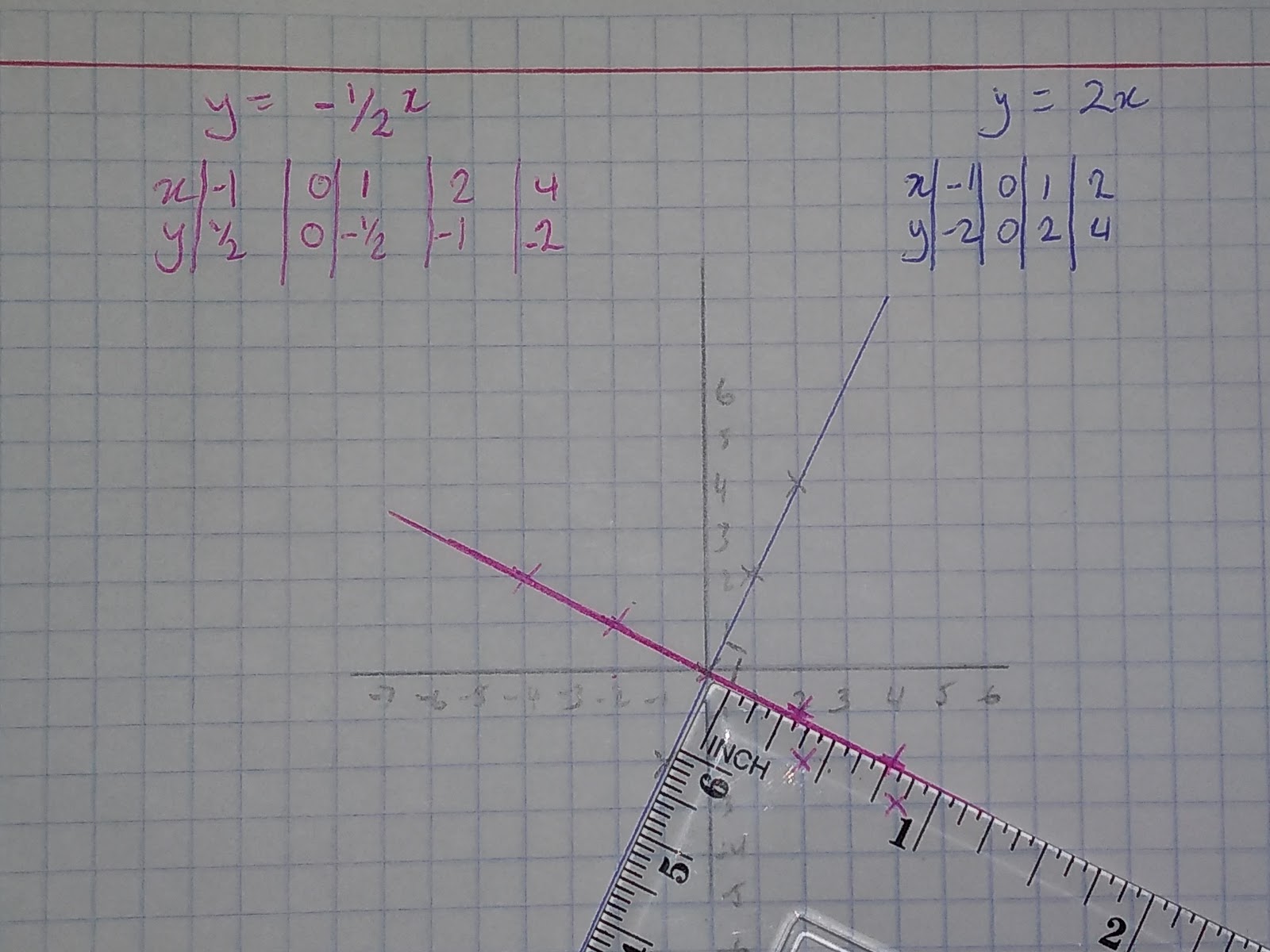
If lines are perpendicular, the gradient of one line will be the negative reciprocal. This means to find a perpendicular line multiply the gradient of the original line by -1 of the reciprocal.

For example, if the gradient of a graph is y = 2x the gradient = 2

Therefore 2 x -1 = -2 the reciprocal of -2 = -½ so, the gradient of the perpendicular line = -½

As you can see from the set square, the two lines meet a right angle.

Finding the gradient of a line

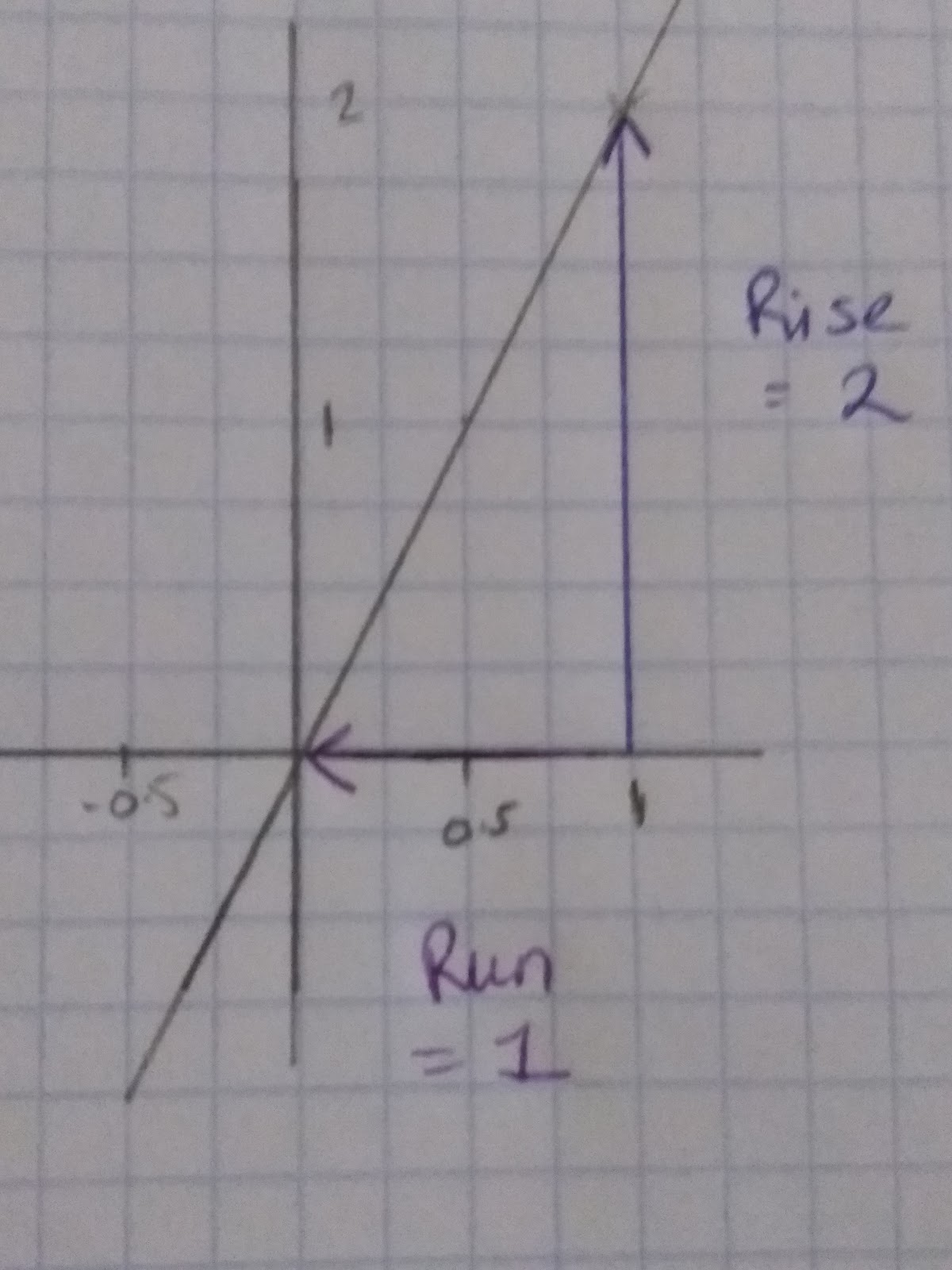
The gradient of a line is a point on the slope of the line. Here’s how you can find the gradient visually.

The gradient = Rise/Run

Example 1: The gradient = 2/1 = 2

The gradient is positive, we can check this because it is going from bottom left to top right.

Example 2: Before we even work out the gradient of the graph to the right we can see that it will be negative. This is because it goes from top left sloping downwards to bottom left.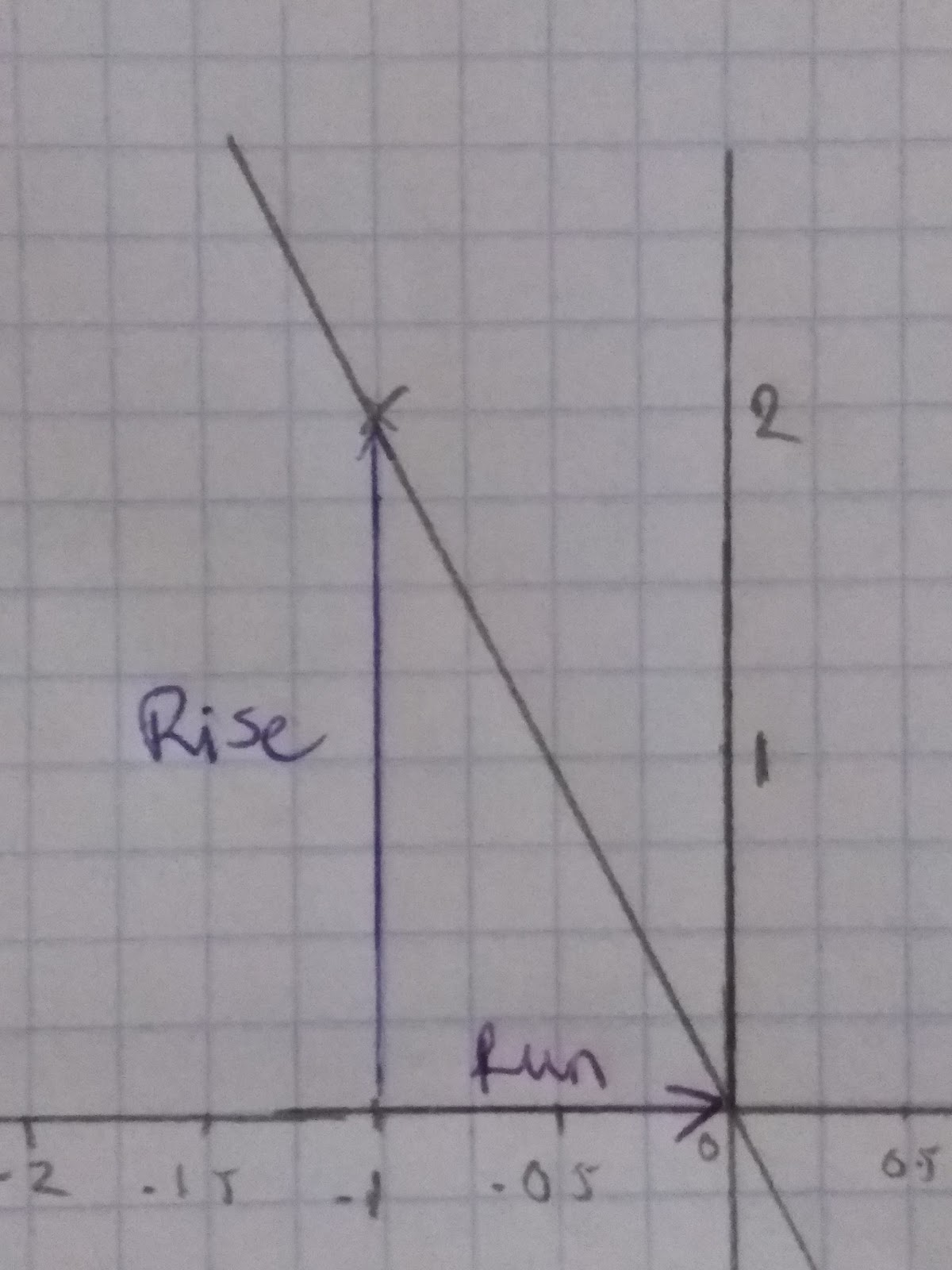

We work out the gradient as we did before:

Gradient= Rise/Run

Gradient = 2/-1 = -2

The Gradient can also be written as a formula: Gradient = Difference in y coordinates/Difference in x coordinates

Or, if we label two coordinates on the graph, one A and one B, we could say:

A: (x1 , y1) B: (x2 , y2)

We can then substitute our values into this formula to work out the gradient:

Using this formula we can work out the gradient between two given points. Eg. What is the gradient between (2, 6) and (5, -7).

Label the coordinates

The equation of a line through one point and a gradient

Remember, the equation of a line is y=mx+c and to find the equation of a line all we need is one point (x, y) and the gradient ‘m’ of the line. For example, if I know that a line has a gradient of 4 and passes through the point (2, 3) we can work out the equation of the line.

Firstly we need to think about the information that I have and the information we need. So, we know that when x=2, y=3, and the m=4. If we put this information into the equation of a line it’ll look like this:

y=mx+c

y=4x+c

Using the points we can create an equation to work out the ‘c’ of the equation:

3=4(2)+c

3=8+c

-5=c

Now we know ‘c’ we have the equation of the line:

y=4x -5

The equation of a line with two points

Given that all we need to work out the gradient is two points and that we only need one point plus the gradient to find the equation of a line, we can work out the equation of a line using only two points. For example, what is the line that passes through the points (2, -3) and (6, -6).

So thinking of the equation y=mx+c first we need to find the gradient. As before we can use the formula:

Now that we know our gradient is -¾ we can start forming our equation.

y=-¾ x +c

We can use either point to work out c

-3 = -¾ (2) + c

-3 = -1.5 + c

-1.5 = c

y = -¾ x -1.5 We can use our second point to check that we are correct.

-6 = -¾ (6) -4.5

-6 = -1.5 - 4.5

= -6

The y value is equal to -6, therefore we know that we are correct.

Which lines are perpendicular to y= 7x +3? a) y=7x +1 b) y=-1x +6, c)7y = 6 - x

Your answer should include: b / c

Find the gradient between the points (4,6) and (-2, -5) give you answer to 2 dp.

1.83