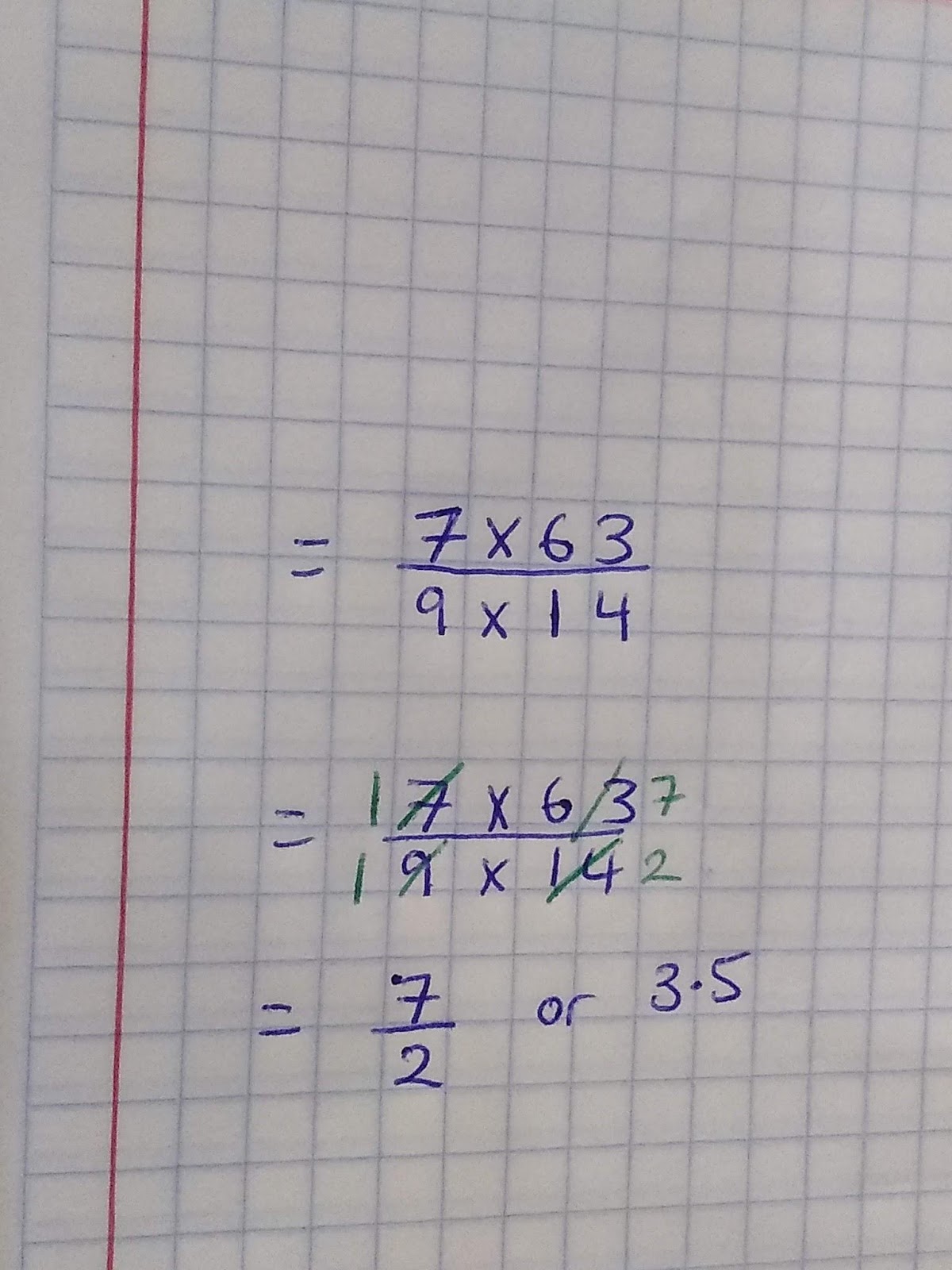Calculations

Bidmas or Bodmas

Brackets ()

Indices / Powers Of

Division /

Multiplication x

Addition +

Subtraction -

BIDMAS or BODMAS stands for the order of operations. Just as grammar helps us understand sentences, the acronyms BIDMAS or BODMAS or PODMAS (brackets=parenthesis in the USA), makes sure we’re all calculating in the same way. The key is to complete each process in a calculation before moving onto the next one. When it comes to addition and subtraction though just work left to right.

Eg. 4 + 5 x 7 - 32 + (4 x 2)

= 4 + 5 x 7 + 32 - 8 Complete one step at a time, and show your working out!

= 4 + 5 x 7 +9 - 8

= 4 + 35 +9 - 8 Remember it’s always left to right with addition and subtraction.

= 40

These rules are very important and also apply when you are manipulating algebraic equations or expressions too!

__Top tip: __Make an effort with your working out, keep it neat and line up the equal signs. This will help you show your working to the examiner and it will also enable you to check that you’ve gone through BIDMAS for each line of your working.

Inverse Operations

Basics:

Being able to unravel an equation relies on us understanding inverse operations.

Here’s a quick recap of the basic inverse operations:

The opposite of adding is subtraction.

The opposite of multiplying is dividing.

The opposite of a power is a root.

These rules are very important, especially when we want to simplify calculations or expression.

Simplifying Calculations

For example, when we know multiplication and division are inverse operations it enables us to cancel down fractions such as these:

Because division and multiplication are inverse operations we can simplify across, by dividing the 14 by 7 and the 63.

Brackets

Remember that brackets require you to multiply and therefore to get rid of brackets you will need to divide.

Eg. 5(3 + x) = 10

To solve the equation, the first thing you need to do is divide both sides by 5, therefore:

5(3 + x) = 10

3 + x =5

x=2

Reciprocal of a Fraction

The reciprocal of a fraction is the fraction flipped or turned upside-down. In more mathematical words, it is 1 divided by a the fraction.

Here’s some examples:

The reciprocal of 1/3 is 3/1 = 3

The reciprocal of 4/5 is 5/4

The reciprocal of 3 2/3 is 3/11. When finding the reciprocal of a mixed number, turn it into an improper fraction and then flip it!

Exact Calculations

When you are calculating it is important that you read the question carefully about how it is to be answered.

Sometimes the exam will specify that it wants you to answer a question to a certain amount, other times they will want you to write an exact answer.

This might be a specification for you to calculate something in terms of π. This means your answer would be a number x π, for example it could be 6π (which means 6 x π).

You may also need to calculate exactly by using fractions or surds. If it asks for an exact answer, it is always best to leave your answer as a surd or a fraction.

What is the reciprocal of 5 2/3?

3/17
Explanation: 5 2/3 is a mixed number, so you need to turn it into an improper fraction (17/3), and then flip it.