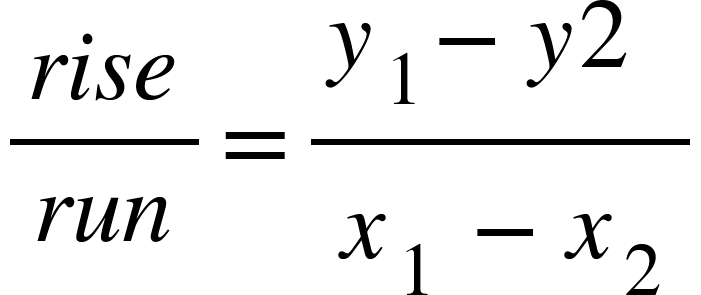Interpreting Graphs
Gradients and rates of change
When it comes to interpreting graphs we need to remember how to calculate the gradient and the equation of a line. If you need to go over this in more detail look at Calculating and Estimating Gradients of Graphs.
The key points to remember when looking at linear gradients is that the gradient can be found using the formula:
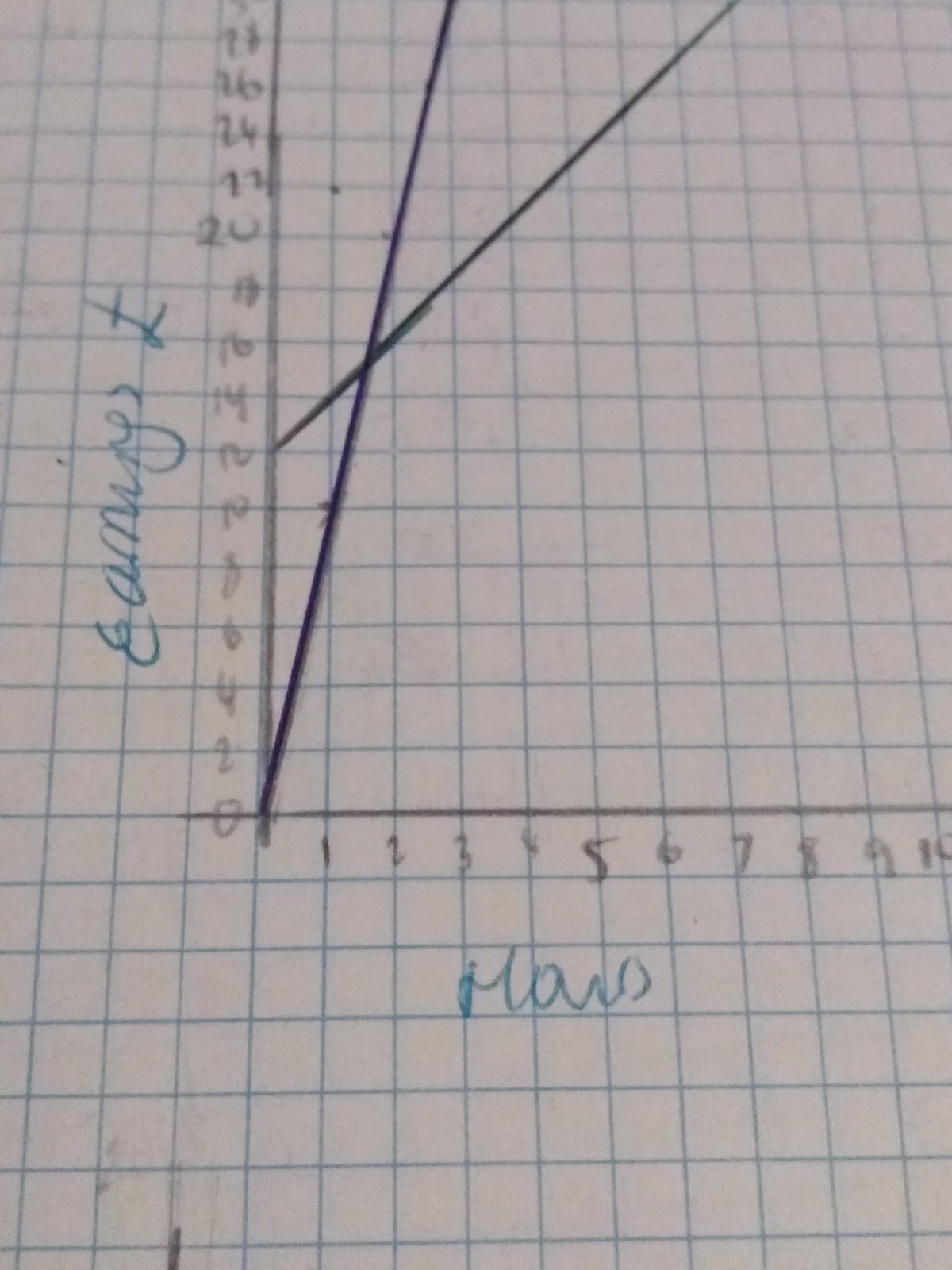
The graphs above display the rates of pay for two different builders. James (starting at 0) and Jenny (starting at 10).
James’ line shows a graph in direct proportion. We can see this because the graph increases at the same rate and starts at the origin (0,0).
Jenny’s line shows a graph that has a gentler gradient. We can tell see this when the blue line goes over it, but we can also work out the gradients of both graphs to compare them.
James’ graph has a gradient of 3 whilst Jenny’s has a gradient of 2. This tells us that per hour the Jenny earns more, however there is no starting fee, unlike the Jame’s graph. Therefore this will need to be taken into consideration when making decisions about which builder to use.
Graphs illustrating direct and inverse proportion
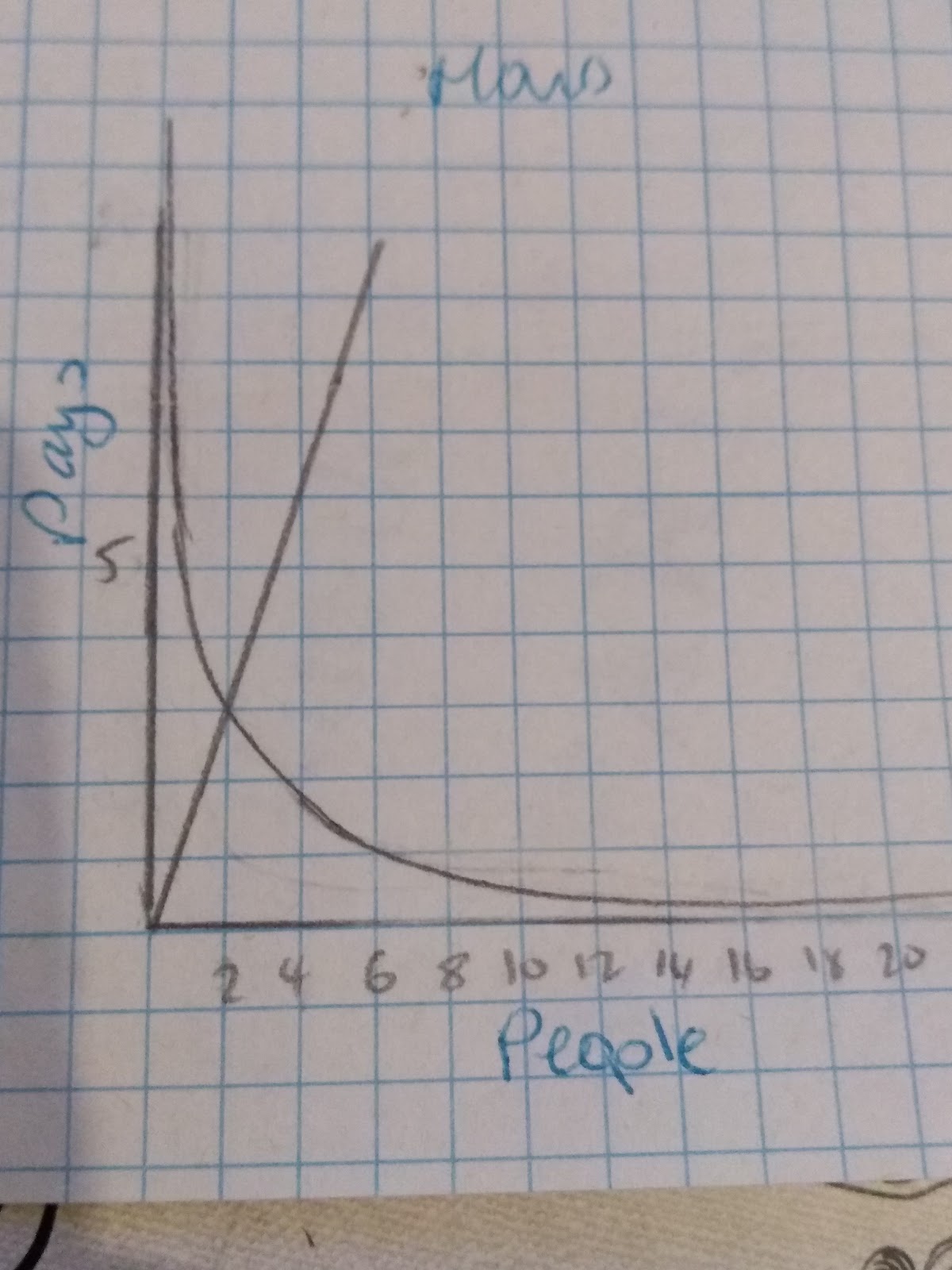
Being able to recognise graphs of direct and inverse proportion is very important.
Key aspects of direct proportion:
- The graph will go through the point ( 0,0) - the origin
- The variables will increase proportionally, this will show a straight line with a constant gradient
Key aspect of inverse proportion:
- The graph has a reciprocal shape
- As one variable increase the other variable will increase by the inverse amount. Eg. if one variable doubles the other will half.
The straight line graph is the graph showing direct proportion. The curved graph shows inverse proportion.
- What are the key features of a graph that shows direct proportion?
- Your answer should include: starts at (0 / 0) / straight line / constant gradient
- a or b? The steeper the gradient the a) Greater the rate of change? b) The more gradual the rate of change
- Your answer should include: a / a)