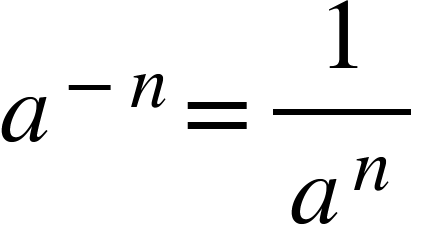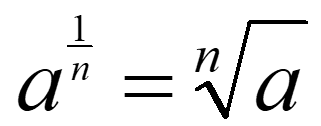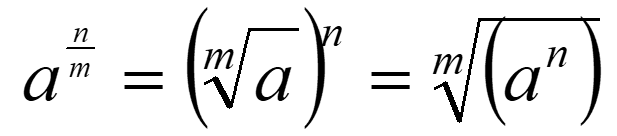Recapping Laws of Indices

Indices with algebra

As with numbers, the laws of indices also apply with algebra. Let’s recap and focus on some more difficult multiplication and division with indices.

Multiplying indices: aⁿ x a^m = a^n+m

Dividing indices aⁿ a^m = a^n-m

__Indices with brackets: __

(aⁿ)^m = (a)^{n x m}

(ab)^m = (a)^m x (b)^m

Negative indices:

__ __

Fractional Indices:

More complicated fractions:

Simplifying more complicated expressions

In the higher paper you will be expected to simplify more complicated indices that may combine indices, roots, brackets, fractions and algebra. Eg.

( The top being the numerator!)

Simplify: √16v^5t^-6 / √64vt

1/2v^2

5√c^10d^15

c^2d^3

1 / (4√m)^5

m^-5/4