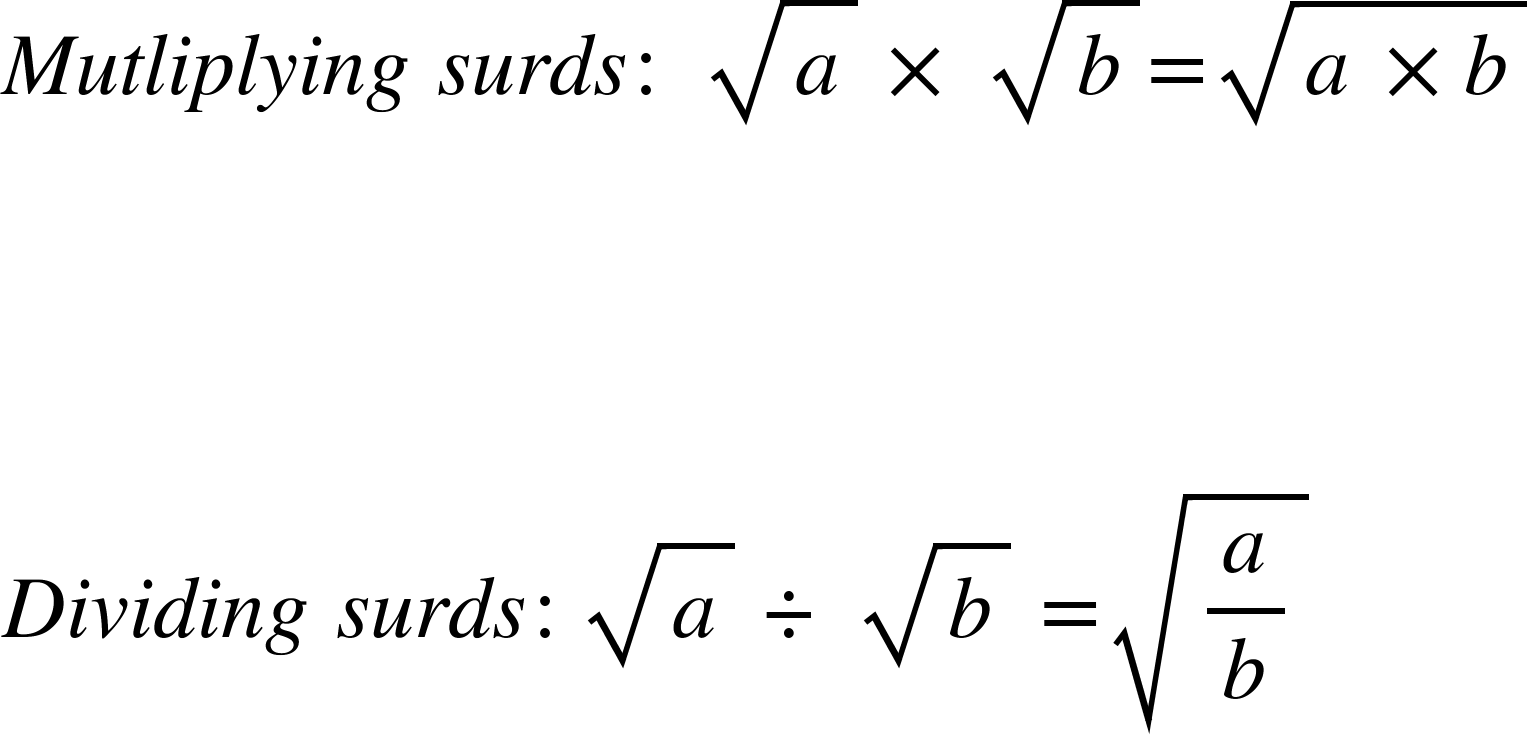Surds

Simplifying Surds

Surds, figure 1

What is a surd?

A surd is a number that is irrational. It cannot be written exactly. For example √3= 1.732051080……. It continues indefinitely and cannot be written as a fraction.

Simplifying Surds

When working with surds there are certain rules we need to learn to help us manipulate and simplify them:

Surds, figure 2Simplifying Surds:

A key thing to remember with surds is that if you can get to a square number, then you can simplify the surd!

Always aim to make square numbers under surds. This usually involves breaking a surd down into its square factors.

For example to simplify √60

Write down the factors of 60 and look for square factors

Surds, figure 3

1 x 60 , 2 x 30, 3x 20, __4 x 15, __5 x 12, 6 x 10

4 is a square number so now we have a square factor!

√60 __= __√4 x √15 __= 2√15__

15 does not have any square factors (1 x 15, 3 x 5) therefore we cannot simplify the surd anymore.

= 2√15 is our answer.

Rationalising Denominators

A key question with surds often involves rationalising a denominator.

If you remember that a surd is a square root then √ a x √ a = a

Given this sometimes you will be required to rationalise the denominator of a fraction, if it is a surd. Eg.

Surds, figure 1

By making the denominator 2 you have rationalised it!

The same logic applies for more complicated examples:

Surds, figure 2