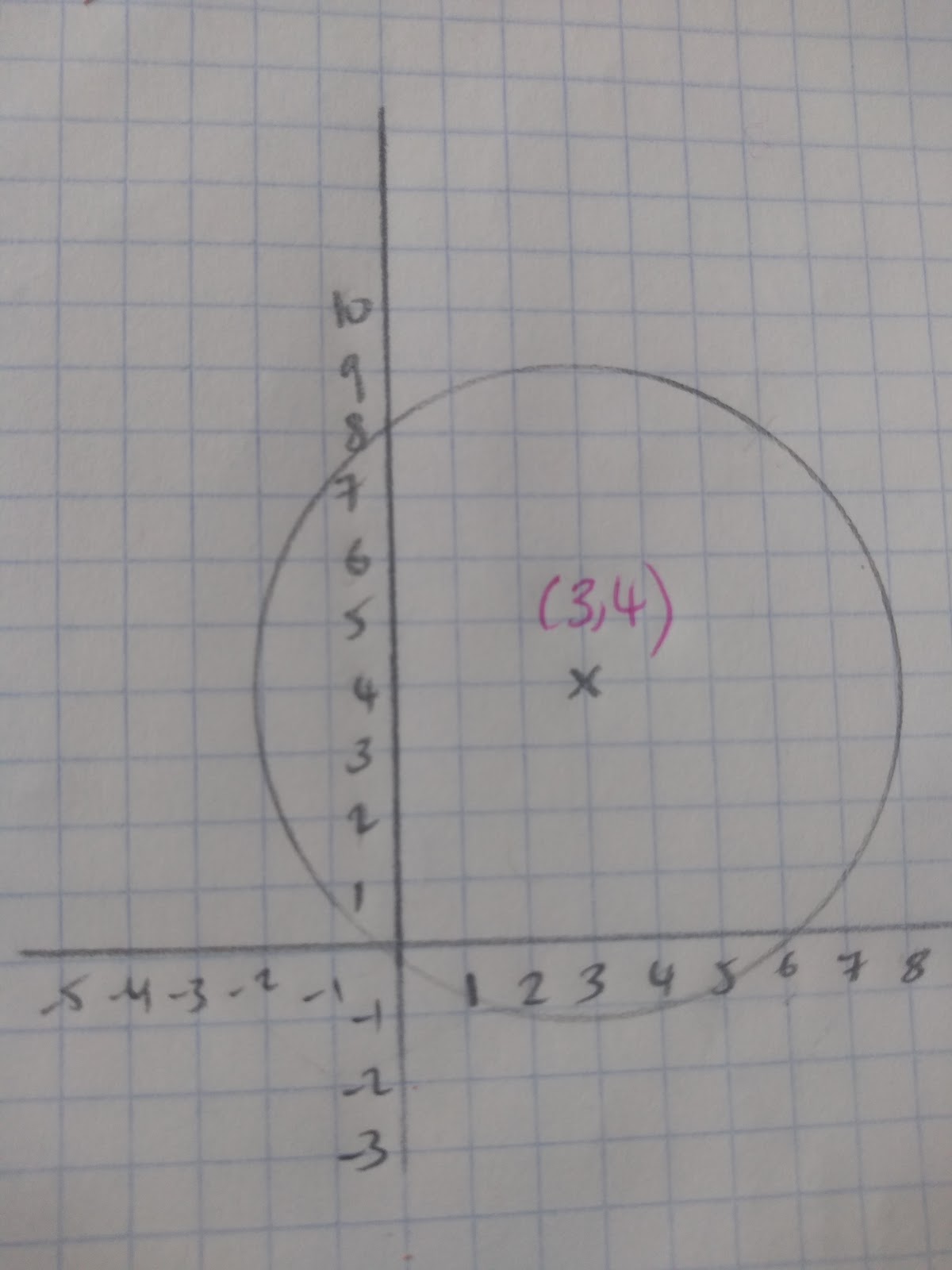The Equation of a Circle

What is the equation of a circle?

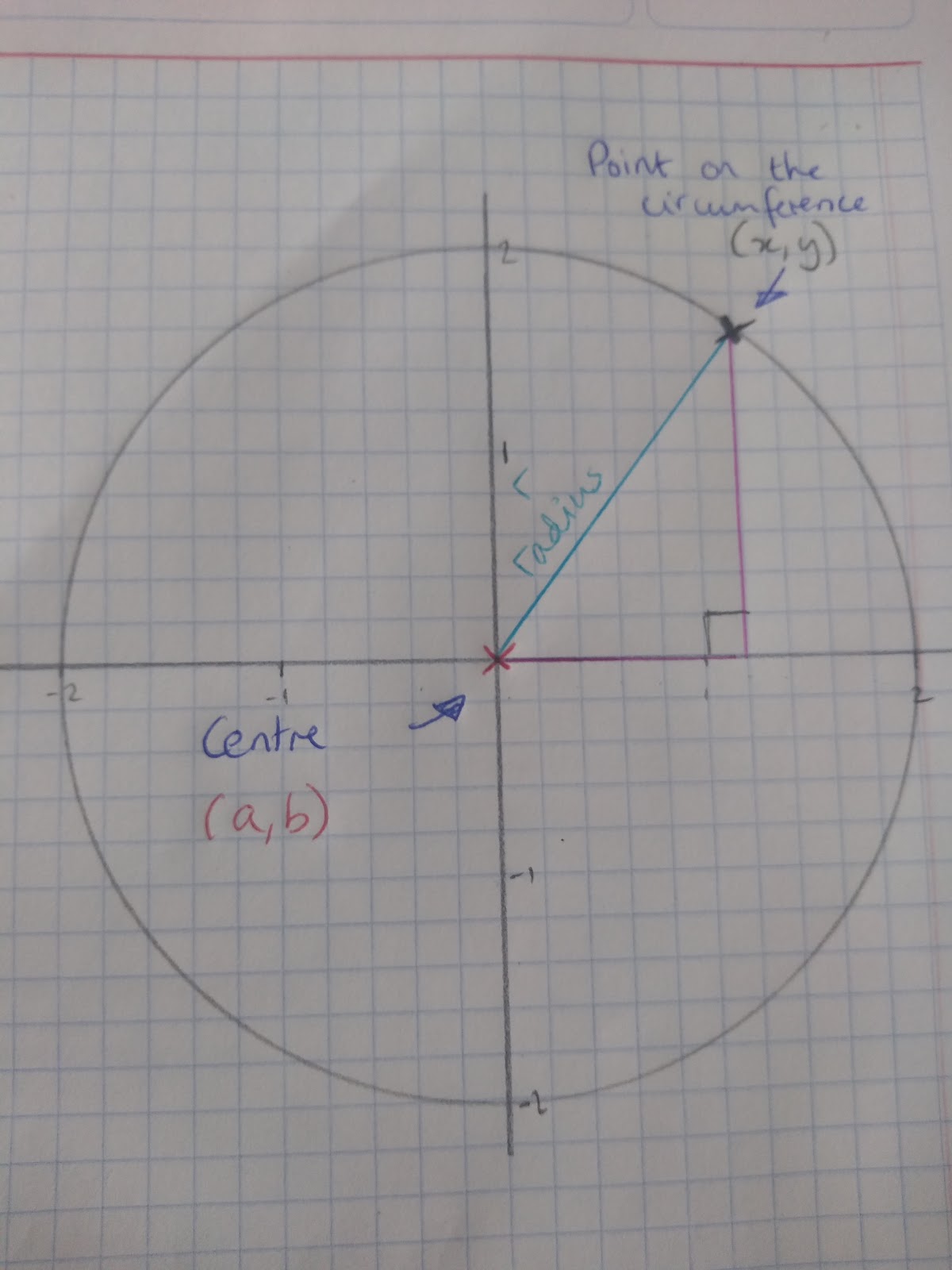
The Equation of a Circle, figure 1

The equation of a circle, where r__ = the radius (a,b) = centre of the circle and where (x,y) is a point on the circumference: __r2 =(x - a)2 + (y - b)2

This equation is derived from pythagoras’ theorem and, the key things you need to work out the equation of a circle are two of: the coordinates for the centre of the circle, the radius and a point on the outside.

Finding the Radius of a Circle

We can also use the formula to find the radius of the circle. For example, what is the radius of 36 = x2 + y2 if we know that r2 =(x -a)2 + (y - b)2 all we will need to do is to square root 36, this will give us the radius which = 6. You may have to find the equation of the circle given given the centre and one point on the circle. For example, find the equation of the circle given that the centre is (2,1) and it goes through the point (6,6).

Let’s complete our equation of a circle with what we already know:

r2 = (x -a)2 + (y - b)2

r2 = (2 -6)2 + (1 - 6)2

The key value we are missing is the radius, therefore all we need to do is substitute in our values.

r2 = (2 -6)2 + (1 - 6)2

r2 = (-4)2 + (-5)2

r2 = 16 + 25

r2 = 41

Therefore the radius = __√__41 and our equation = 412 = (x - 6)2 + (y - 6)2

Sketching a Circle

When it comes to sketching a circle, we need to remember what the elements of the formula mean. For example, sketch the circle with the equation 25 = (x-3)2 + (y- 4)2. We need to find the following to be able to sketch a circle:

  1. The radius
  2. The centre of the circle

Remembering the formula r2 = (x -a)2 + (y - b)2 to find the radius we will need to square root 25. This means the radius = 5. To find the centre of the circle we need to put a and b into coordinates: (3,4). Now we have our centre and radius we can draw our circle:

The Equation of a Circle, figure 2

Find the equation of a tangent to a circle

To find the equation of a tangent to a circle we need to remember a couple of key things:

  1. That the radius is always perpendicular to a tangent of a circle
  2. To find the gradient of a perpendicular line multiply by the negative reciprocal.
  3. Tangents are straight lines and therefore will be in the format y=mx+c

Here’s an example and the steps that you need to take:

Find the equation of the tangent to the circle 8=x2 + y2 on the point (2,2)

Step 1: Recognise the key information that you know from the equation of a circle by comparing it with the original formula:

8 = x2 + y2

r2 = (x -a)2 + (y - b)2

Radius = __√__8 Centre= (0,0) Point given= (2,2)

Step 2: Find the gradient of the radius to the point given:

Gradient between two points = 0-2/0-2

m=1

Step 3: Find the perpendicular tangent.

To do this we need to multiply by the negative reciprocal so if m=1 x 1/-1 therefore the gradient of the tangent will = -1

Step 4: Use the equation the gradient and the point to work out the equation of the tangent

y=mx+c the point (2,2)

2 = -1(2) + c

2 = -2 + c

4 = c

Therefore the equation of the tangent is y=x+4