Measures and Accuracy

Units of Measure

Writing different measures to a required level of accuracy.

Time

Measures and Accuracy, figure 1

1 second

60 seconds = 1 minute

60 minutes = 1 hour

24 hours = 1 day

30/31 days = 1 month

365 days = 1 year

Top tip: Apart from the basic facts above, it’s important to remember that time is not measured in 10s and therefore when you use decimals you need to remember that they are fractions of time. For example 1.5 days is 36 hours, the 0.5 days = 12 hours , 1 day= 24 hours.

Measures and Accuracy, figure 2

Money

When it comes to money just double check your answer. Remember £0.01 is 1 penny, check your decimal places!

Rounding Numbers

Rounding to Decimal Places

Often you will be required to round to a given number of decimal places. This is how to round.

Measures and Accuracy, figure 1

  1. Identify the number of decimal places you need to round to
  2. Look at the number ‘next door’ to the right
  3. If that number is more than five, the number that you are rounding to will go up by 1
  4. If that number is less than five keep the number as it is.

Eg. Round 0.15248 to 3 decimal places

  1. 0.15__2__48 the 2 is the third decimal place it will stay the same or increase
  2. Look next door- it’s a 4,
  3. 4 is less than 5 so we keep the 3rd decimal place as 2 and remove the 4 and the 8
  4. The final answer is 0.152

Round 0.7923 to 1 decimal place

  1. 0.__7__923 the 7 is in the 1st decimal place position
  2. Look next door it’s 9
  3. 9 is more than 5 so the 7 will change to an 8
  4. The final answer is therefore 0.8

Round 4.999 to 2 decimal places

  1. 4.9__9__9 the second 9 is in the 2nd decimal place position
  2. Look next door and it’s 9- so we will round up
  3. The 9 will change to a 10, which means it will change the second column as well!
  4. The final answer is therefore 5.00

Measures and Accuracy, figure 2

Rounding to Significant Figures

When rounding to significant figures the basic principles of rounding remain it’s just about identifying the __significant figure __that we are rounding to. To do this we need to think about the meaning that each digit in a numbers give. For example in 56,423:

5 = 50,000

6 = 6,000 (Woody’s trying to figure it out!)

4 = 400

2 = 20

3 = 3

Therefore the most significant digit that defines the number is the 5, the second most significant is the 6, the third is the 4th , the fourth significant figure is the 2 and the least significant figure in this number is the 3.

In large numbers the most significant figure is ALWAYS the number furthest to the left of the decimal point.

In very small numbers however it is slightly different.

For example: 0.0000__2__4069

2 = 0.00002

4 = 0.000004

0 = 0.0000000 - any zero after the first significant figure and in between other significant figures is counted as a significant figure.

6 = 0.00000006

9 = 0.000000009

In this number the zeros at the beginning are used as place holders. Therefore the most significant figure in this number is the 2. Once you have identified the first significant figure, you count on from there, including the remaining zeros.

Therefore 0.0000__2__4069 to:

3 significant figures = 0.0000240

4 significant figures = 0.00002407

Eg. 0.05602007

Rounded to 3 significant figures = 0.0560

In this example it is important to keep the 0 to show the level of accuracy that the number has been rounded to.

Estimating Answers

Part of the exam will require you to estimate answers. This is the process we use to estimate answers:

  1. Round the numbers to 1 significant figure
  2. Complete the calculation

Eg. (5.623 x 9.42) + 823.46 =

  1. (6 x 9) + 800 = Don’t forget BIDMAS!
  2. 54 + 800 = 854

Measures and Accuracy, figure 1

Upper and Lower Bounds

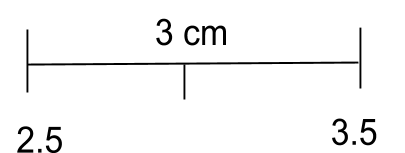
When we round, we round to an accuracy, this could be 1 decimal place, it could be to 1 cm or it could be to 0.5 of a gram. Whatever we round to there is always a limit to the accuracy of our number. For example: if a company makes matches to the nearest centimetre that means that there could be an error of + or - 0.5 cm. So if this match measured 3cm that could be a max of 3.5 cm or a minimum of 2.5 cm.

Measures and Accuracy, figure 1Measures and Accuracy, figure 2

Measures and Accuracy, figure 3

Here’s another example:

An apple weighs 70 grams to the nearest gram.

To find the bounds + or - ½ gram.

Therefore the upper bound = 70.5

And the lower bound is = 69.5

You may need to answer questions that involve finding the upper bounds with area and volume, so make sure know how to find them!

Round 0.061256 to 3 decimal places
0.061
A square has a length of 5 cm to the nearest cm. What is the largest area it could be?
30.25
Explanation: A=5.5 x 5.5 =30.25 cm squared