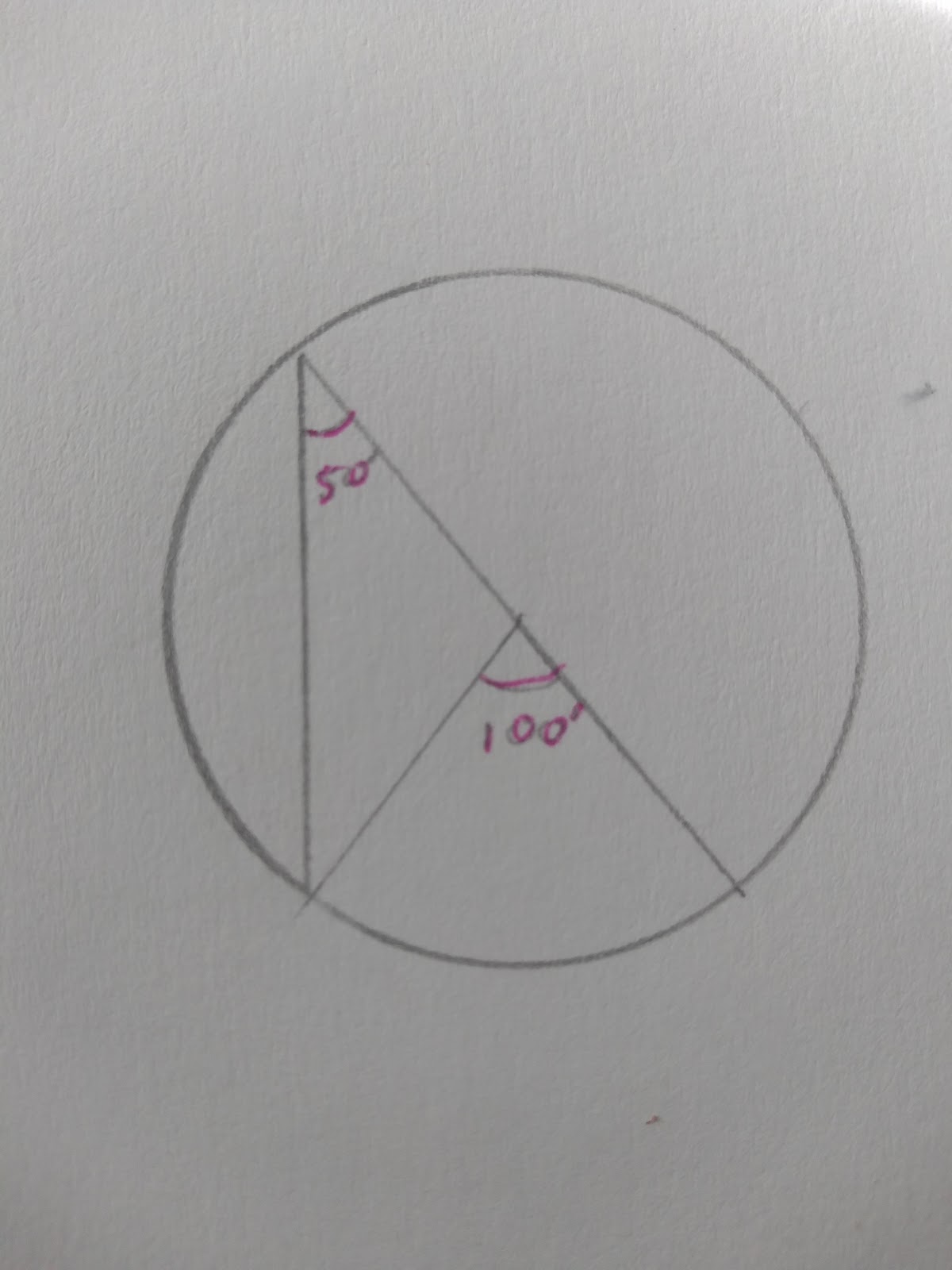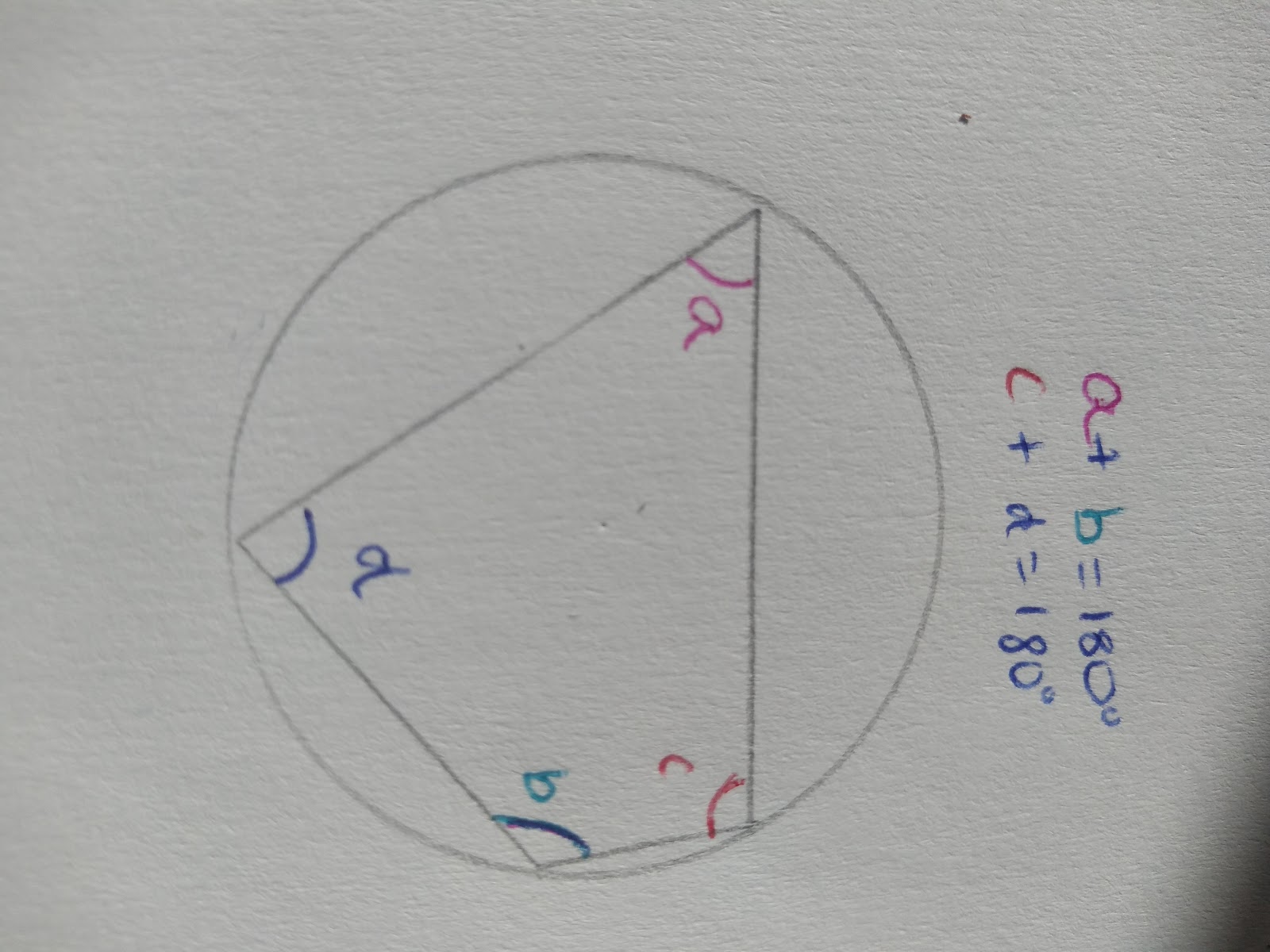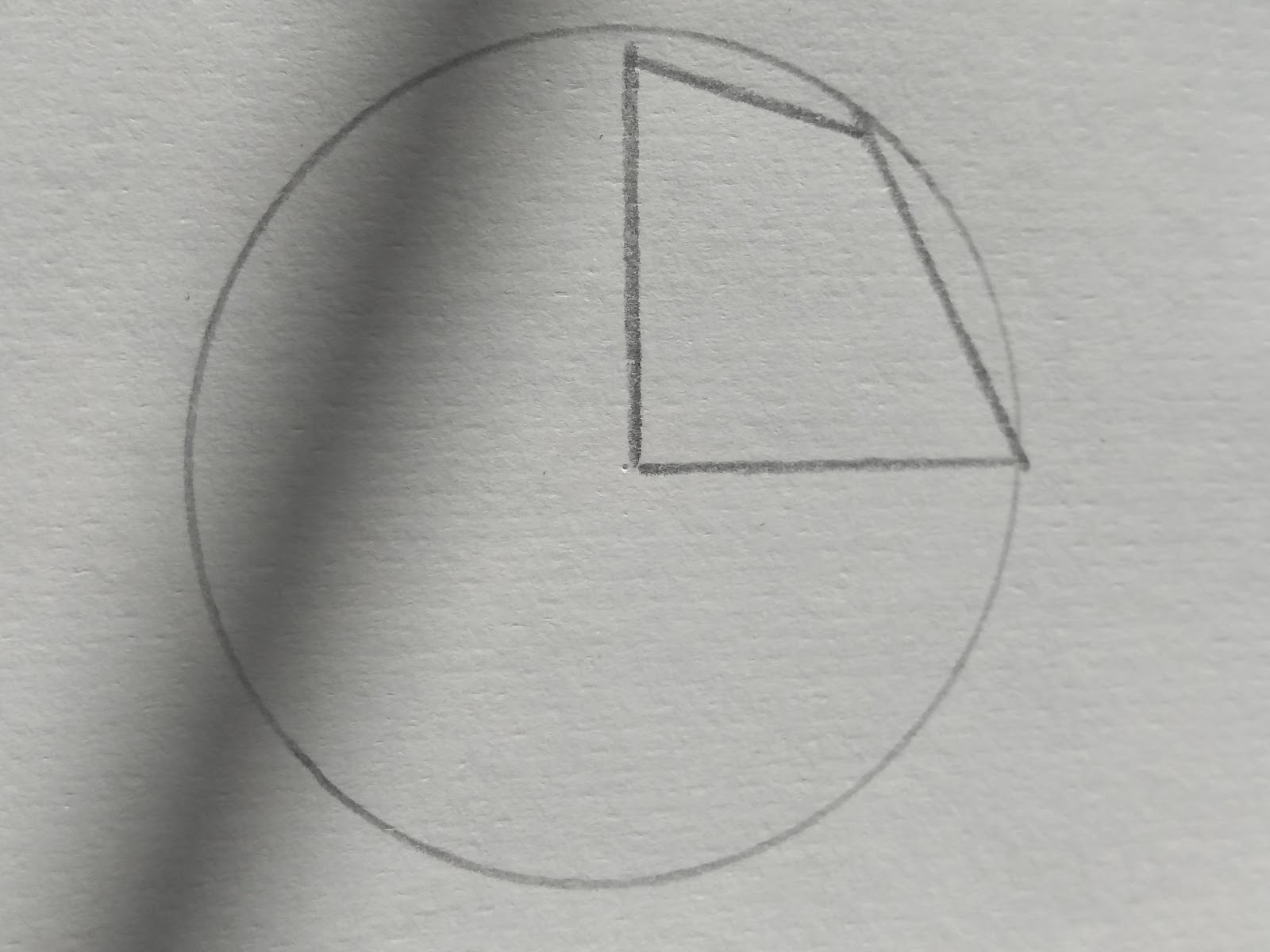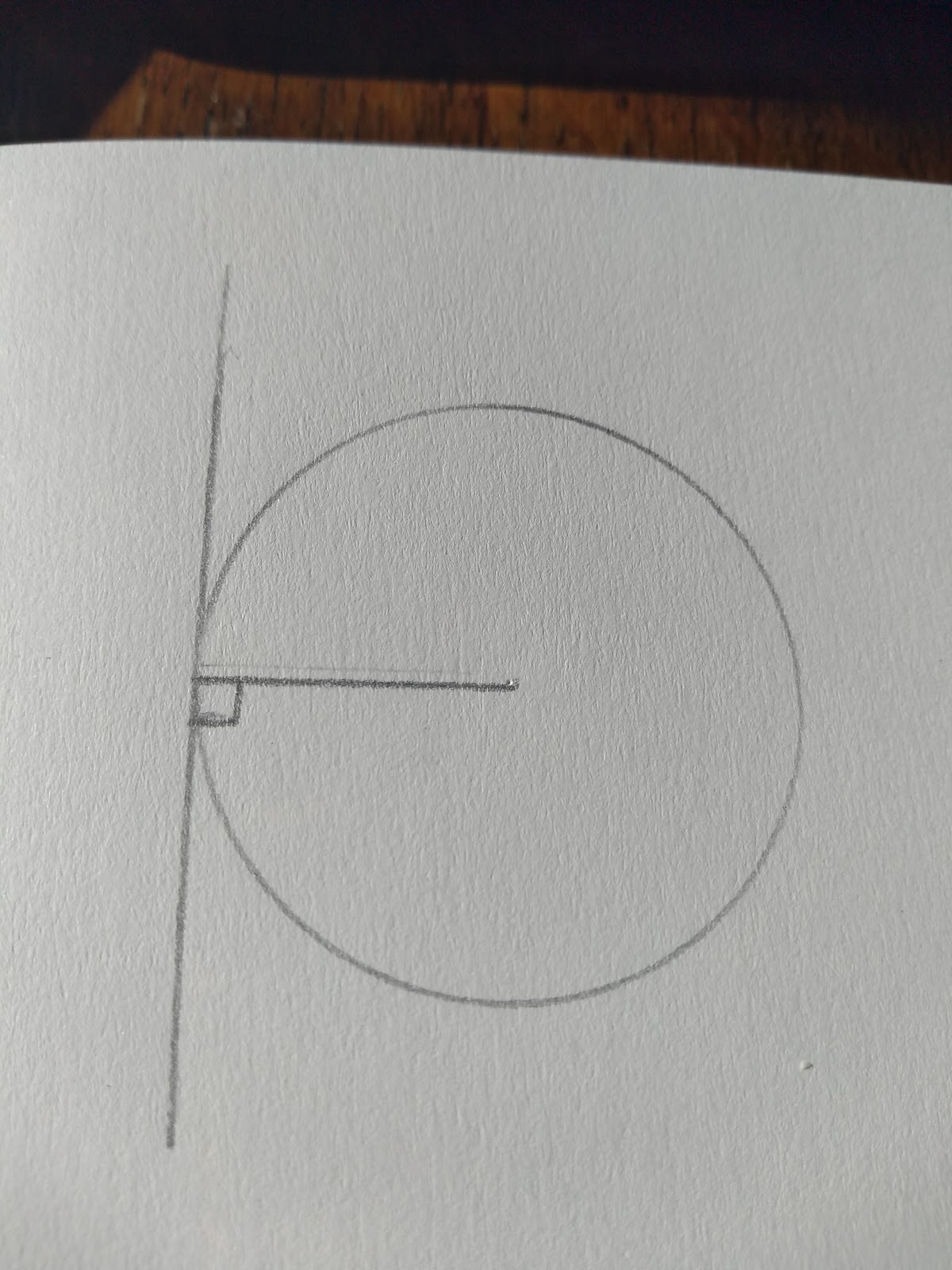Circle Theorems

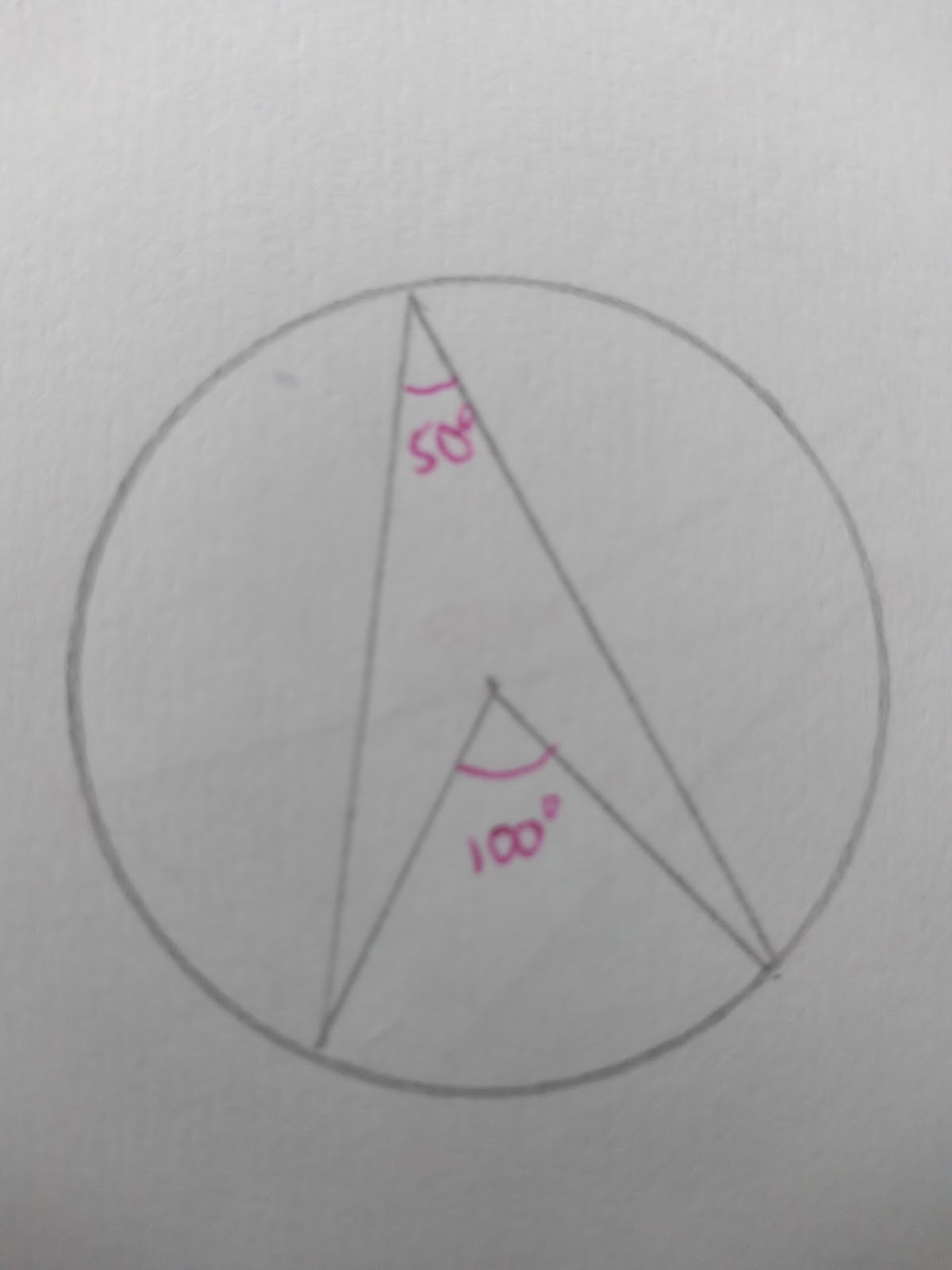
Inscribed Angle

The angle at the centre of a circle is always __double that of the angle at the circumference if both angles are ‘__subtended’ (created) from the same two points on a chord.

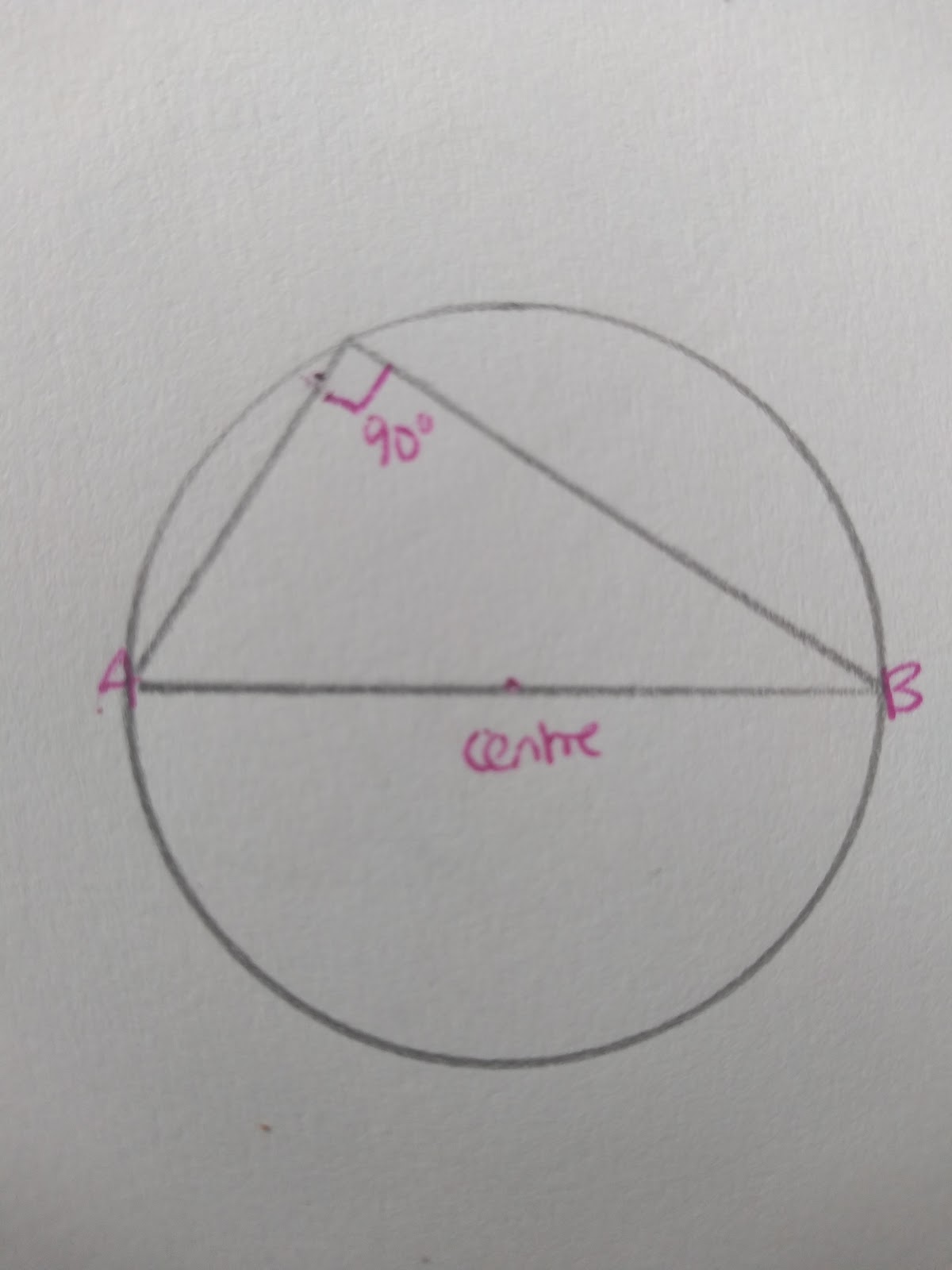
Circle Theorems, figure 1Circle Theorems, figure 2

Angles in Semicircles

Circle Theorems, figure 1

A triangle within a circle with the diameter as base will always have a right angle at the circumference.

Cyclical Quadrilaterals

Circle Theorems, figure 1

Opposite angles in a cyclic quadrilateral ( a quadrilateral in a circle) will always add to 180 degrees.

To be a cyclic quadrilateral all points of the quadrilateral must touch the circumference.

Circle Theorems, figure 2

This is not a cyclic quadrilateral as the points don’t all touch the circumference of the circle.

Tangent Angles

Circle Theorems, figure 1

Where a tangent meets a radius it creates an angles of 90 degrees.

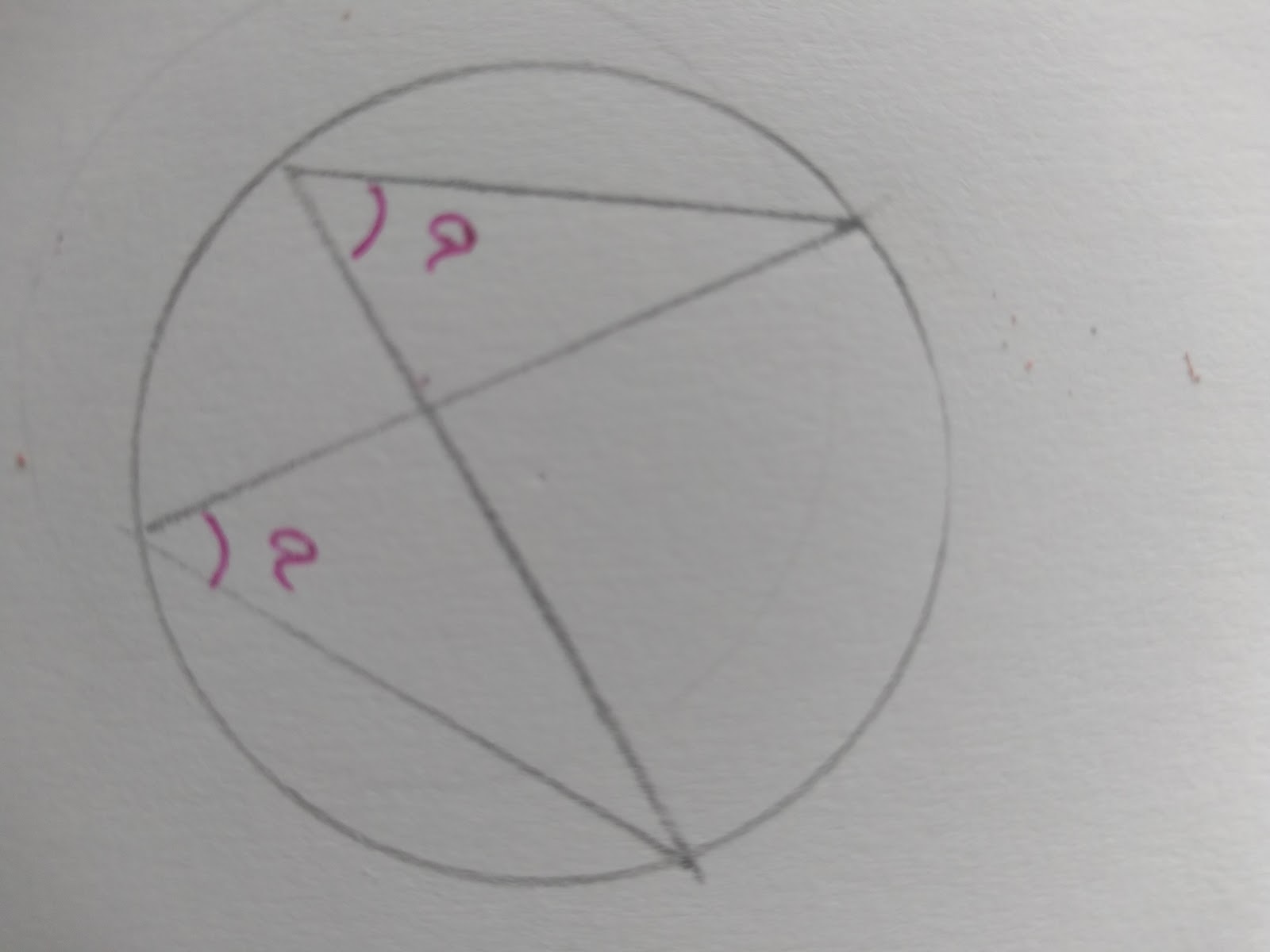
Angles in the Same Segment

These angles are created at same points on a segment. They the angles are therefore equal.

Circle Theorems, figure 1

Think about how you can trace the lines without removing your pen from the page. From the segment to the circumference to the other segment, it creates an identical angle!

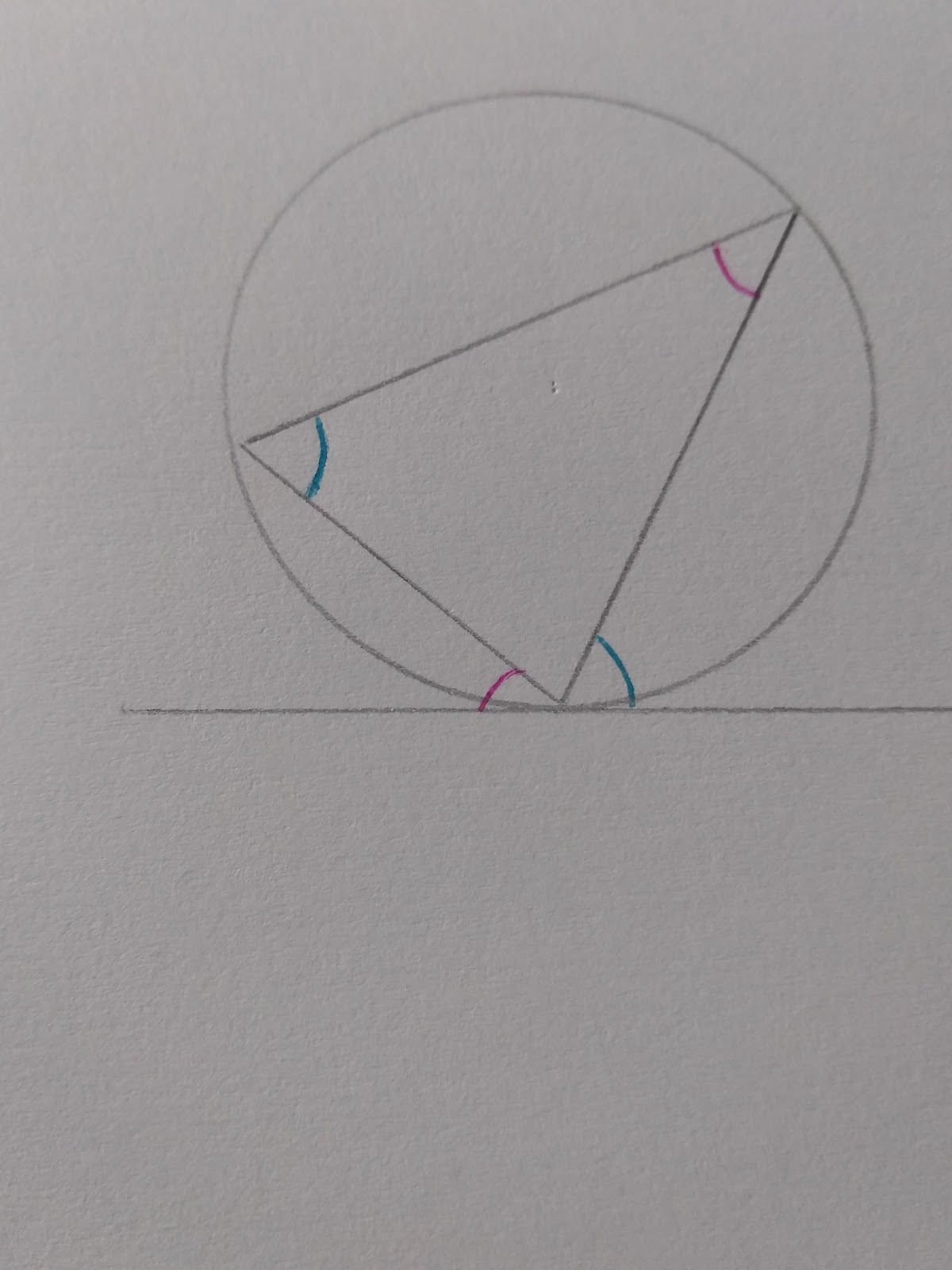
Alternate Segment Theorem

Circle Theorems, figure 1

The key to this theorem is remembering that there are 180 degrees on a straight line and 180 degrees in a triangle.

Therefore if you know two angles on a straight line the missing angle must be 180- the two you know added together. Equally if you know to angles in a triangle the missing angle is 180- the two you know. That’s why this theorem works! Think straight line = angles in a triangle.

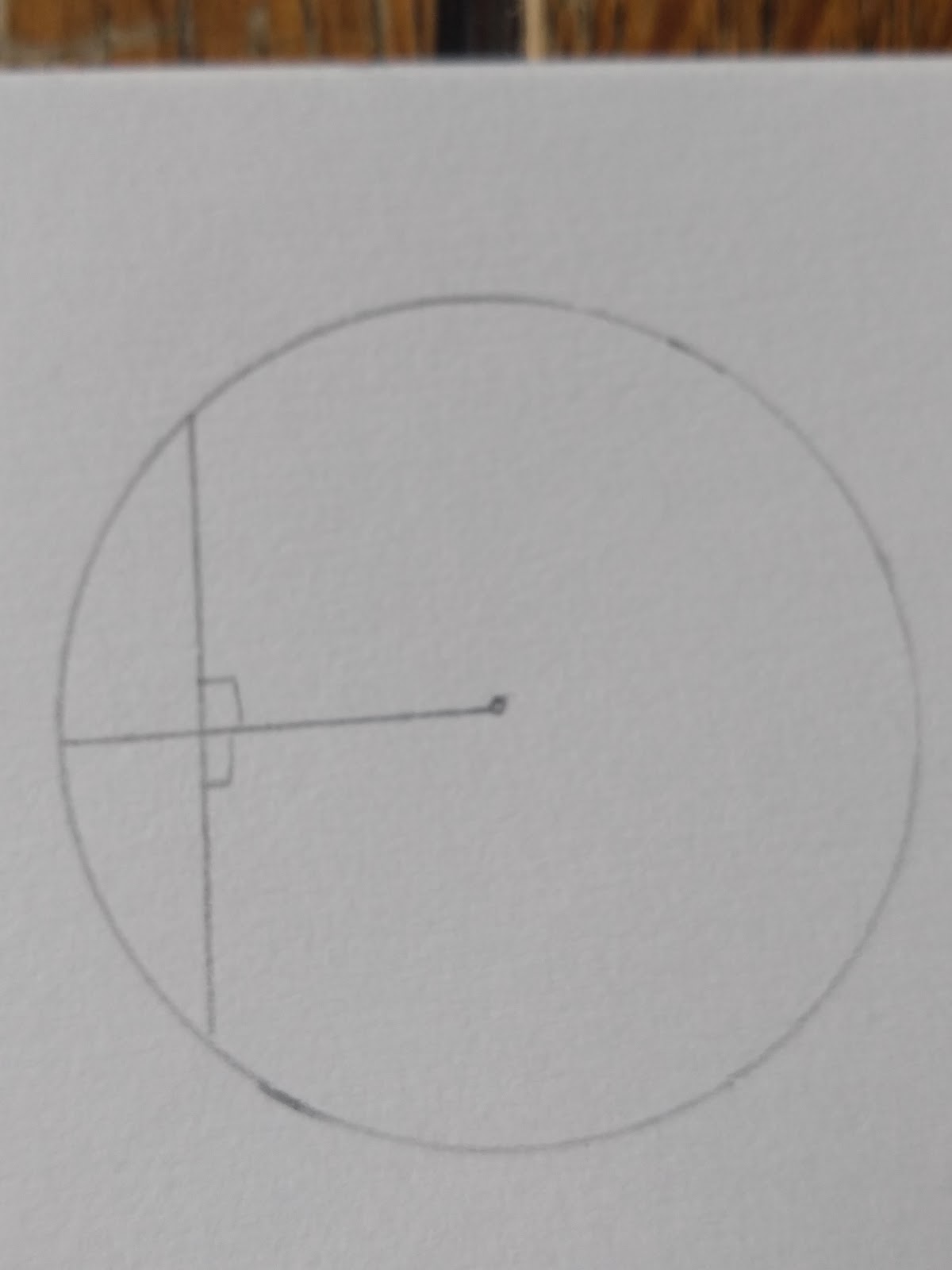
Perpendicular Bisector of Achord

Circle Theorems, figure 1

A line that passes through a chord at a right angle ( the perpendicular bisector), passes through the centre of the circle. This applies to any circle.