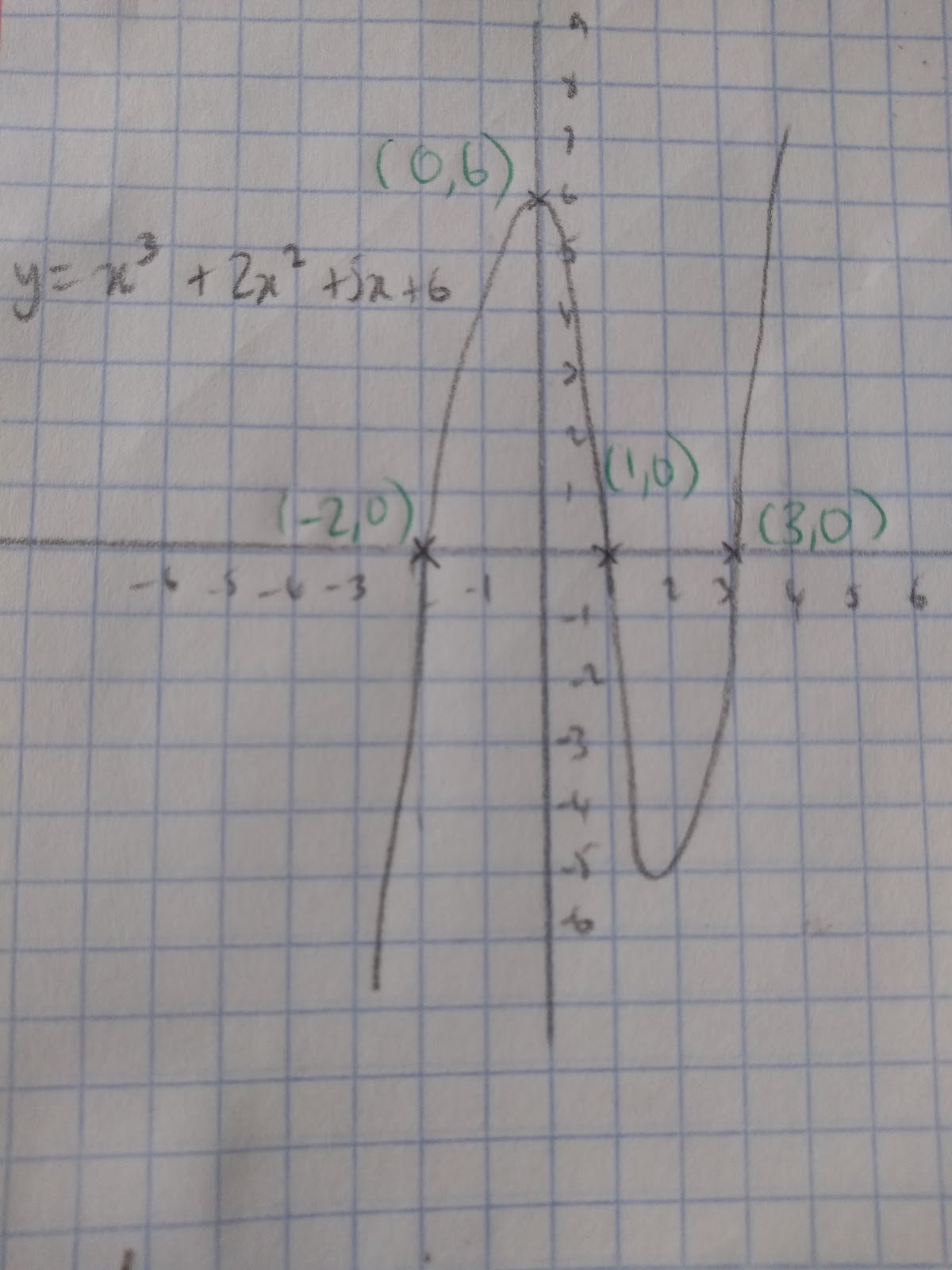Recognise, Sketch and Interpret Graphs

Sketching linear and quadratic functions

When we sketch graphs, there are some important elements that we need to show.

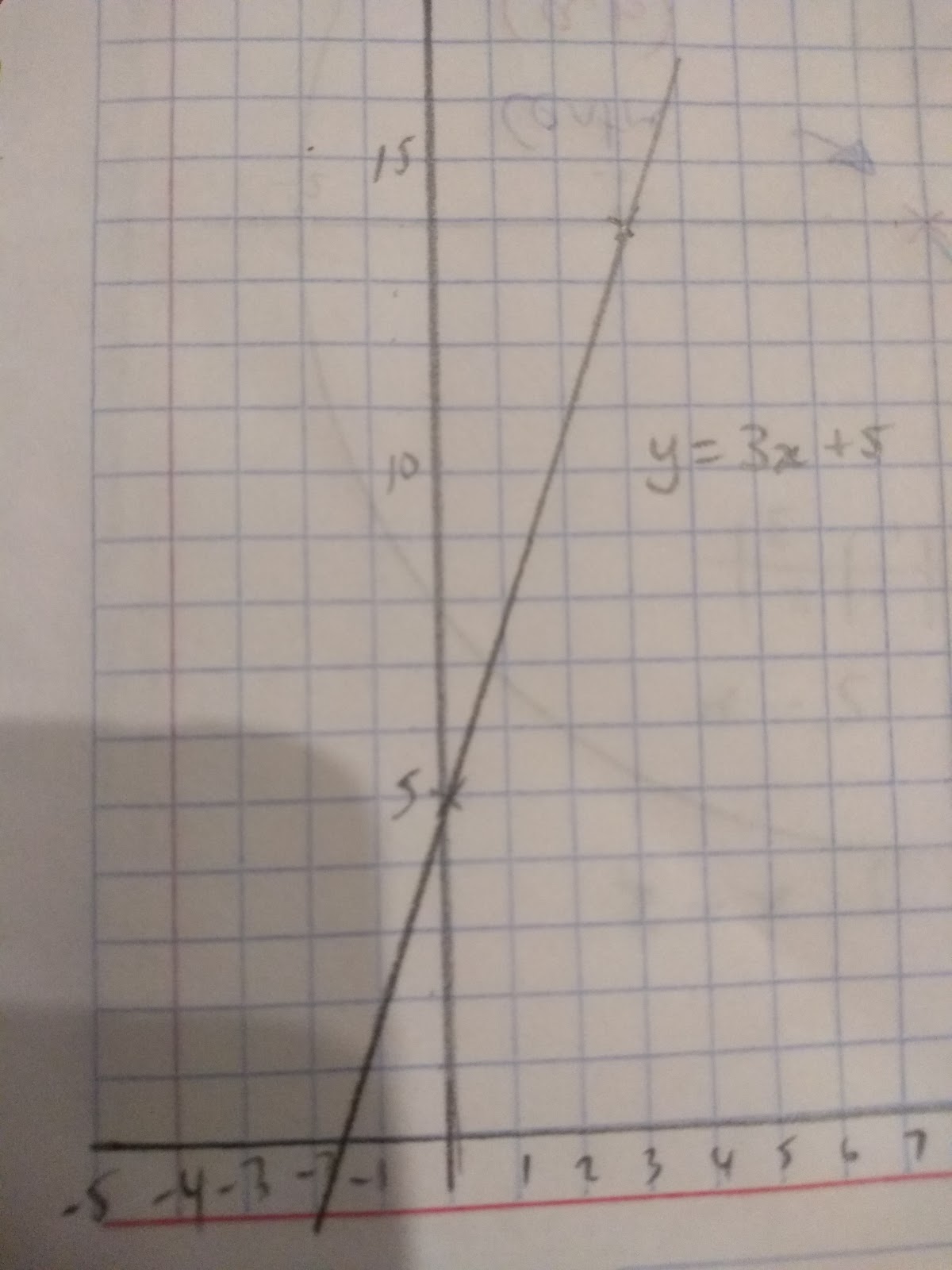
When sketching linear functions, such as y=3x+5 it is important to make sure you have shown:

  1. The y intercept ( where it crosses the y axis)
  2. That you have worked out at least two points
  3. Drawn a straight line through your points with a rule

Eg. Sketch the graph y=3x+5

When x=0, y=3(0)+5. y = 5

When x=3, y=3(3)+5. y=14

So we can plot the points: (0,5) (3,14)

Plot these points and connect them with a straight line.

Recognise, Sketch and Interpret Graphs, figure 1

Sketching Quadratics

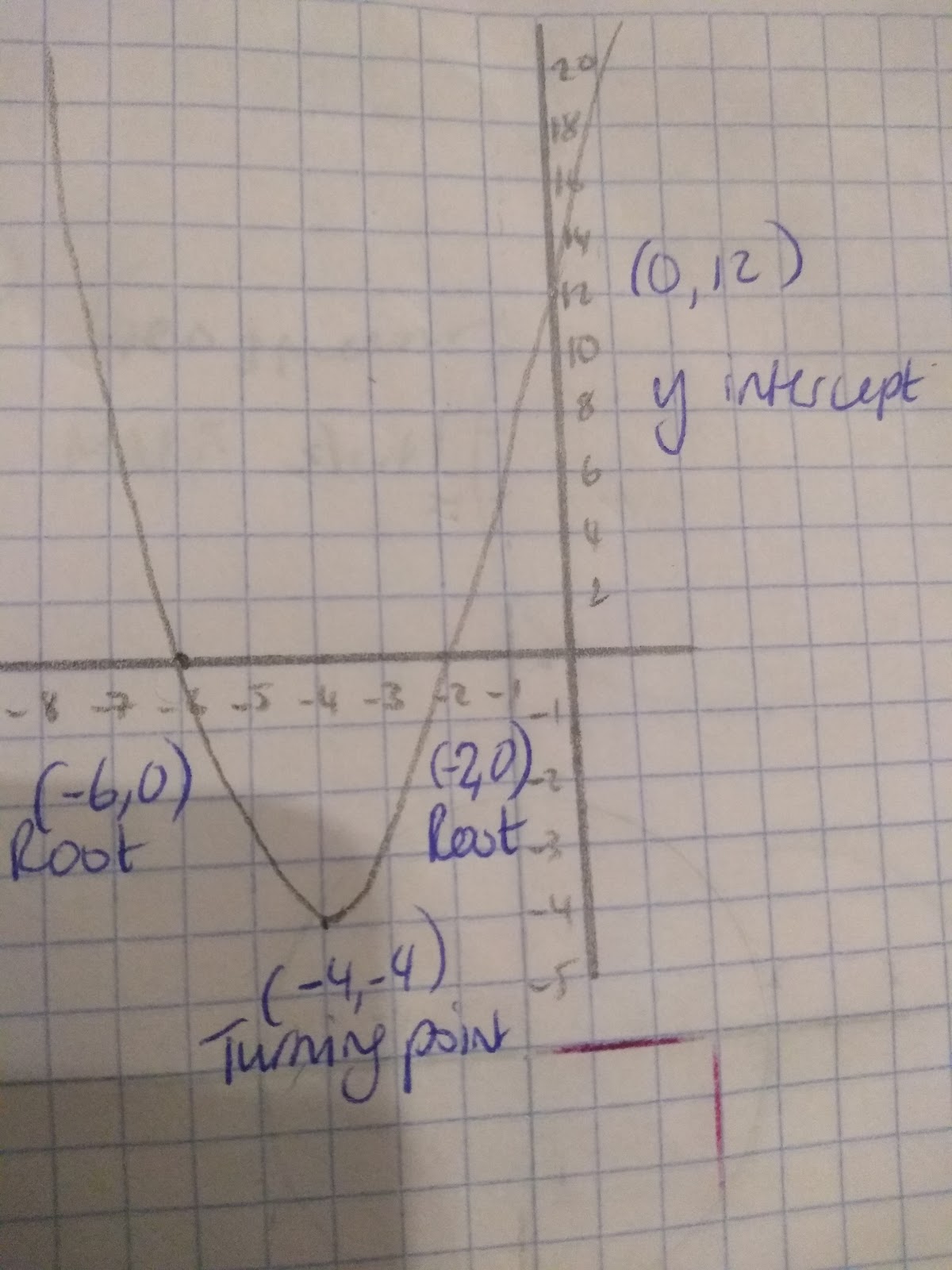
When it comes to sketching quadratics, there are a couple more things that we need to show:

  1. Roots (if there are any)
  2. Turning points
  3. Identify the y intercept
  4. A smooth curve

For example: y= x2+8x+12 or y= (x+2) (x+6)

  1. 0=(x+2)(x+6) therefore the roots will be x=-2 and x=-6
  2. Turning point’s x value is the average of the roots, therefore (-2+-6) ÷2=-4 so the y=-4. (-4,-4) is the turning point.
  3. y intercept is when x=0. y=(0+2)(0+6) =12. (12,0) is the y intercept.
  4. Sketch your graph and make sure you label EVERYTHING!

Recognise, Sketch and Interpret Graphs, figure 2

Sketching simple cubic functions

When it comes to simple cubic functions firstly let’s remind ourselves of what they look like:

Recognise, Sketch and Interpret Graphs, figure 1

y=x3__ y=-x__3

As with quadratic graphs, when we sketch cubic graphs we need to make sure we show certain things!

  1. Roots
  2. Positive or negative shape
  3. Smooth sketch

(Don’t worry about turning points for cubic graphs!)

Step 1: To identify roots we need the equation for our graph to be in the form: y=(x+a)(x+b)(x+c).

For when our equation is in this format, to find the roots we just need to make each bracket= 0

For example, the graph y=(x-1)(x+2)(x-3)

Therefore: x=1, x=-2, and x=3

Recognise, Sketch and Interpret Graphs, figure 2

Step 2: Multiply out the brackets to see if the graph is positive or negative.

y= x3+2x2+5x+6

Sketching trig functions

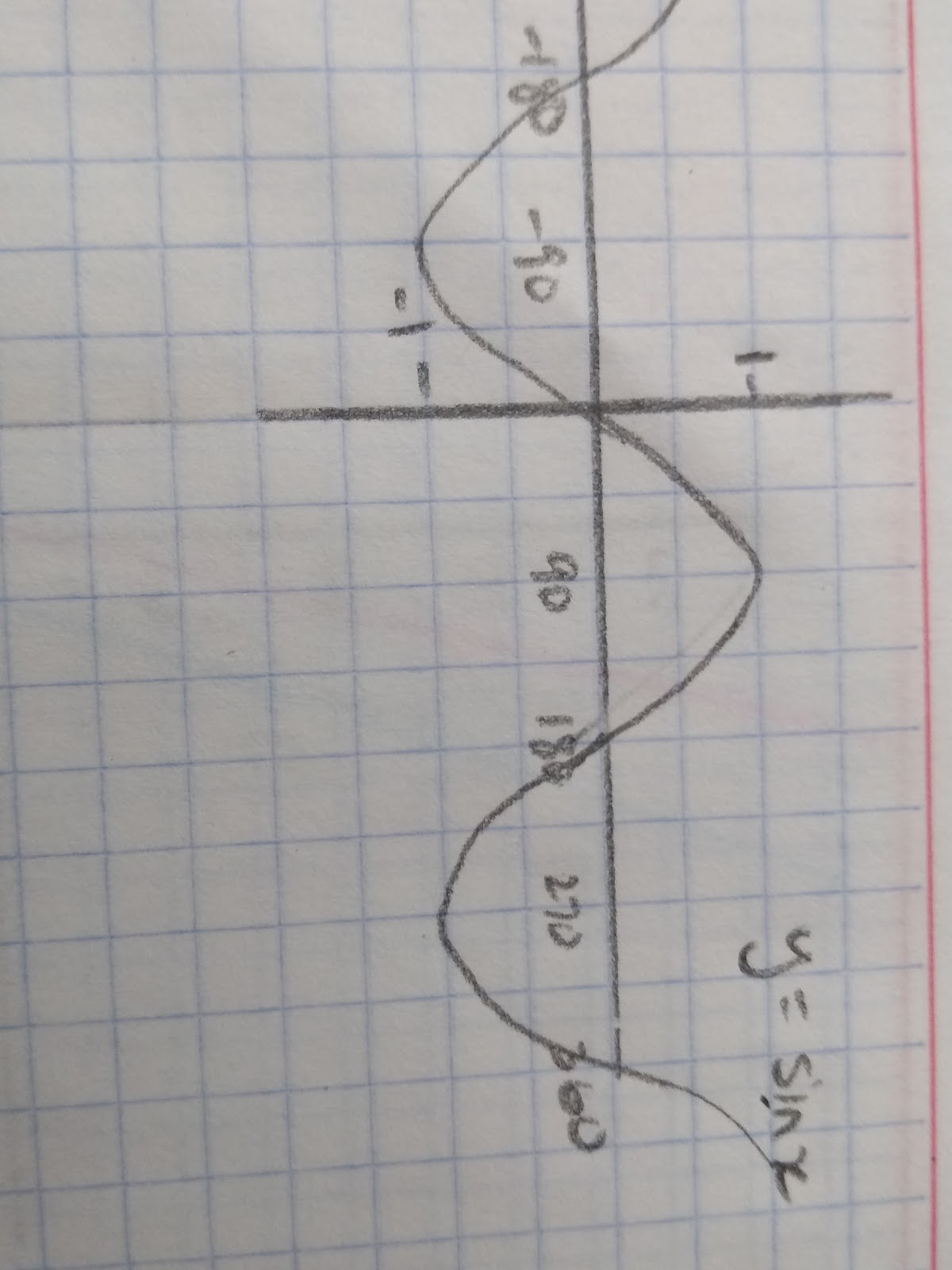
Sine Graph

Recognise, Sketch and Interpret Graphs, figure 1

  • Remember, the sine graph goes from -1 up to 1 and then decreases back to -1.

Cosine graph

Recognise, Sketch and Interpret Graphs, figure 2

  • The cosine graph goes from 1 downwards to -1

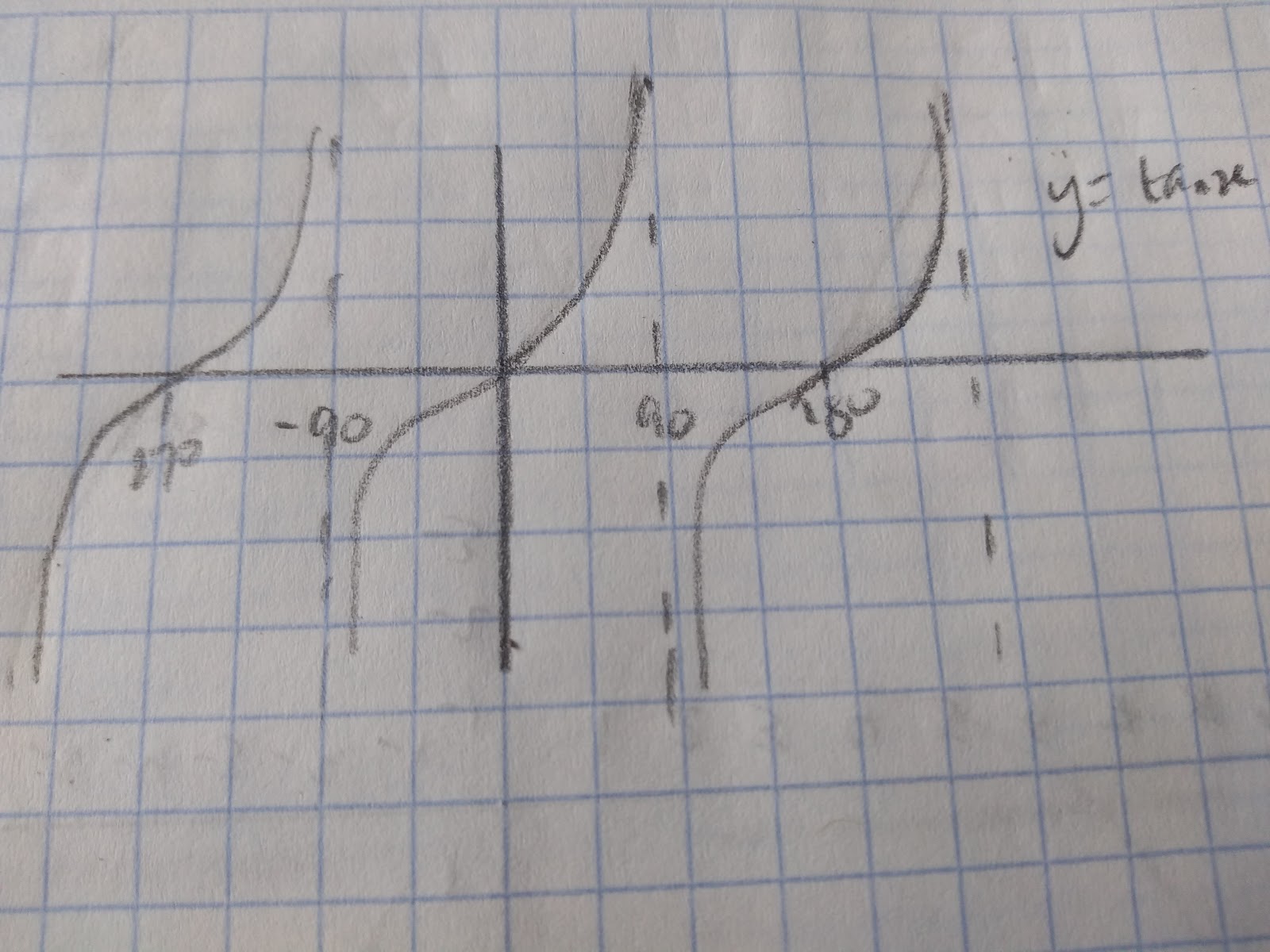
Tan Graph

Recognise, Sketch and Interpret Graphs, figure 3

  • The graph of tan x is not a wave!
  • You need to know the fundamental elements of each graph, where they cross the y axis, the x axis and the shape.
  • Remember sketches estimate. When you read values from a graph that you have sketched the answers will not be exact.
  • You may also be required to read values from trigonometric graphs. Remember always use a ruler to help you read values from a graph! Depending on the axes these values may be in terms of pi or radians.
What are the roots of (x+3)(x-4)(x-2)?
Your answer should include: -3 / 4 / 2
What do you need to show on a sketch of a quadratic graph?
Your answer should include: Roots / Turning Points / Smooth Curve / y Intercept