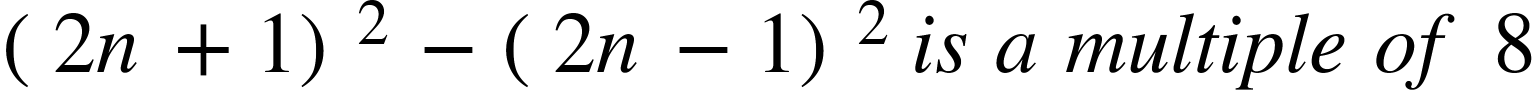Proving and Disproving Equivalence
Equations and identities
Knowing the difference between an equation and an identity is very important. Remember the definitions: An equation shows two things that are equal to each other. Whilst an identity is true WHATEVER the number of the variable. Here are some examples to help:
Equation: 5x = 5. This is only true when x = 1.
Identity: 5x = x + 4x. This is true for every the value of x.
Equation: 3x + 2= 8 x -6. This is only true when x = 1.6
Identity: 3 + 7y = 2 + 1 + 5y + 2y. If you collect the like terms you will find both sides simplify to 3 + 7y.
Equation: 5(x + 3) = 10. This is only true when x = -1.
Identity: 5(x + 3) = 5x + 15. Expand the brackets and you will find exactly the same expression on the other side.
Manipulate to show expressions are equivalent
Sometimes we will have to manipulate, simplify or expand expressions to show that they are equivalent. To do this we need to know the different forms that calculations can take. In these questions you will often be shown two expressions and asked to show how they are the same. Making sure you show clear working out is essential as you need to communicate to the examiner that you know exactly what you are doing. Example:
Proofs
When it comes to proving things in maths you need to show that you can use facts, given or known truths ( eg. a square has four sides) to construct an argument. Most of the time this will involve showing (proving) if something is or isn’t true.
You may be asked to disprove something which you can do by finding one counter-example.
When it comes to algebraic proofs, remember that you need to find ways of generalising things. Key numbers that can be generalised:
Generalising different types of numbers:
Even numbers = 2n
Odd numbers = 2n + 1
An example question:
We know that 8n is a multiple of 8 as it is 8 multiplied by a number, the very definition of a multiple.
- Is this an identity of an equation? 6(x + 3) + 5 = 6x + 23
- Your answer should include: Identity / Yes