Surface Area

Spheres

The area of each face on a 3D shape, added together, is called the shape’s surface area.

The formula required to work out the surface area of a sphere is: 4πr²

For the sphere above: = 4πr²

= 4π(8)²

= 216π

= 678.58 cm²

Cones

The formula to find the surface area of a cone:

Pyramids

To find the surface area of a pyramid once again, work out the area of each face and add them together.

A square based pyramid has:

Square base: 5 x 5

4 x triangle: 4(15 x 5 x 1/2)

Added together = 150 cm²

Prisms

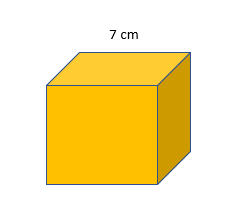
Cubes:

To work out the surface area of a cube, work out the area of one face and multiply it by 6 as a cube has 6 faces of equal area.

In this case the cube’s surface area =

1 face= 7x7

6 faces= 6(49)

= 294 cm²

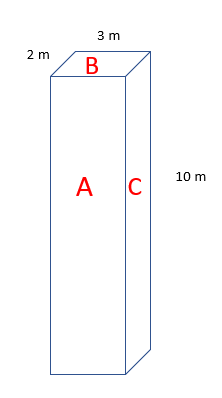
Cuboids:

To out the surface area of a cuboid, remember that it has three different sides:

A= 3 x 10 = 30

B= 2 x 3 = 6

C= 10 x 2 = 20

2(A+B+C) =

2(30 + 6 +20) =

2(56) = 112 m²

You need to remember that there are also 3 sides that you can’t see - that’s why we multiply by 2.

Other prisms:

The most important part of finding the surface area for 3D shapes is to make sure that you have taken into account every face on the prism!

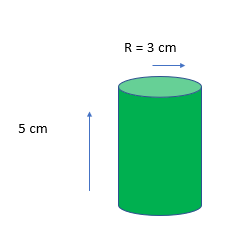
For example, with a cylinder, remember you have 2 circles and one rectangle, whose width is actually the circumference of the circle:

Circle= π x r x r

= π x 3 x 3

= 9π Remember there are 2 circles!

Circles x 2 = 18π

Rectangle: length x circumference of the circle

= 5 x π x 6

= 30π

Total = 30π + 18π = 48π = 150.80 cm²

Composite Shapes

To find the surface area of composite shapes, break down the shape into different faces, work out their area and add them together.

For example, in this shape you would need to split it into two cuboids but think carefully about the faces that are showing and only add those together!

The surface area of a cube is 294 cm^2. What is the length of each side.

Your answer should include: 7cm / 7

A cuboid has dimensions 5 cm, 6 cm and 7 cm, what is its surface area?

214