Measuring

Measuring line segments

Often on a coordinate grid you will required to find the length between two points, or in other words, the length of a line segment. Line segments are parts of a line and are denoted by two letters, eg. line segment AB.

When it comes to line segments we often:

1. Want to find their length
2. Want to find their mid-point.

So to find the length of a line segment we need to remember our good friend pythagoras. For if we draw two lines, one vertical the other horizontal, we create a right angle triangle. Then we can use Pythagoras to work out the hypotenuse, which is our line segment.

Here’s how to do it step by step:

1. Step 1: Work out the length of the vertical distance between the points (y1-y2)
2. Step 2: Work out the length of the horizontal distance between the points (x1-x2)
3. Step 3: Use pythagoras to work out the length of the hypotenuse:

(y1-y2)² + (x1-x2)² = hypotenuse²

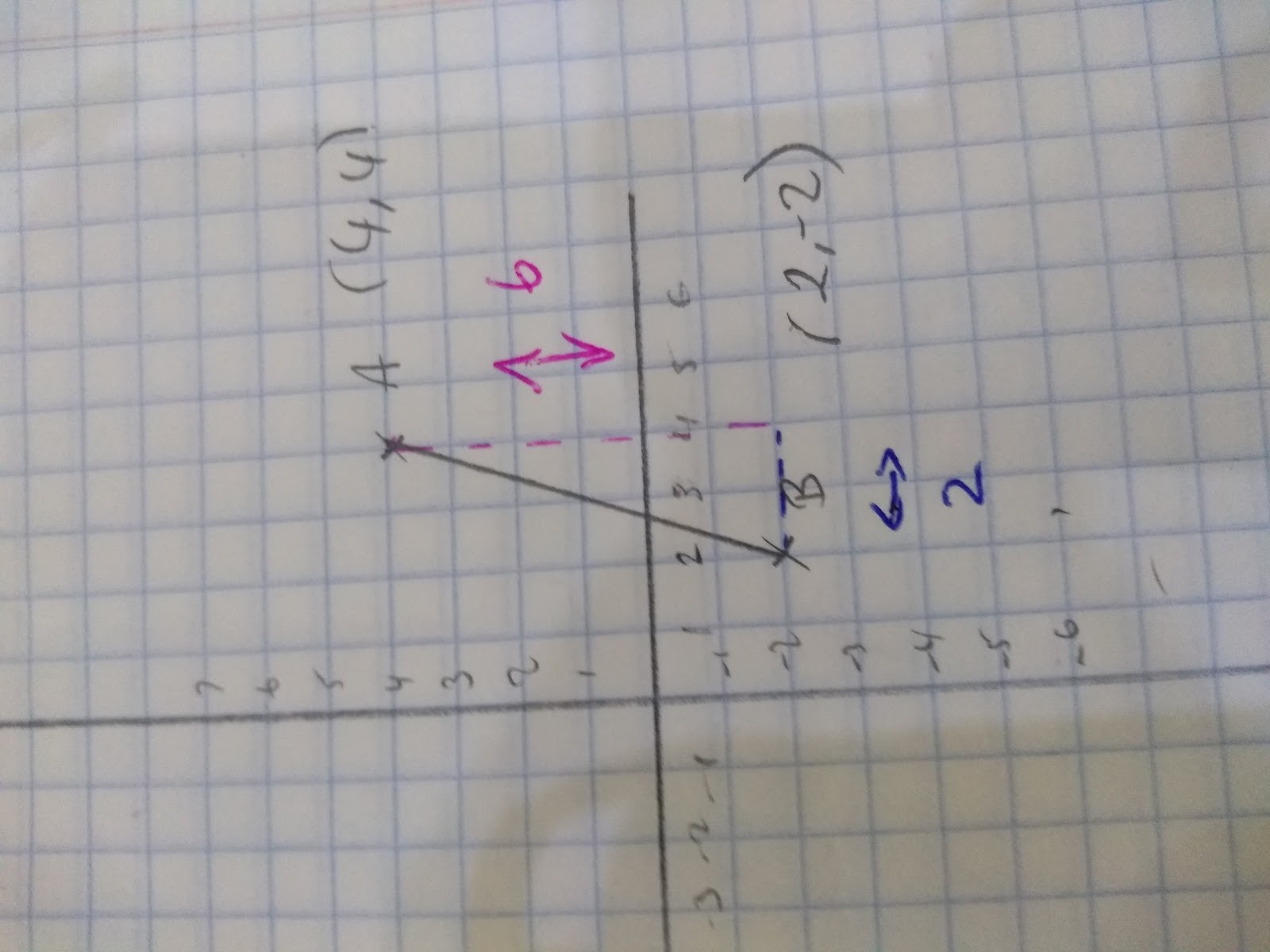
For example with the line segment AB we can follow the steps below. Sometimes it helps to label the coordinates first.

(4,4) (2,-2)

(x1,y1) (x2, y2)

1. Step 1: (y1-y2) = (4 –2)= 6
2. Step 2: (x1-x2) = (4 -2) = 2
3. Step 3: (y1-y2)² + (x1-x2)² = AB²

(6)² + (2)² = AB²

36 + 4 = AB²

40 = AB²

__√4__0 = AB

= 6.32 (to 2 d.p)

2) Finding the midpoint of a line segment

To find the half-way point between two coordinates you need to find the average of the x coordinates and the y coordinates. So it’s quite simple:

1. Step 1: Add the x coordinates together and divide by 2 to find your x coordinate.
2. Step 2: Add the y coordinates together and divide by 2 to find your y coordinate.
3. Step 3: Write the (x,y) in coordinate form.

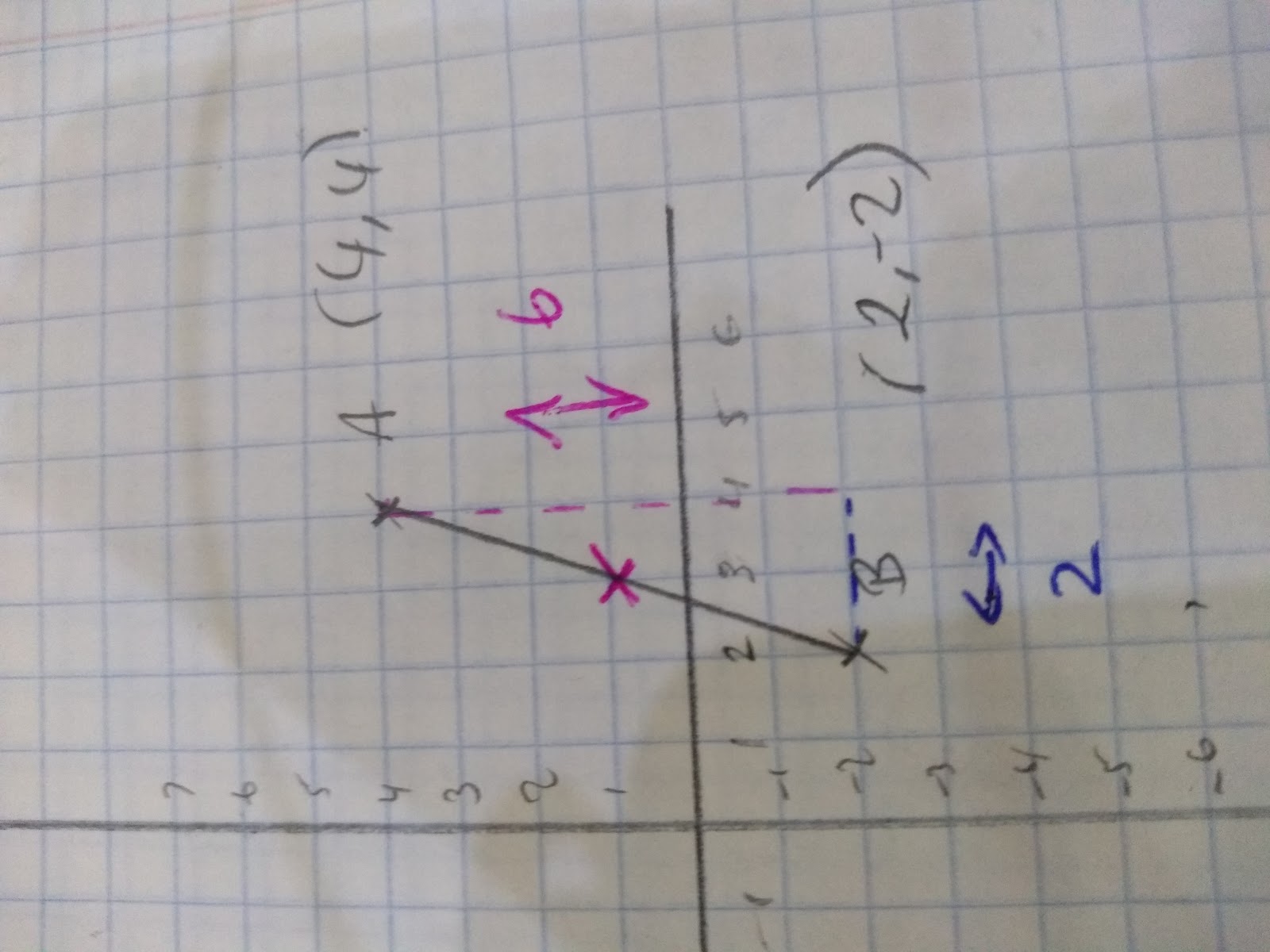
Eg. Line segment AB has the coordinates:

(4,4) (2,-2)

(x1,y1) (x2, y2)

Therefore:

1. Step 1: (x1 + x2)/2 = (4 + 2)/2 = 3
2. Step 2: (y1 + y2)/2 = (4 +-2)/2 = 1
3. Step 3: (3,1)

Measuring Angles

When it comes to measuring angles, most of the time you will be expected to prove the angles from axioms, i.e. known facts. For example, angles in a triangle sum to 180 degrees or (n-2) x 180= the total amount of angles in a polygon.

However, you may also be required to measure an angle with a protractor.

When measuring angles make sure that you line up the protractor carefully and check that you are measuring from 0. On most protractors there are two scales so make sure you read the correct scale! Also check, you know a right angle is 90 degrees and 180 degrees is a straight line! Use these facts to help you check.

Interpreting Maps

Being able to interpret scale factors and measure line segments are skills often used in real life with maps.

You may be given a map, two points and a scale factor. Using your ruler and the information given you will need to work out the length. To do this simply :

1. Measure the difference with your ruler
2. Multiply by the scale factor

In this example the distance between points A and B is 6.5cm .

The scale factor is 1:4000, this means 1 cm on the map represents 4000 cm in real life.

Therefore 6.5 x 4000 =26,000 cm

The likelihood is that you will need to convert 26,000 into m, divide by 100 = 260 m or 0.26km

Bearings

Often we will want to measure the angles between different points, or the bearing of one point to the next. Sometimes you will need to work out the angle of certain bearings or give the bearing of one point to the next.

Important facts to remember about bearings:

1. There will always be three digits eg. 023 = 23 degrees or 157 = 157 degrees
2. Always measure from the north
3. Always measure in a clockwise direction.
4. Check your language - if you’re measuring a bearing of A from B- your north line will start from B!

So, how to work out the angle between two points:

1. Step 1: Draw a line between the points
2. Step 2: Draw your north line
3. Step 3: Mark on the angle you need to measure
4. Step 4: Measure the angle, remember a straight line is 180 degrees to help you.

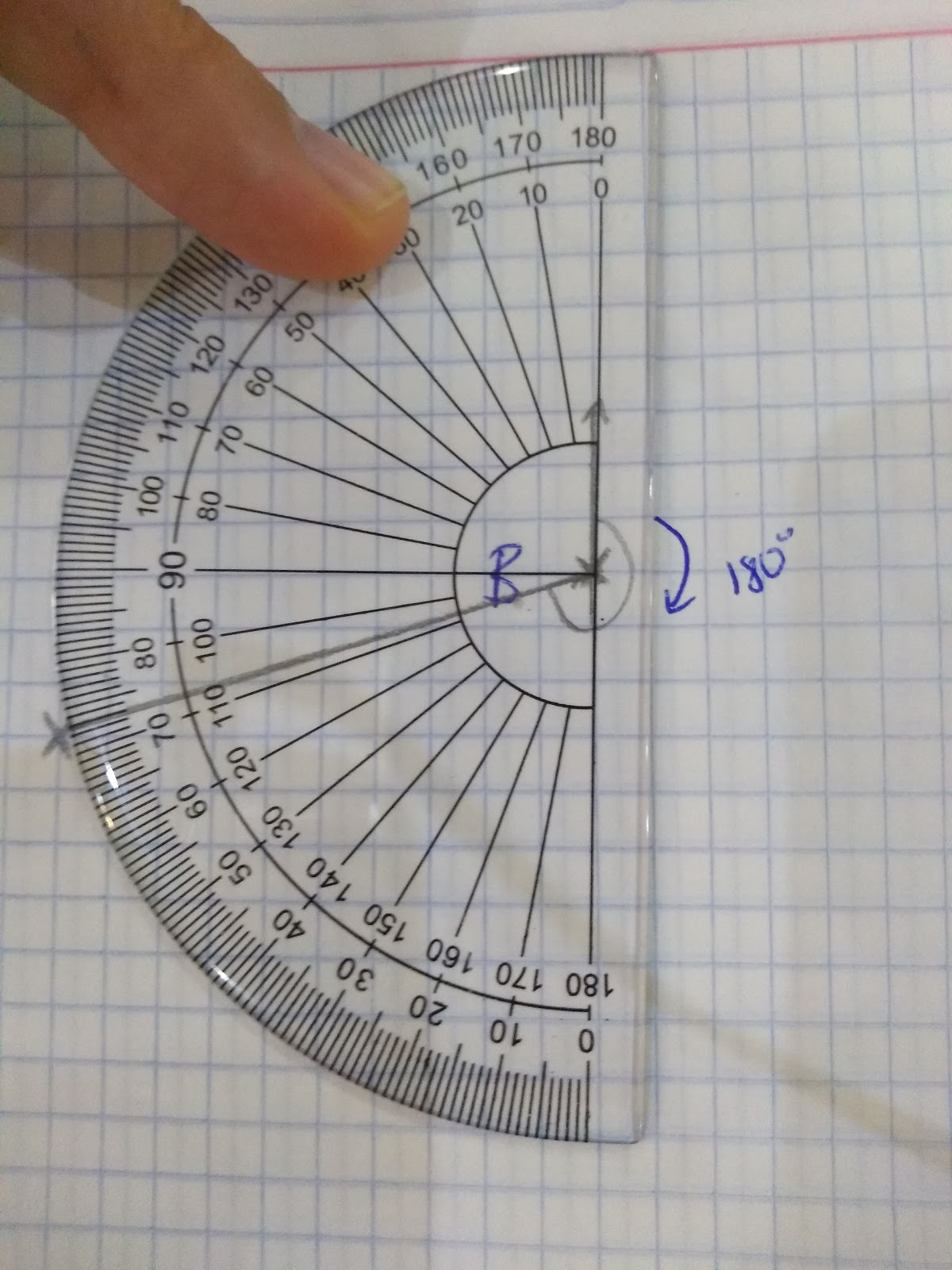
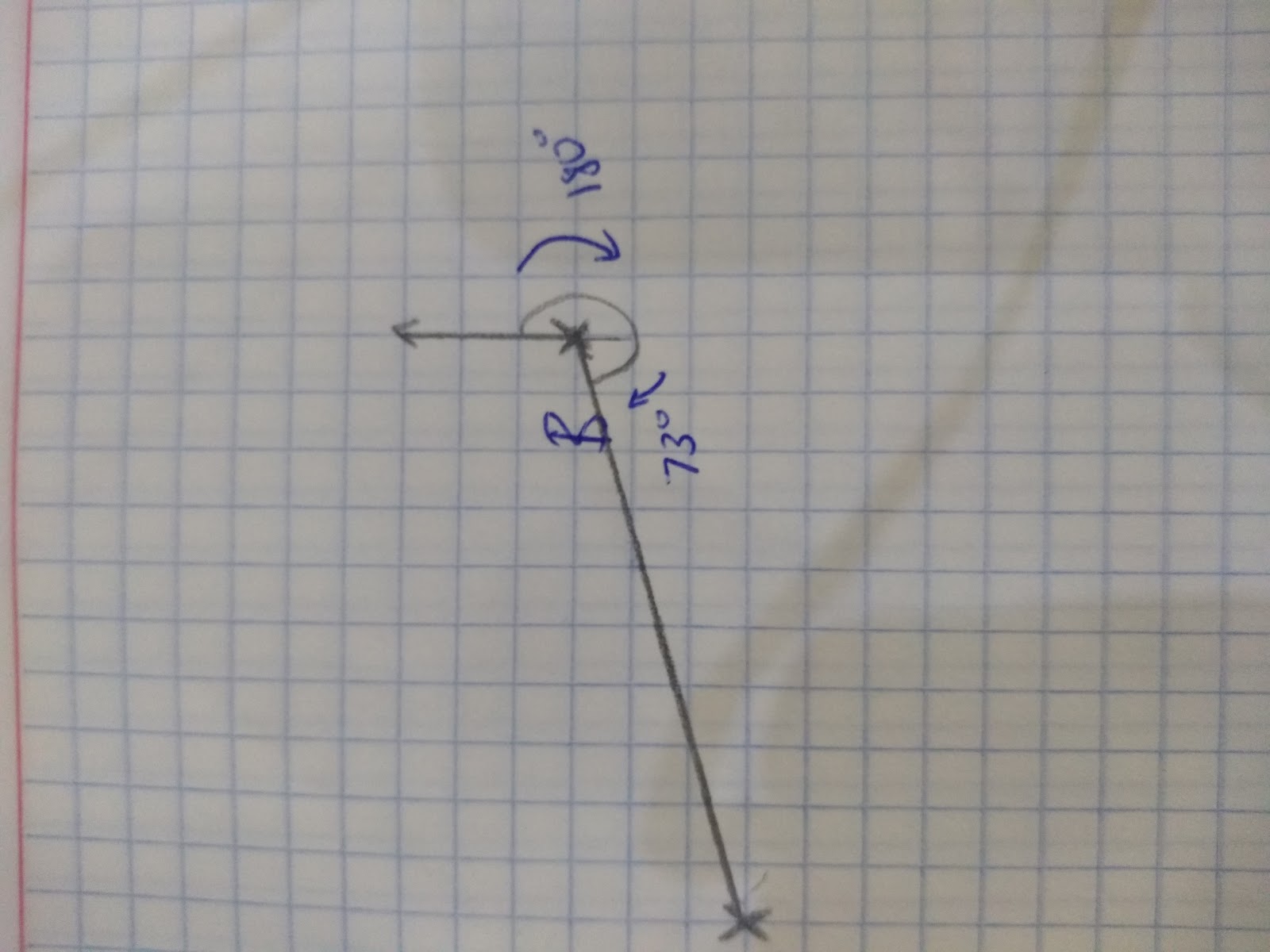
Eg. In the example below I know that from the north to the south is 180 degrees, therefore I only need to measure from south to B, in this case that means 73 degrees. Therefore to find out the total bearing 180 + 73 = 253

Sometimes you will need to use your knowledge of bearings to work out missing points.

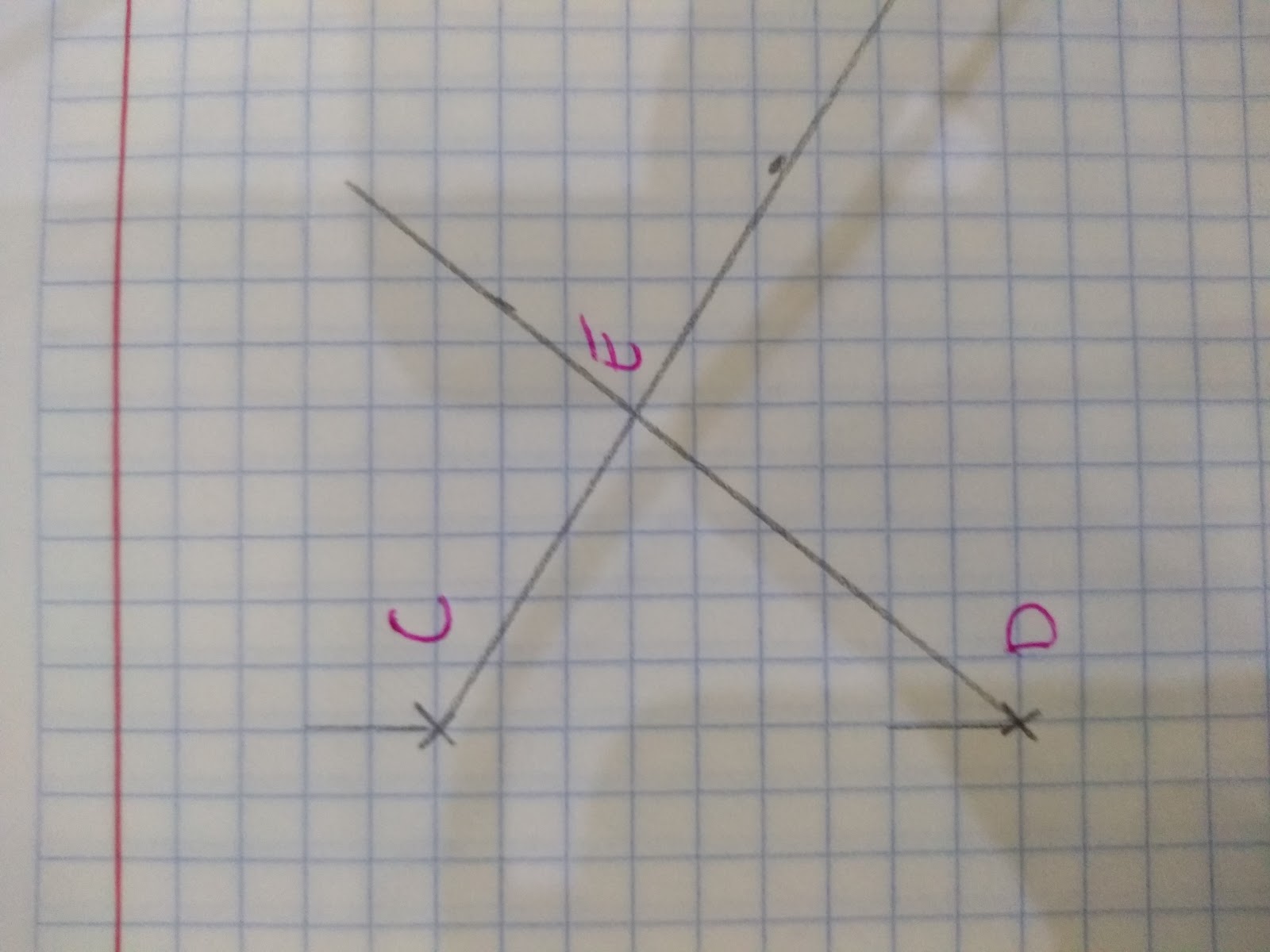
Eg. Point E is at a bearing of 120 from point C and is at a bearing of 040 from point D. Show where Point E is on the map.

1. Step 1: Draw the bearing from point C
2. Step 2: Draw the bearing from point D
3. Step 3: Where the lines cross will be point E- make sure the lines drawn are long enough!

Be prepared to use trigonometry and rules in parallel lines to work out bearing problems in the higher paper. BUT never forget the key principals- 3 digits, measure from north and always clockwise!