Identifying Roots and Turning Points of Quadratic Functions

Identifying Roots

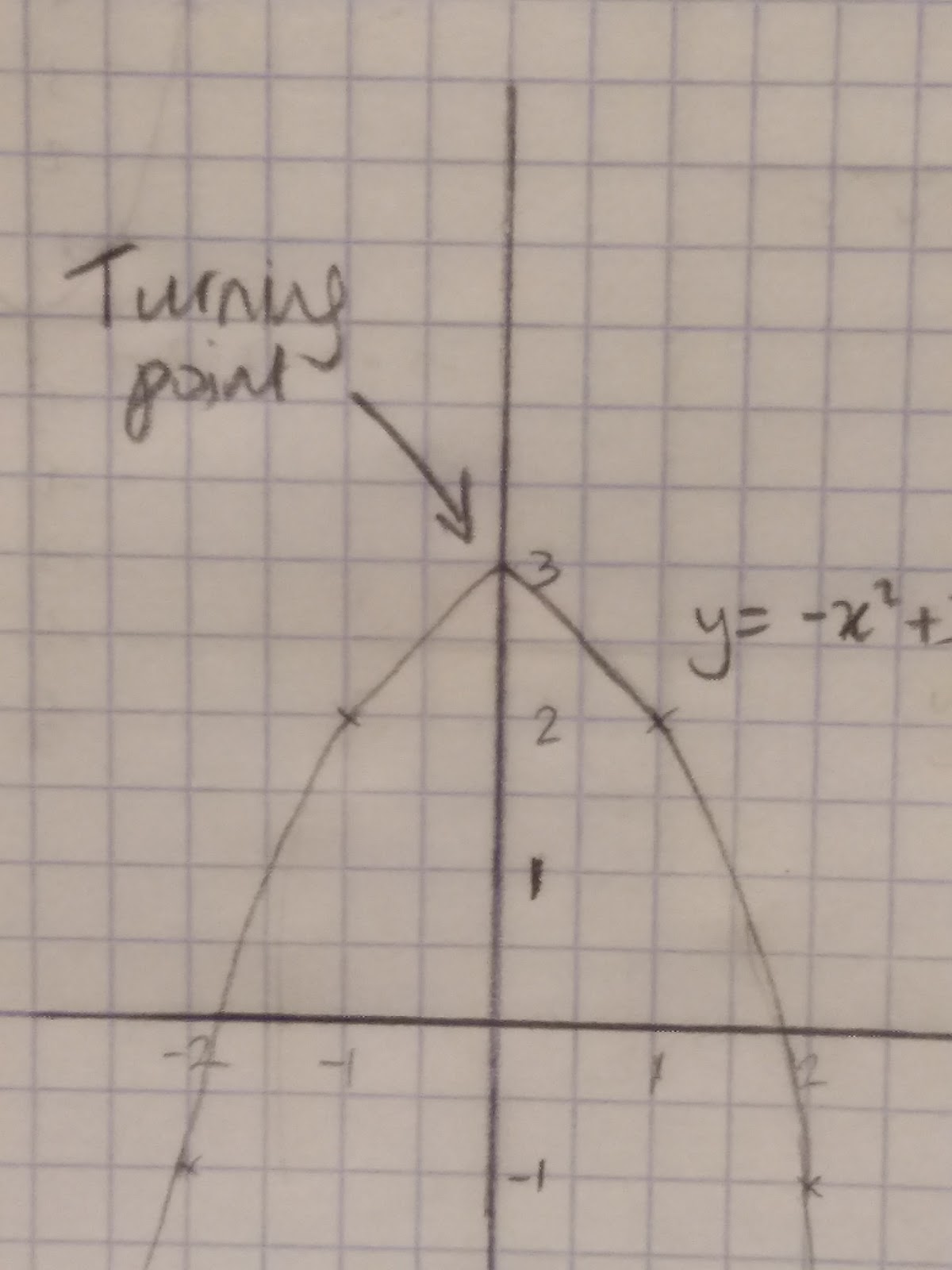
Quadratic graphs tend to look a little like this:

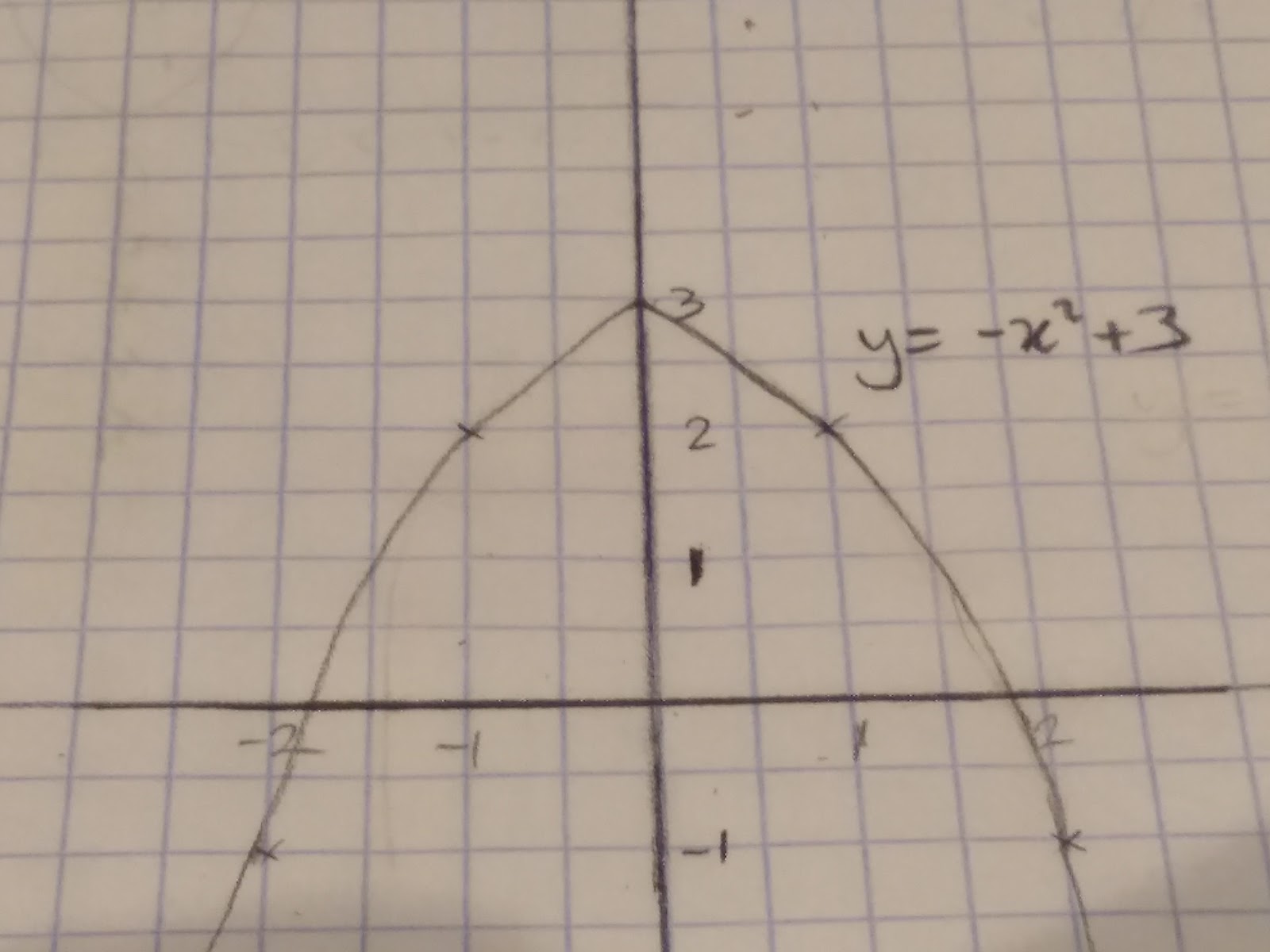
y= -x²+3

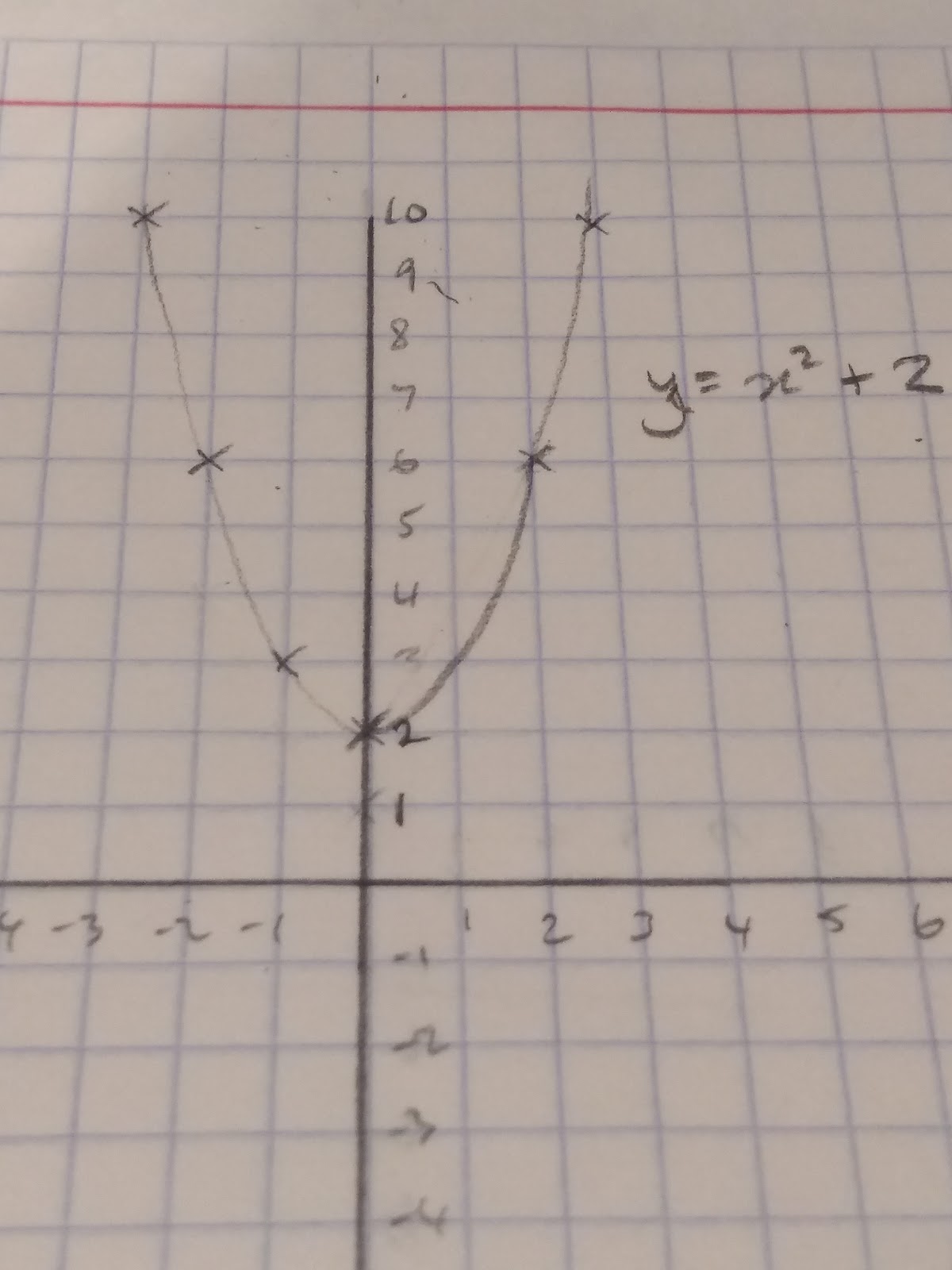
y=x²+2

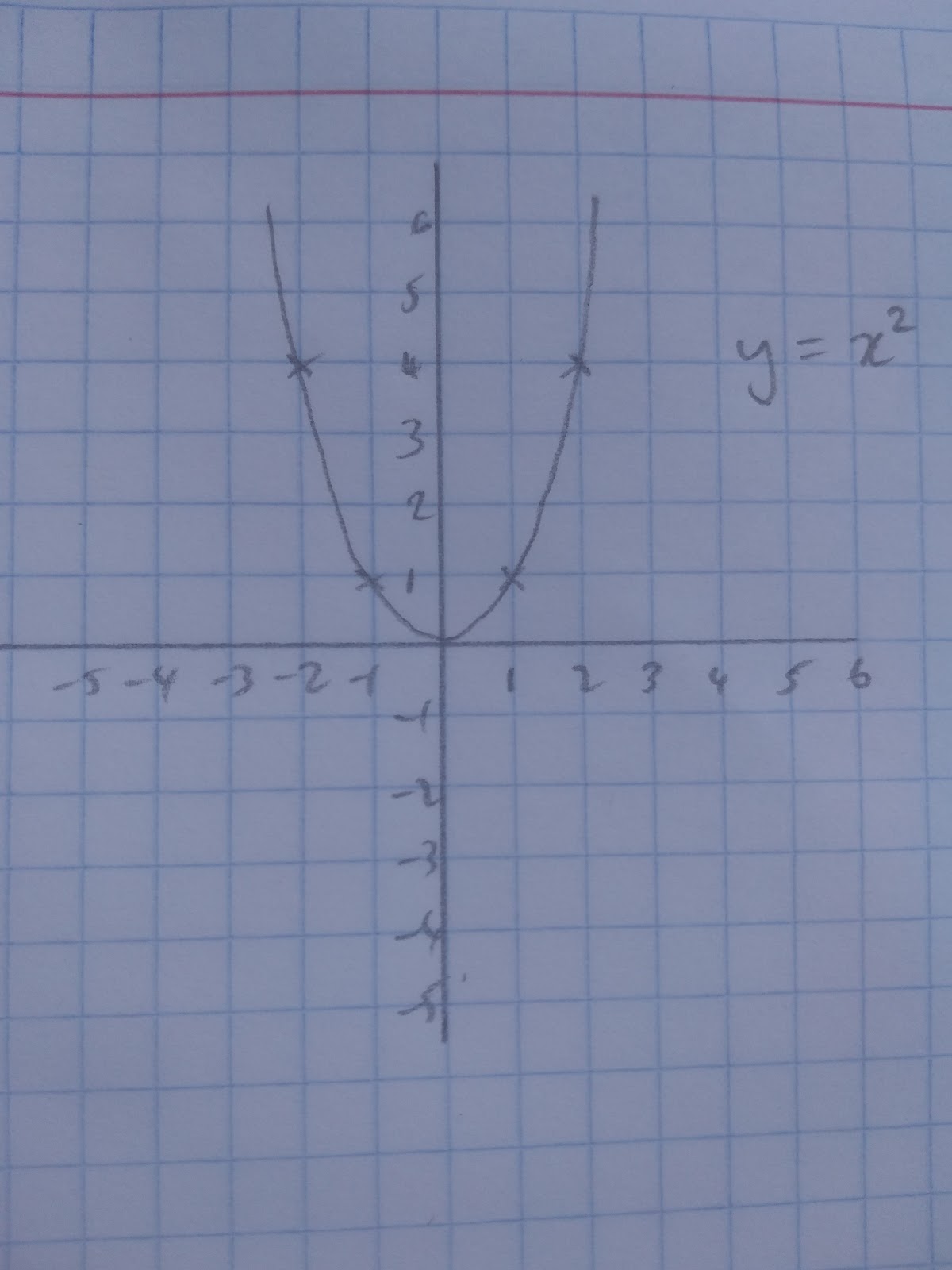
y=x²

All of these equations are quadratics but they all have different roots. But what is a root??

A root is the x value when the y value = 0. It’s where the graph crosses the x axis. Because y=x2+2 does not cross the x axis it does not have any roots. This is easy to see graphically! Equally if we have a graph we can simply read off the coordinates that cross the x axis to estimate the roots.

To work this out algebraically however we use part of the quadratic formula: b2 -4ac

If b² - 4ac = 0 then there will be one real root, one place where the graph crosses the x axis eg. y=x²

If b² - 4ac > 0 There will be two real roots, like y= -x²+3

If b² - 4ac < 0 there won’t be any real roots, like y=x²+2

We can show this algebraically as well:

Remembering that ax²+ bx + c is the standard format of quadratic equations.

For y=x² a= 1 b=0 c=0

b² - 4ac

0² - 4(1)(0) = 0

0 - 0 = 0 therefore there is one real root.

For y = -x² + 3 a=-1 b=0 c=3

b² - 4ac =

0² - 4(-1) (3) = 12

12 >0 so there are two real root.

For y=x²+2 a=1 b=0 c=2

0² - 4(1) (2) = -12

-12 < 0 therefore there are no real roots.

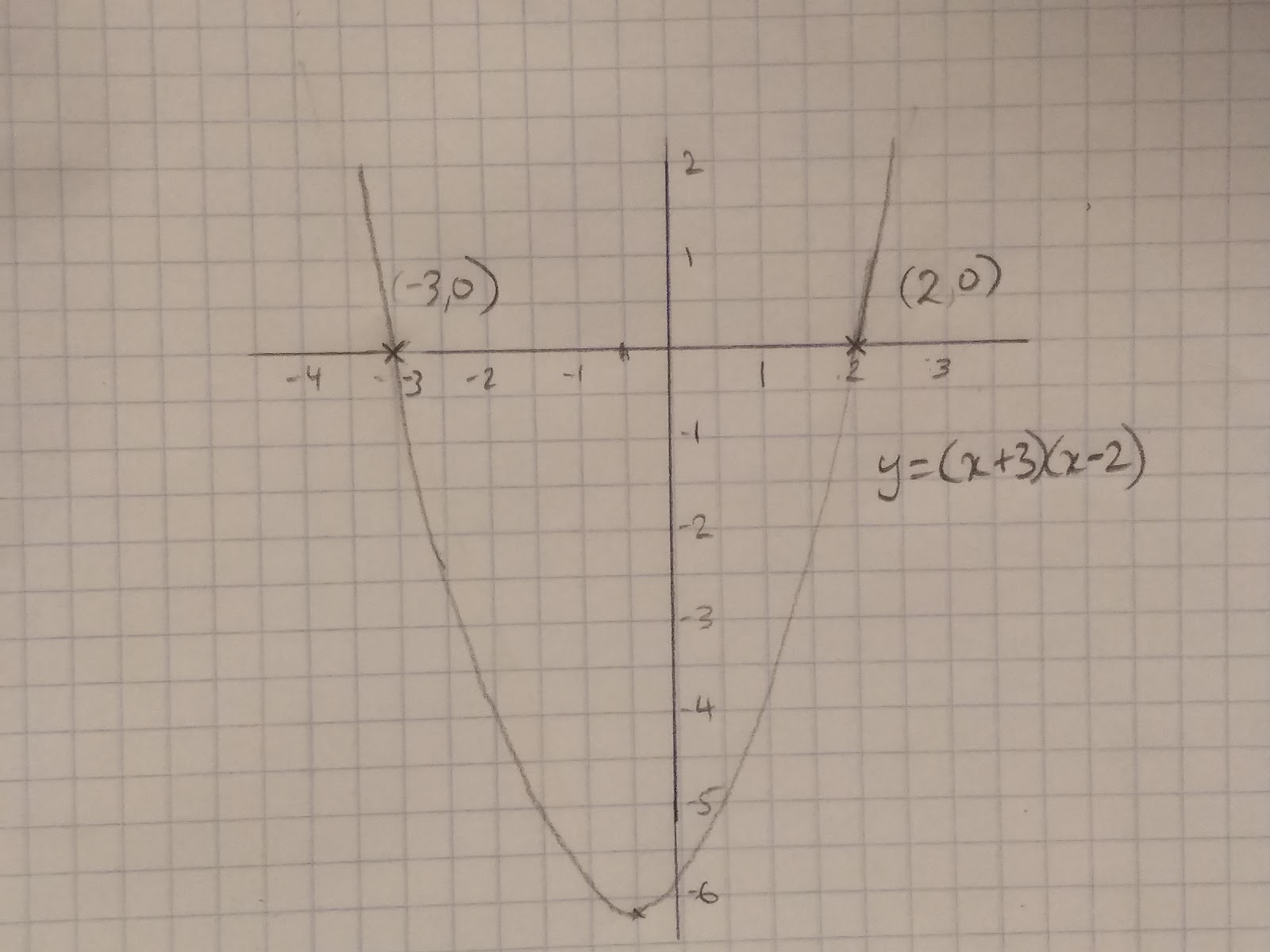
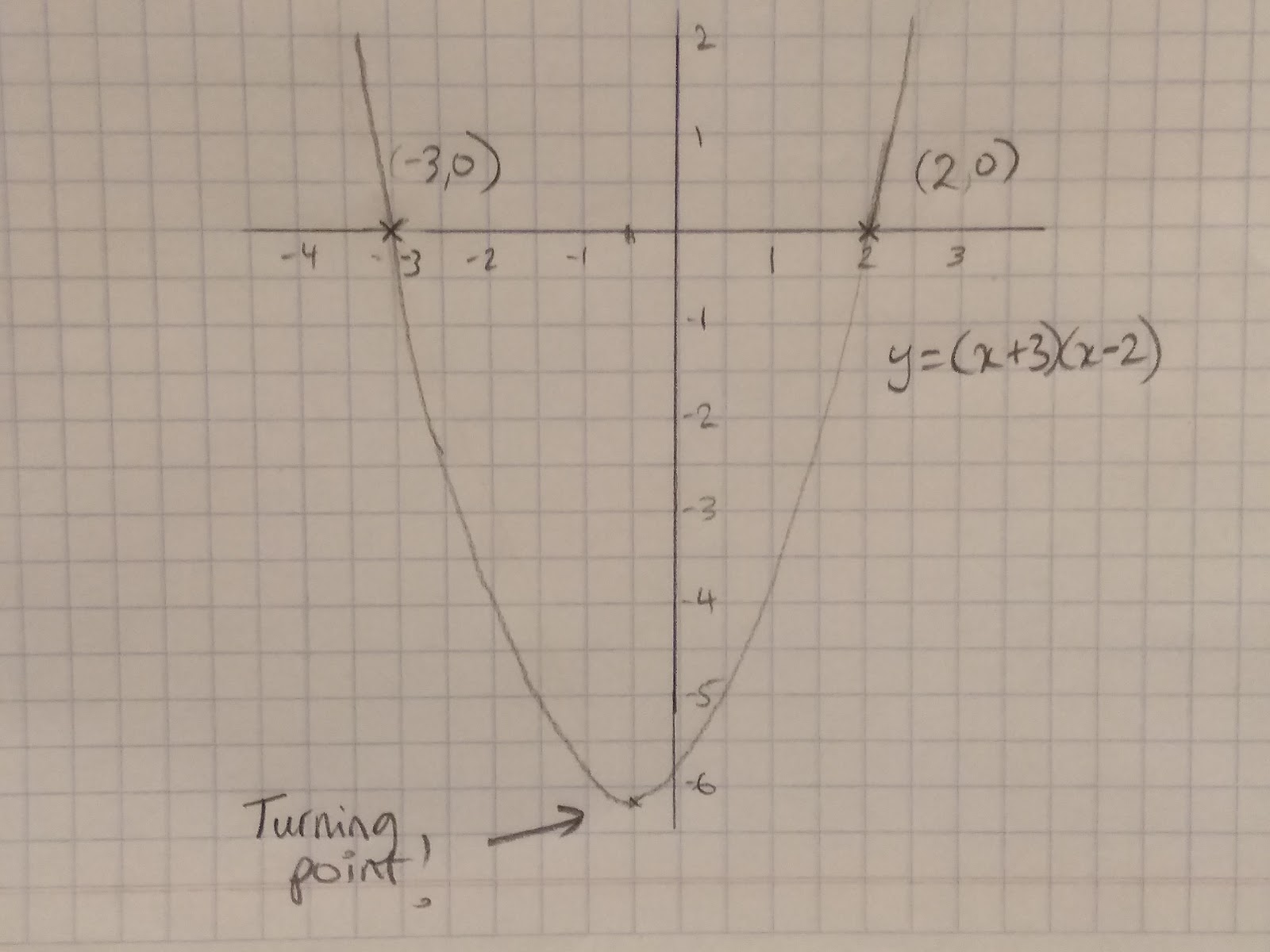
Given that the roots are where the graph crosses the x axis, y must be equal to 0. With this knowledge we can find roots of quadratic equations algebraically by factorising quadratics. For example, if we have the graph y = x² + x + 6, to find our roots we need to make y=0.

Therefore 0 = x² + x + 6

Factorise 0 = (x+3) (x-2)

So each bracket must at some point be equal to 0

0 = (x+3), -3 = x

0 = (x-2), 2 = x

Which is exactly what we can see here:

Identifying turning points

The turning point of a graph is where the curve in the graph turns.

The turning point will always be the minimum or the maximum value of your graph.

To find the turning point of a quadratic equation we need to remember a couple of things:

1. The parabola ( the curve) is symmetrical
2. If we know the x value we can work out the y value!

So remember these key facts, the first thing we need to do is to work out the x value of the turning point. Let’s work it through with the example y = x² + x + 6

Step 1: Find the roots of your quadratic- do this by factorising and equating y to 0. (Exactly as we did above with Identifying roots)

Therefore 0 = y = x² + x + 6

Factorise 0 = (x+3) (x-2)

So each bracket must at some point be equal to 0

0=(x+3), -3= x

0=(x-2), 2=x

Step 2: Find the average of the two roots to get the midpoint of the parabola. This will give us the x value of our turning point!

-3 + 2 / 2 = -½

Therefore x= -½.

Step 3: Substitute x into the original formula to find the value of y.

y= (-½)² -½ - 6

=¼ -½ - 6

= -6.25

How many roots does y= 3x^2+2x+6 have?

Your answer should include: None / Zero / 0

What is the turning point of x^2+5x+4?

Your answer should include: -2.5 / 22.75