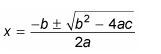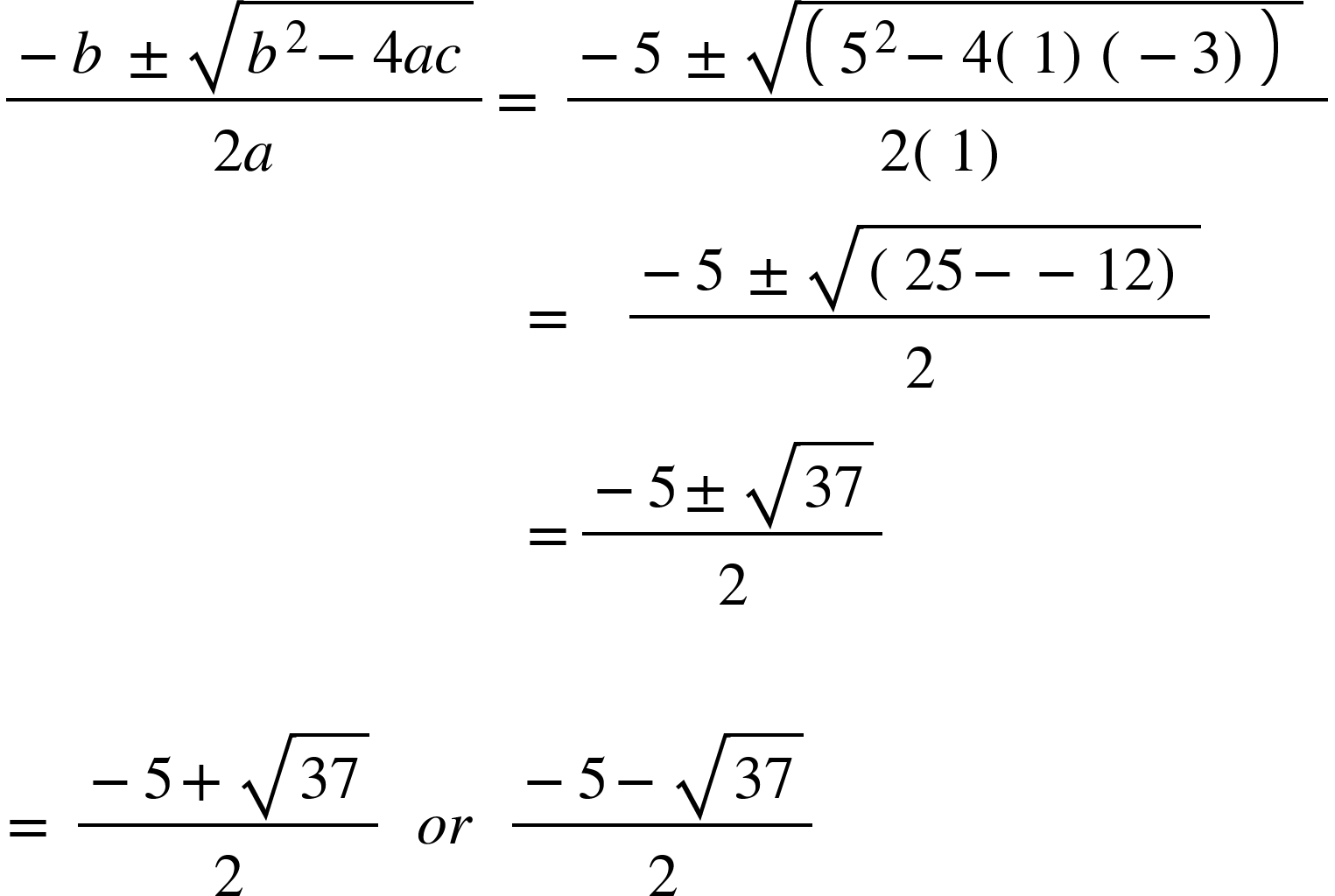Solving Quadratic Equations

Factorise and solve

A quadratic equation is one that has a variable that is squared in it, often an x².

If we look at the graph of a quadratic equation, we can see that it crosses the x axis at two points. This means that quadratic equations can have two values of x when y is zero. We can find these roots by factorising. So here’s my method to factorise quadratics.

Let’s take x² + 2x - 3

Step 1: Look for the factors of the constant, in this case the constant is -3

1 x -3 or 3 x -1

Step 2: Choose the factors that add together to make +2x if they have a coefficient of x.

In this case 3 and -1

Step 3: Divide the coefficient of x into the two numbers above.

x² +3x- x -3 & +3x -x = 2x

Step 4: Split the quadratic so you have two two term expressions to simplify

x² +3x I - x -3

Step 5: Factorise the two expressions

x(x+3) I -1( x+3)

You should see that the brackets have the same expression, in this case (x+3). This means (x+3) is one bracket, the second bracket is formed by joining the terms outside.

x(x+3) -1( x+3)

(x+3)(x-1)

Step 6: Check your answer by expanding the bracket.

(x+3) (x-1) = x² + 2x - 3 so we’re right!

Now that we can factorise quadratics, here’s how we solve them!

When solving quadratics we want to find out what x is equal to when y=0

x² + 2x -3=0

(x+3)(x-1)=0

When we have two things multiplied together that equal 0 that must mean one of them is equal to zero. For example A x B=0 then A could be 0 or B could be 0. When we have our quadratic in a factorised format we can see this clearly.

(x+3) (x-1) = 0

x+3=0 therefore x = -3

x-1=0 therefore x = 1

Using the quadratic formula

When it comes to solving some quadratic equations it is not possible to factorise them. For example: x² + 5x -3=0

In these cases we need to use the quadratic formula. This formula can save your bacon so let’s go over how we use it!

Step 1: Label your quadratic

The abc’s in the formula refer to the coefficients and constants in the quadratic.

ax² + bx + c = 0

x² + 5x -3 = 0 For this example: a=1 b=5 c=-3

Now we need to write out the formula and substitute in the numbers

You will then need to write you answer to the required number of decimal places, or leave it in surd form.

Approximate solutions

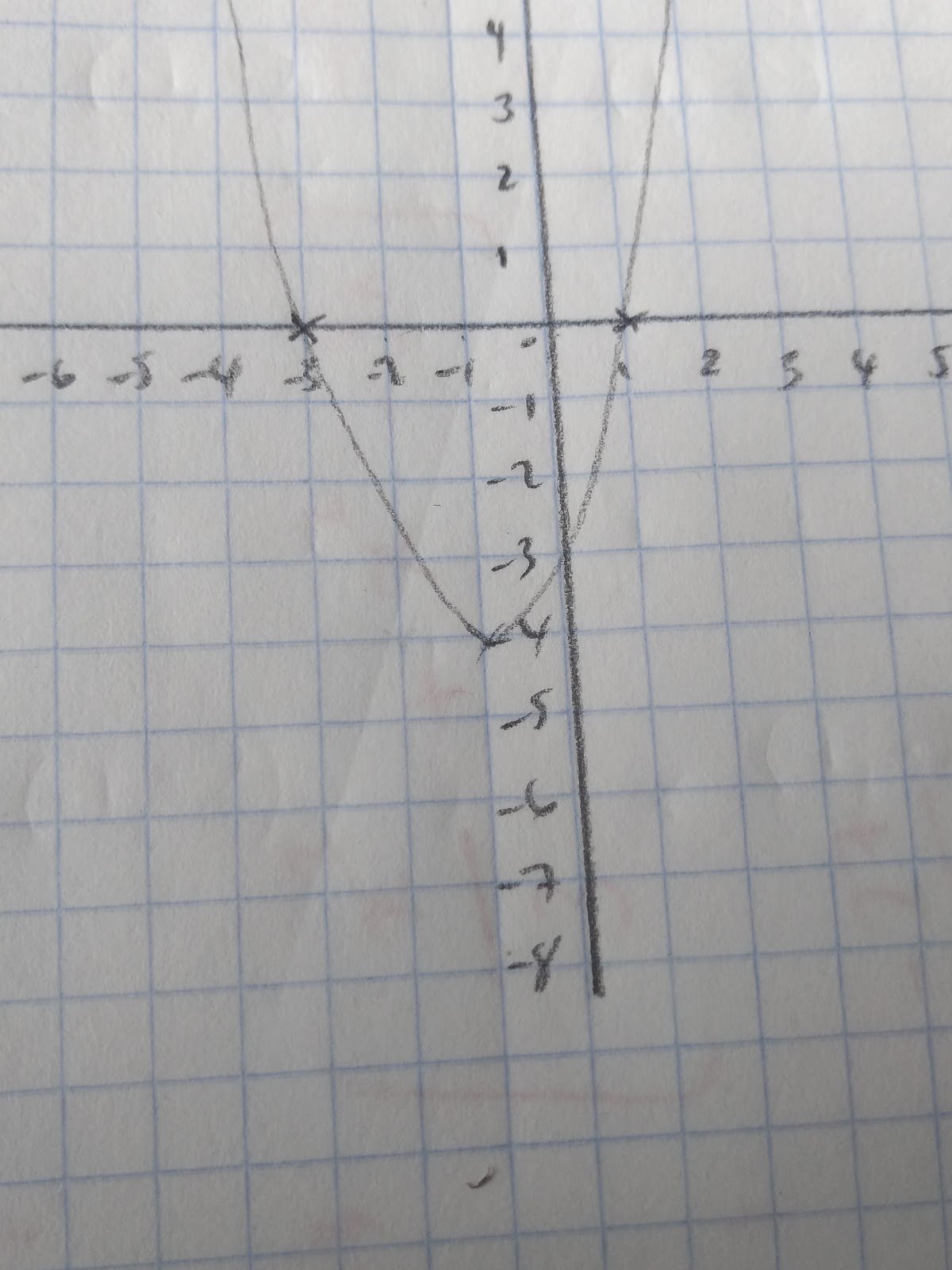
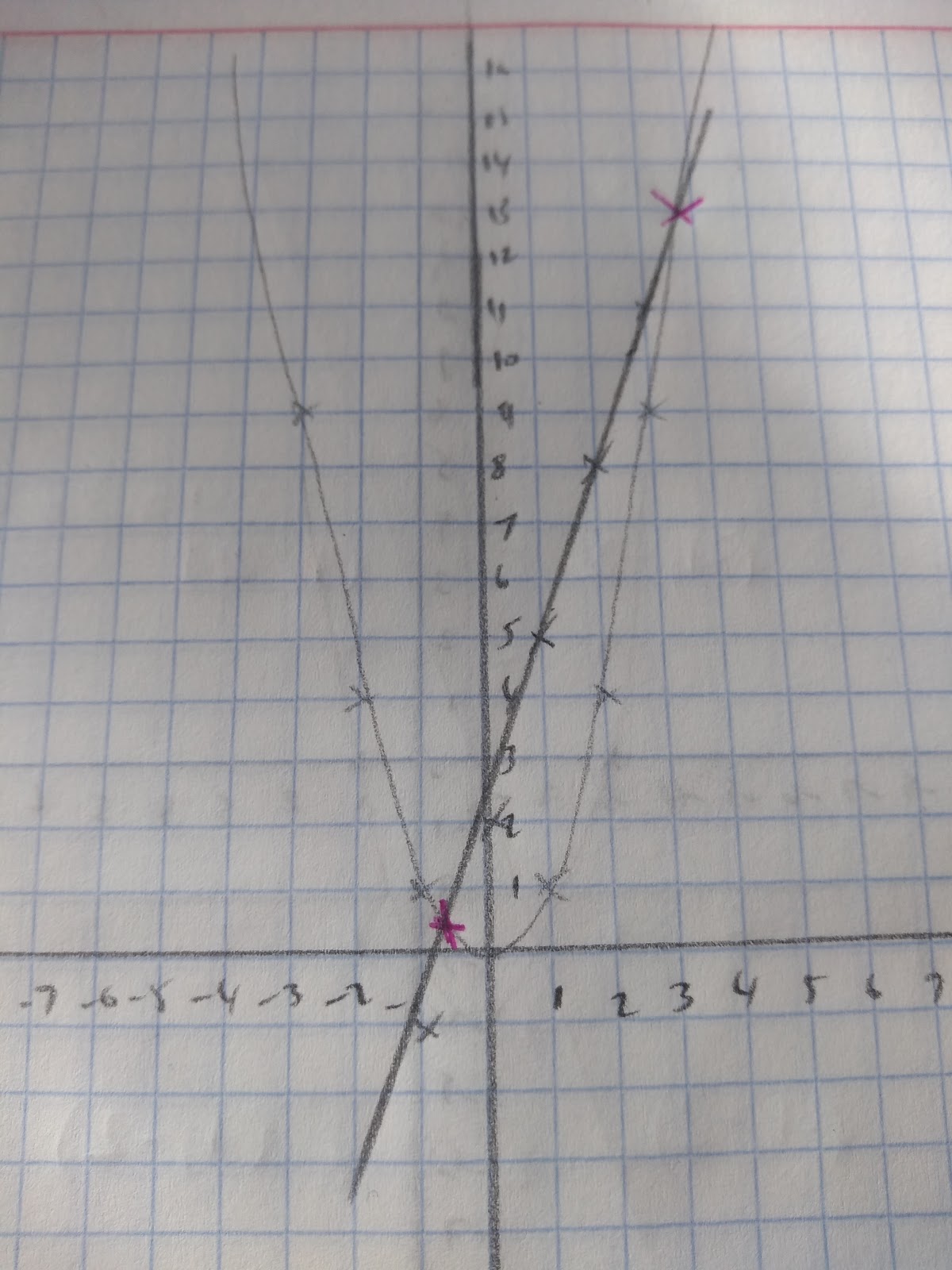
Sometimes we will given a graph of a quadratic and asked to find approximate solutions.

For example, solve the equation x²-3x-2=0 using the graphs given:

The graphs drawn are y=x² and y=3x+2

Our approximate solutions can be read off the graph. This is because if we rearrange our equations we can get:

x²-3x-2=0

x² =3x+2 if we make these both equal to y we can solve them graphically

So the points that cross both graphs are ~(-0.8,0.2) or (3.5,13)

Approximate solutions using iteration

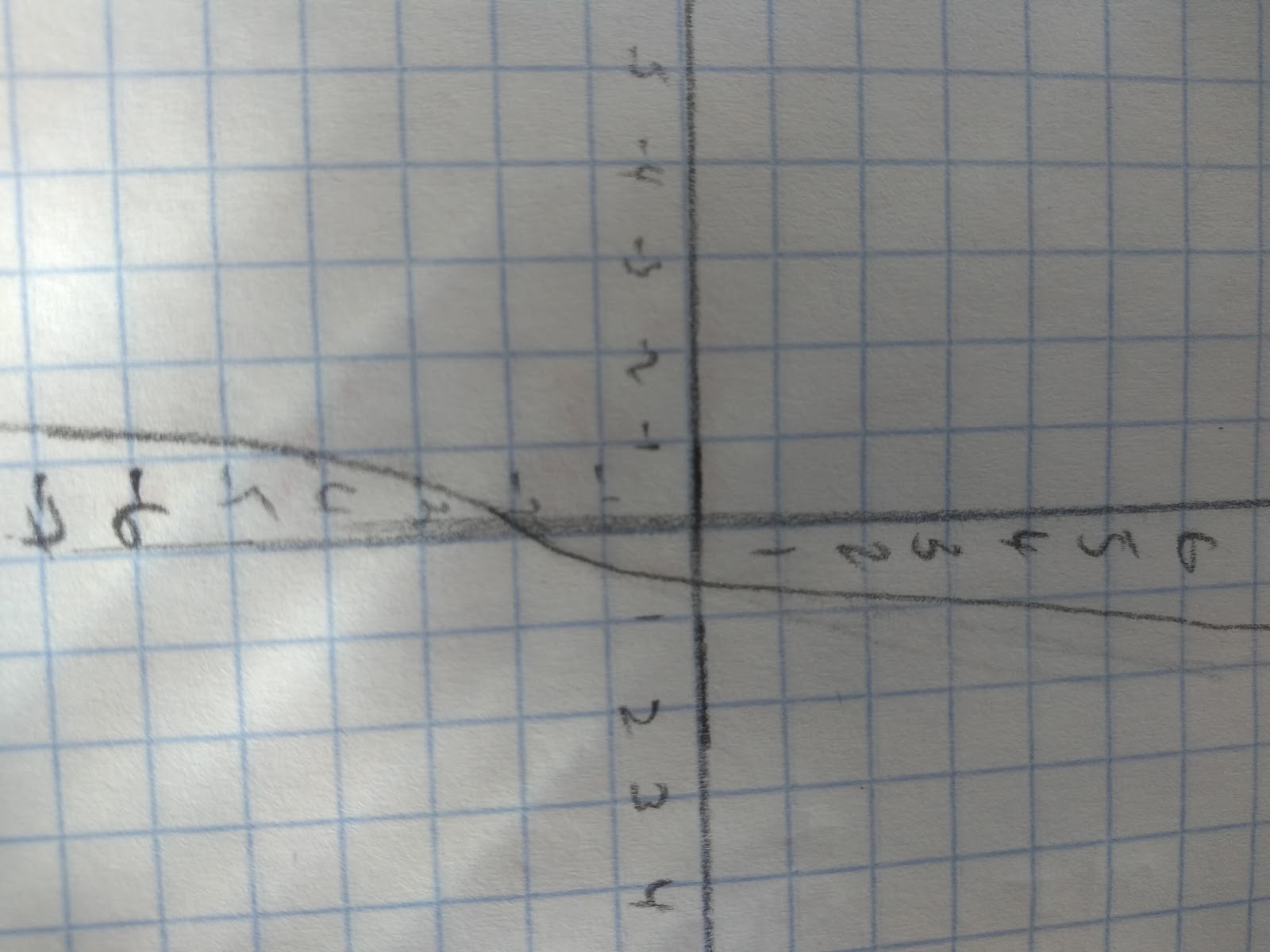
To approximate solutions we can use an iterative process. This involves setting up an equation where you or your calculator uses the answer from the previous calculation. Iteration literally means repetition, so we’re setting up an equation that will repeat a process to find an approximate solution. This is often very useful when finding roots. For example, this graph shows the equations: y = x³ +3x -2.

We can see that there are is a root at approximately x~0.5

By using iteration we can find a more exact approximation of our root. Here’s how we set up an iterative equation. We’ll use the example

Step 1: Rearrange your equation.

For example: 0=x³ +3x-2

The first thing that I want to do is make x the subject of the formula, by rearranging the equation:

0 =x³ +3x-2

2- x³=3x

1/3(2- x³) =x

Step 2: Add subscript to your formula to indicate which processes will be repeated.

Subscript is the small letter and numbers.

x_n refers to your current value of x.

x_n+1 refers to the next term in the iterative process.

Therefore:

1/3 (2- x³) = x will become:

1/3 (2 - xn³)=x_n+1

Step 3: Put in your values.

We have been given initial approximation x~0.5

Now we need to substitute in the values:

x~0.5 x_0= 0.5 This is the value that we will start with

1/3 (2 - xn³ )=x_n+1

1/3 (2 - (0.5)³)=x_n+1

0.625= x_1

Now we use this value as x_1 = 0.625

1/3 (2 - (0.625)³)=x_2

1/3 (2 - (0.625)³)=x_2

0.58528645…. =x_2

You will then need to continue this process until a given point. Make sure that the values are converging, heading towards a similar point. This is important! If they are not then you have probably made an error.

Now this process can be very time consuming which is why you can set up an equation on your calculator.

1. Write the first value given (in the case above 0.5) into your calculator and press ANS
2. Then Put in the equation into your calculator, using ANS in place of x_n
3. Keep pressing = and each answer will be an iteration.

Find the root of y= x^2- 3x +1 to the x^3 to 3 dp.

0.350