Pythagoras' Theorem
Finding the hypotenuse
Fundamental to using Pythagoras’ theorem is finding the hypotenuse. The hypotenuse is ALWAYS:
- The longest side
- Opposite the right angle
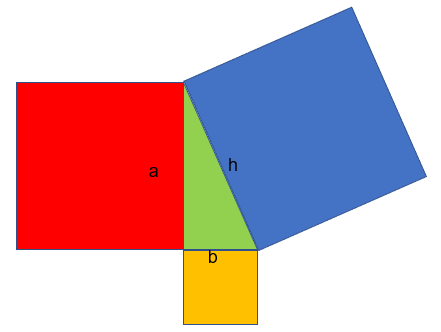
Pythagoras managed to figure out that if you have a right angle triangle and draw squares on the edge of each, the square made from the hypotenuse has the same area as the two other squares put together:
Therefore, if we call our sides a,b and h ( h being our hypotenuse).
Then h2 = a2 + b2
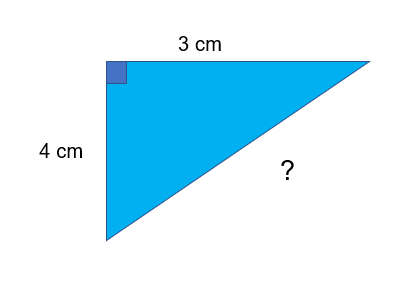
For example:
?2 = a2 + b2
?2 = 32 + 42
?2 = 9 + 16
?2 = 25
? = 5
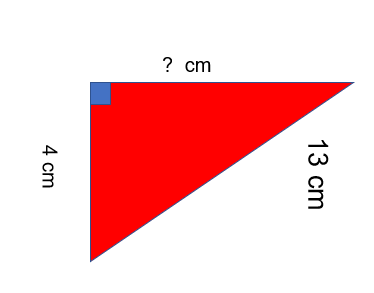
Finding a smaller side
In order to find either one of the smaller sides, we need to rearrange the formula.
Eg. h2 = a2 + b2
These can be rearranged to:
a2 = h2 - b2
b2 = h2 - a2
Always subtract from the hypotenuse.
Eg.
a2 = h2 - b2
?2 = 132 - 42
?2 = 169 - 16
?2 = 153
? = √153 =12.37 (to 2 dp)
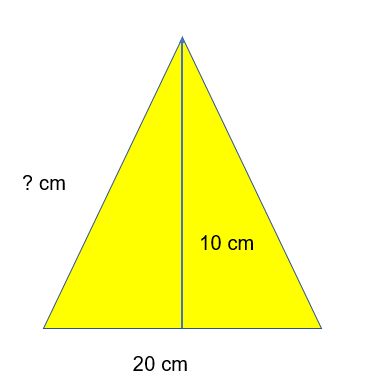
Sometimes you will need to make a right angle triangle by splitting an isosceles triangle eg.
If you divide the bottom line in half you will get two right angle triangles.
The height of these triangles is 10, the base will be 10 and then you just need to find the hypotenuse using our good friend Pythagoras!
?2 = a2 + b2
?2 = 102 + 102
?2 = 200
?= √200 = 14.14 (2 dp)