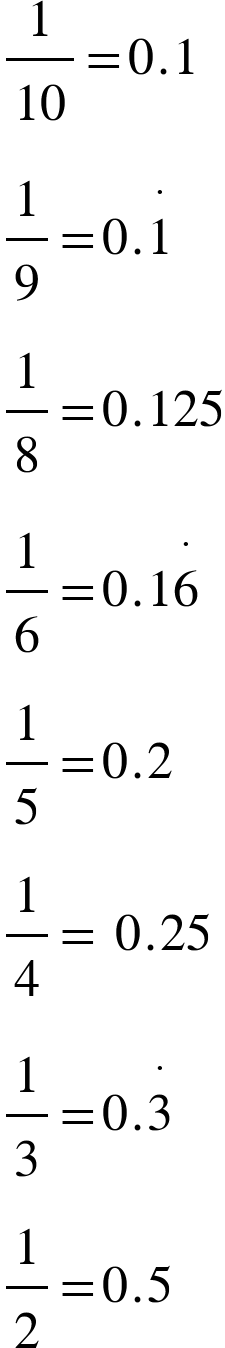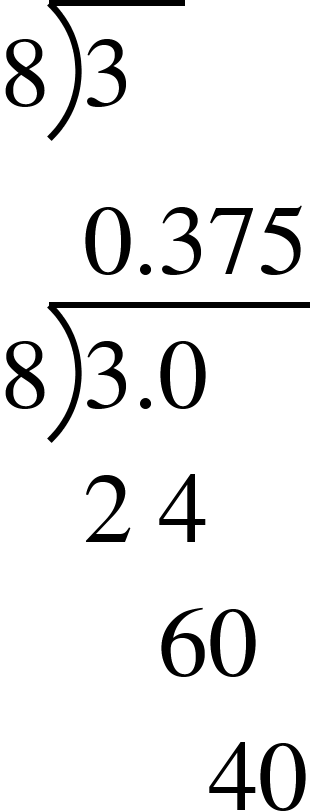Fractions, Decimals and Percentages

Changing Fractions to Decimals

Key fractions/decimals to know:

Changing Fractions to Decimals With a Calculator

To change a fraction to a decimal, just remember to divide! That’s what that line between the numbers means.

Therefore if you want to change 2/5 into a decimal, simply think divide 2:5 = 0.4

Equally, if you are able to learn the key fractions in the table above you will just need to remember that 1/5= 0.2 and then you can double it!

Changing Fractions to Decimals Without a Calculator

If you are tackling the non-calculator paper you will need to use another methods to divide. I would strongly recommend using the ‘bus-stop’ method.

So to turn 3/8 into a decimal without a calculator, remember as before it’s just 3/8 = How many 8s in 3.

Write it as the bus-stop method.

Use long or short division to get your decimal. Here I have used long division.

Recurring Decimals into Fractions

All fractions can be written as decimals, however some fractions are terminating whilst others are recurring.

Terminating fractions are decimals that have a finite number, for example ½ is a terminating fraction as it is written as 0.5.

1/9 however is a recurring decimal, it is written as 0.11111111….. The 1 will carry on forever. Therefore we write it as 0.1, a dot over the one. In some countries they write this with a line instead of a dot but it means the same thing. You only put the dot over the numbers that repeat.

Eg. 0.1212121… would be written as 0.12, with dots over the 1 and the 2

Of the key fractions to remember, 1/6, 1/3, 1/7 are all recurring decimals.

How to do it:

You need to be able to convert recurring decimals into fractions and here’s how.

Let’s take 0.13131313… as an example:

Step 1: Label the recurring fraction t (or any name or letter you like!)

0.131313… = t

Step 2: We want to get one part of the repeating sequence on the left hand side of the decimal point.

In this case we will need to multiply t by 100 to get 13.13131313….

Step 3: Now we can form an equation to find t as a fraction.

100t = 13.1313….. t=0.131313

So if 100t - t = 99t

Then 13.1313… - 0.1313=13

So we can make the equation

99t = 13

t = 13/ 99

You’ve now got a fraction! If you have a calculator check it to make sure it is correct.

Work with Fractions and Percentages

A percentage is a fraction that is out of one hundred. The word cent means 100 (think French!) Therefore to convert fractions to percentages we need to make them equivalent to a fraction out of 100. Alternatively, to turn a fraction into a percentage simply convert it to a decimal (divide the numerator by the denominator) and multiply it by 100.

Eg. 5/8 = 0.625 multiplied by 100 = 62.5%

A key point to remember is 100% = 1

Therefore 150% = 150/100 = 1.5

Fractions and Ratios

Fractions allow us to compare things against one whole. Whilst ratios show the relation between things. Therefore you need to be careful when dealing with fraction and ratio questions. Eg. Thirty out of seventy school children take the bus to school, all the others walk.

What fraction of the school children walk?

This question is asking for a fraction, therefore we need to think about how many children there are altogether as this will be the denominator, the number of children that walk to school will be the numerator: 30/70 = 3/7.

What is the ratio of children who take the bus to school to children who walk to school.

This question is asking for a ratio, for us to compare the parts.

30:40

30 children take the bus : 40 children walk

In total 30+40= 70 which is all of our children.

This ratio can simplify down to 3:4

What is 3/5 as a decimal?

0.6

⅖ of children prefer Bubble Gum to Chewing Gum. What is this as a ratio?

2:3