The Number System and Types of Numbers

Ordering Numbers

Symbols to order numbers:

X > Y, X is greater than Y

X ≥ Y, X is greater than or equal to Y

X < Y, X is less than Y

X ≤ Y, X is less than or equal to Y

X=Y, X is equal to Y

X≠Y, X is not equal to Y

Eg. 10 > 3, 6 ≠ 5…Think of the crocodile’s mouth! less < more!

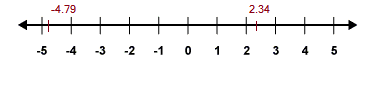
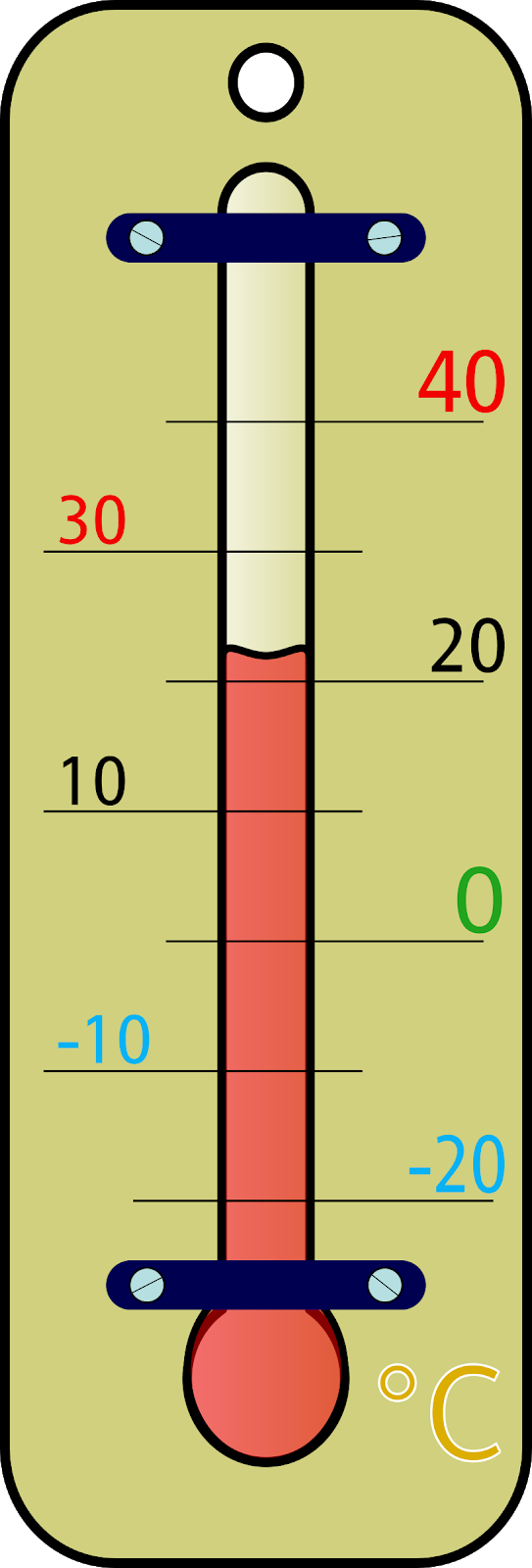
Negative and Positive Numbers

To order negative and positive numbers use a number line to help you. Anything to the left of 0 will be a negative number. Think about temperature, anything below zero will be freezing, so it will be a negative number.

Eg. -2 < 0.5

Ordering Decimal Numbers

When ordering decimal numbers it is important to look carefully at the numbers in relation to the decimal point. Line the numbers up to compare them. Compare the numbers to the left first.

I.e. 12.5623, 12.5__7__09

12.5709 is bigger because 7 is bigger than 6.

Place Value

The place value of a digit tells you how much that number is worth. For example in 6532: We can use our knowledge of place value to work out calculations.

I.e. If 25 x 98 = 2450

Then 2.5 x 98= 245 We know this because 25 is 10 times bigger than 2.5

Then 2.5 x 9.8= 24.5

We know this because 25 is 10 times bigger than 2.5 and 98 is 10 times bigger than 9.8, therefore our answer is going to be 100 times smaller (10 x 10= 100)

This can also be used with calculations that involve division.

I.e. If 2450 / 98 =25

245 / 98 = 2.5 As there will be 10 times fewer 98s in 245.

Types of Numbers

There are lots of different types of numbers. Here are the key types of numbers that you need to know:

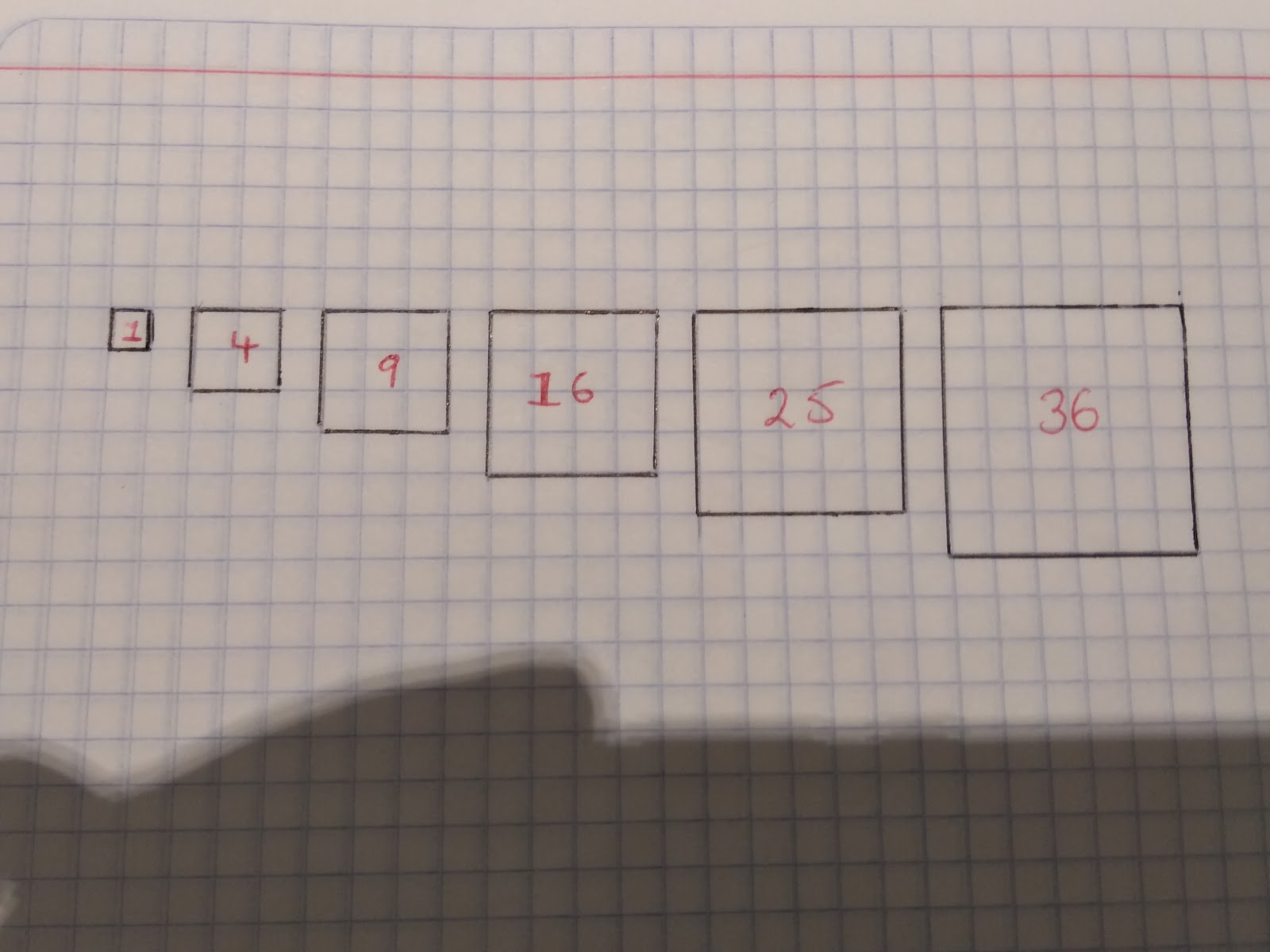
Square Numbers

These numbers are numbers multiplied by themselves. Because a negative number multiplied by a negative number results in a positive number, square numbers will always be positive when they are squared.

1x1 = 1², 2x2= 2², 3x3= 3², 4x4= 4², 5x5= 5², 6x6 = 6²

Cube Numbers

Cube numbers are numbers multiplied by themselves 3 times.

Eg. 1 x 1 x 1=1³=1

2 x 2 x 2 = 2³ = 8

3 x 3 x 3 = 3³ = 27

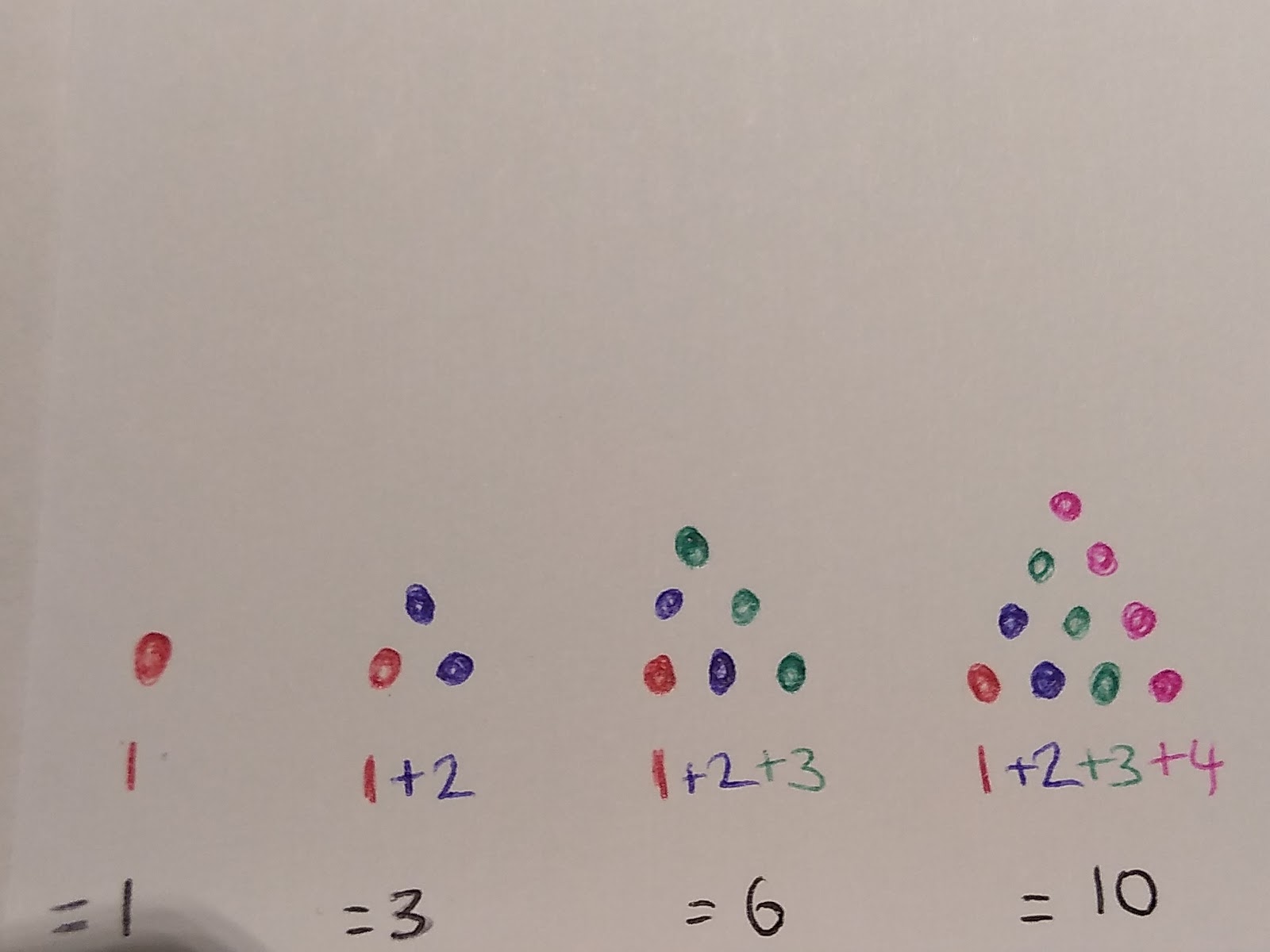
Triangular Numbers

These numbers are made from adding the next number in the sequence with the original numbers.

Prime Numbers

Prime numbers are numbers that only have two factors: 1 and themselves.

Therefore 1 is NOT a prime number as it only has 1 factor: 1.

The only even prime number is 2.

Key prime numbers to learn off by heart:

2,3,5,7,11,13,17,19….

Key definitions to learn:

Factors: Integers (whole numbers) that multiply together to make other numbers. They are also known as divisors. E.g. The factors of 8 are: 1,8,2,4

Because:

1 x 8 = 8

2 x 4 = 8

__Common factors: __factors that two numbers both have. The best way to find a common factor of a small number is to work out the factors of both numbers and then select the numbers that are in both lists.

To find the Highest Common Factor (HCF), select the highest number in both lists.

Eg. The common factors of 6 and 8:

Factors of 6= 1, 6, 2, 3

Factors of 8= 1,8,2,4

Common factors of 6 and 8 = 1 and 2

The Highest Common Factor= 2 as this is the highest number in both lists.

Multiples: Multiples are the result of a multiplication

Eg. The first four multiples of 6 are: 6,12,18,24….

Common multiples: The multiples that two numbers have in common.

You may be asked to find the lowest common multiple or this may be useful when solving problems.

Eg. Common multiples of 8 and 6

Multiples of 8 = 8,16,24

Multiples of 6 = 6,12,18,24

The lowest common multiple is 24

Prime Factorisation

This is important as the Unique Factorisation Theorem states that every number is a prime number itself or can be written as a product of its primes.

This is when we write it out as the number that is the answer to a calculation where prime numbers have been multiplied together.

To do this we need to remember our prime numbers and think about which prime numbers will divide into a given number.

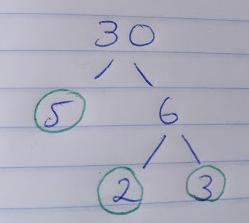
Eg. Write 30 as a product of its primes:

Prime numbers that will help us: 2,3,5,7,11,13

Ask yourself which numbers will go into 30- you could choose 2,3, or 5 from the list above.

Choose whichever prime number you want.

I’m going to choose 5 so I circle the 5 and move onto find the prime factors of 6, 2 and 3 are prime factors of 6 so I circle them and have nothing left to factorise!

This leaves me with my final answer that 30=2x3x5

In this second example I can write my answer in two ways, 90= 2x3x3x5 or 90=2x32 x5

This 90=2x 32 x5 is my answer written in index form as I have used indices.

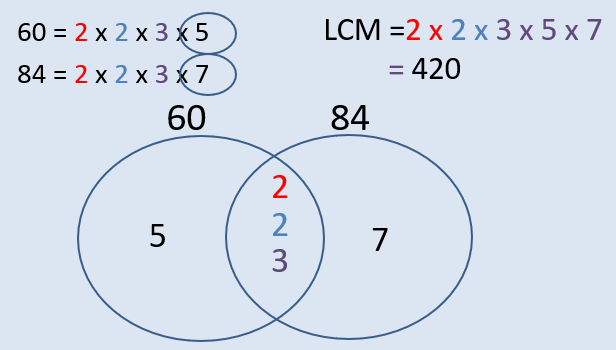
Using Venn diagrams to work out HCF and LCM

Now we know how to write numbers as a product of their prime factors we can use this to work out the highest common factor (HCF) and lowest common multiple (LCM).

Given that we can write every number as a product of its prime factors, writing numbers in this format allows us to see the difference between the numbers in terms of their prime factors.

So, how does it work?

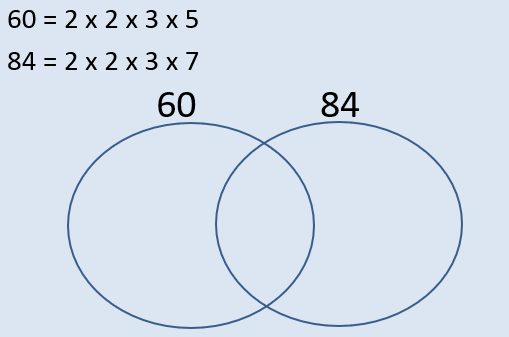
Step 1: Write each number as a product of its prime factors

Step 2: Draw two, overlapping Venn diagrams

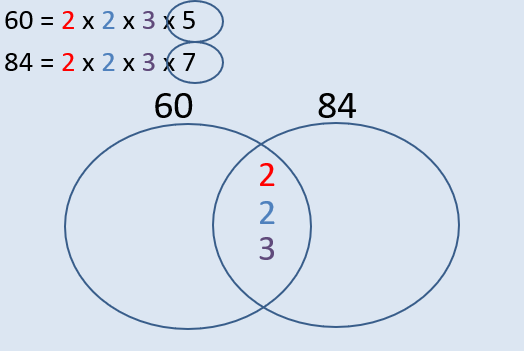
Step 3: Place any of the numbers that are in both numbers’ prime factor decomposition in the overlap

Step 4: Place any other number in its corresponding circle

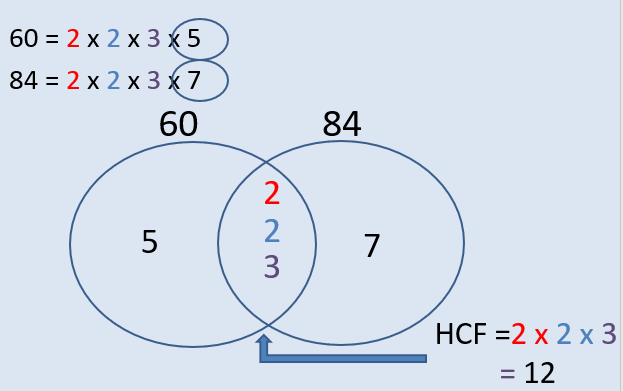
Step 5: To find the Highest Common Factor (HCF)multiply the numbers in the overlap of the Venn diagram together

Step 6: To find the Lowest Common Multiple (LCM) multiply all the numbers in the Venn diagram together.

E.g Find the HCF and LCM of 60 and 84

Listing Systematically

Listing combinations of things in a systematic way is a key skill. You can use any method you like, but I would strongly recommend using lists, tables or diagrams to show your working and clearly show your answer.

Eg. Jen and Berry sell ice cream, you can choose to have vanilla, chocolate or strawberry in either a cone or a cup.

How many different types of ice cream can they sell?

Table

List method:

Cone Vanilla

Cone Chocolate

Cone Strawberry

Cup Vanilla

Cup Chocolate

Cup Strawberry

Diagrams:

Using the Product Rule when Counting

In foundation this type of question can be solved by using the above methods. However on the Higher paper you need to know the Product Rule for Counting.

This rule states that if there are a certain number of ways of doing a task T and there are Y ways of doing another task, the total number of ways a task can be done is T x Y. It helps us work out the number of options we have.

Eg. Jill has 4 playing cards, Sasha has 10 different playing cards and Pete has 6 cards. How many different combinations of cards can they have?

4 x 10 x 6= =240

Using the fact that 46 x 85 = 3910 what is 391/46 = ?

8.5

Write down the highest common factor and lowest common multiple of 60 and 84.

Your answer should include: 12 / 420

Harry has a padlock with 3 sections, each has the options 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. How many different combinations would he need to try to open the padlock if he had forgotten the code?

1000
Explanation: Each padlock section has 10 possible options, so combined that's 10 x 10 x 10, or 1000.