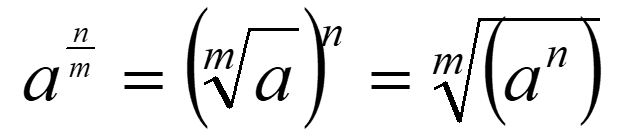Indices
Powers and Roots
Powers and roots- the ‘o’ in bodmas or ‘i’ in bidmas part of any calculation. Powers tell you how many times you multiply a number by itself, whilst roots tell you the opposite. Powers are also known as indices.
You need to be able to use roots and powers and also recognise the following powers: 2,3,4,5 Eg.
Learning these by heart will help you a lot!
Estimating the Answer to Powers and Roots
If you have learnt the above roots and powers, estimating powers and roots will be a lot easier! We will need to know which roots or powers will be between the one that we have been asked to identify.
Example 1
Estimate the 3__√__18. In this case we need to remember some of our cube roots.
If we have learnt the roots above, we will know that 3√__8 = 2 and 3√__27 = 3, therefore our answer must lie somewhere between 2 and 3, so a good estimate would be 2.5.
Example 2
Estimate the root of __√__130
If we think about our square numbers, __√__121 = 11, __√__144 = 12
Therefore an estimate of this root would be 11.5
Remember n1/2 = __√__n
Therefore if you’re asked to estimate a number to the power of a to the power of 1/2 that’s the same as square rooting.
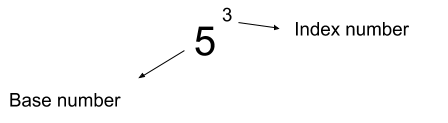
Indices
Above is an example of a number written in index form. The index number tells us how many times we multiply the base number by itself.
This means 53 = 5 x 5 x 5
The plural of index is indices and these number are sometimes referred to as indices, powers or exponents.There are several key rules to learn for simplifying and using indices.
Multiplying indices: ____an__ x a__m__ =a__n+m
Example: If we know 53 = 5 x 5 x 5 and 54 = 5 x 5 x 5 x 5
Then,
= 53 x 54
= 5 x 5 x 5 x 5 x 5 x 5 x 5
OR
= 57
Dividing indices:__ a__n__ / a__m__ =a__n-m
Example:
If we know 95 = 9 x 9 x 9 x 9 x 9 and 92 = 9x9
Then
= 95 ÷ 92
= 9 x 9 x 9 x 9 x 9 / 9 x 9
= 9 x 9 x 9
Or
= 93
Be careful with these questions, remember you can have negative indices eg.
= 95 ÷__ __9-2 (Remember 5 - -2 = 7!)
= 97
Indices with brackets: __(an)__m__ = (a)__n x m
Example:
(42)3 = 42 x 42 x 42
= 4 x 4 x 4 x4 x 4 x 4
= 46
Trickier brackets: __(ab)m = (a)__mx __(b)__m
Example:
(5b)4
=54 b4
=625b4
a1=a
Anything to the power of 1 is itself. Technically every number should be written with an index of 1.
Examples:
81=8
0.5621=0.562
5½1=5½
a0=1
Every single number to the power of 0 = 1. EVERY number, negative, positive, fraction, decimal.. It will always equal 1!
Example: 510317.3170=1
Fractional and Negative Indices
The base number of an indice can be any sort of number, and equally when we can have negative and fractional indices.
Negative indices:
Fractional Indices:
More complicated fractions:
Example:
82/3 = (3√8)2
This works because if you think of the multiplication of indices:
81/3 x 81/3 = 82/3
Standardform
We use standard form to write very large numbers or very small numbers. It is also known as standard index form or scientific notation.
Writing numbers in standard index for:
A number is only in standard form if it follows this rule:
When: 1 < = A < 10 and a number is written as: A x 10n
It can be 1 or any number up to 10 but it cannot be 10 !
The n can be any whole number (integer)
To write really big numbers such as 5,400,000 think about the digits that would make a number less than 10. Then think about how many times you would need to multiply that number by 10.
In this case 5.4 would be the number that’s one or more but less than 10.
5.4 x ? = 5,400,000
5.4 x 1,000,000 = 5,400,000
5.4 x 106 = 5,400,000
For super small numbers we need to divide by 10 or multiply by 10^-n t
Example:
0.0001756 remembering that our digits need to fit.
When 1 <= A < 10 = A x 10n
So
=1.756 x 0.0001=0.0001756
=1.756 x 10-4
Writing numbers as ordinary numbers
You also need to be able to write numbers in standard form as ordinator numbers:
For large numbers, remember that for every power of 10 you move all the digits one place to the left of the decimal place. Eg.
5.6 x 10 = 56
5.6 x 102 = 560
5.6 x 103 = 5600
5.6 x 104 = 56000
5.6 x 105 = 560000
For very small numbers, remember that for every negative power of 10 you move the digits one place to the right of the decimal place.
5.6 x 10-1 = 0.56
5.6 x 10-2 = 0.056
5.6 x 10-3 = 0.0056
5.6 x 10-4 = 0.00056
5.6 x 10-5 = 0.000056
Multiplying and dividing in standard index form
You may be asked to multiply two numbers in standard index form, and then to give you answer in standard index form.
Here’s the steps with an example along the way to show you how to multiply
= 4.2 x 102 x 2.2 x 105
Step 1: Rewrite the equation so that your index parts are together and your non-index parts are also together.
=4.2 x 102 x 6.2 x 105
=4.2 x 6.2 x 105 x 102
Step 2: Multiply the non index numbers together
=4.2 x 6.2 x 105 x 102
=26.04 x 105 x 102
Step 3: Check and make sure all your numbers are in line with the standard index form rules. In this case they are not, so we need to put 26.04 into standard index form:
26.04= 2.604 x 10
Now we can rewrite the equation as:
= 2.604 x 10 x 105 x 102
Step 4: Multiply the indices and write your answer in standard index form
=2.604 x 108
Adding and subtracting in standard index form
With indices you can only ever add them together if they are the same.
Therefore, when it comes to adding and subtracting in standard index form you need the ‘index of 10’ to be the same for each number.
Eg.
1.56 x 105 + 2.56 x 104
Step 1: Make both numbers have the same power of 10
= 1.56 x 105 + 2.56 x 104
= 15.6 x 104 + 2.56 x 104
Increase 1.56 by x 10
Then you can divide 105 by 10
If you find this tricky, write out both numbers as ordinary numbers and then see how you can make them equivalent to the same power of 10.
Step 2: Add the two numbers that are not index numbers
=15.6 x 104 + 2.56 x 104
=(15.6 + 2.56) x 104
= 18.16 x 104
Step 3: Check and make sure your answer is in standard index form
= 18.16 x 104
= 1.816 x 105
Follow the same steps, but subtract instead of adding for subtraction questions.