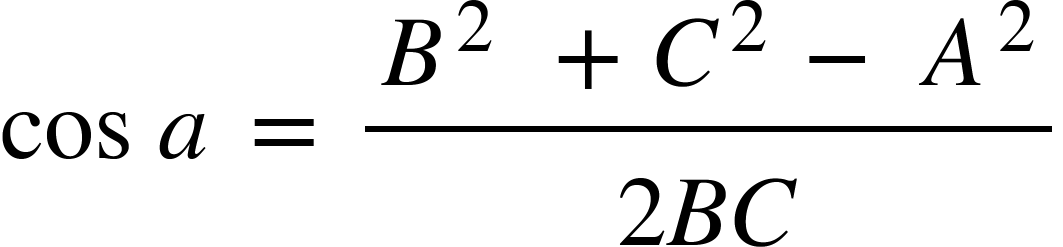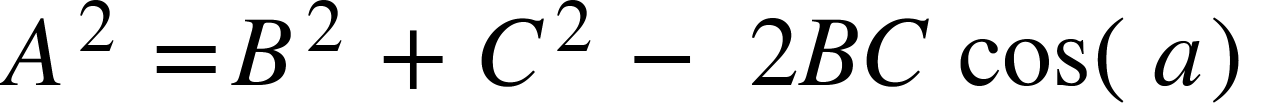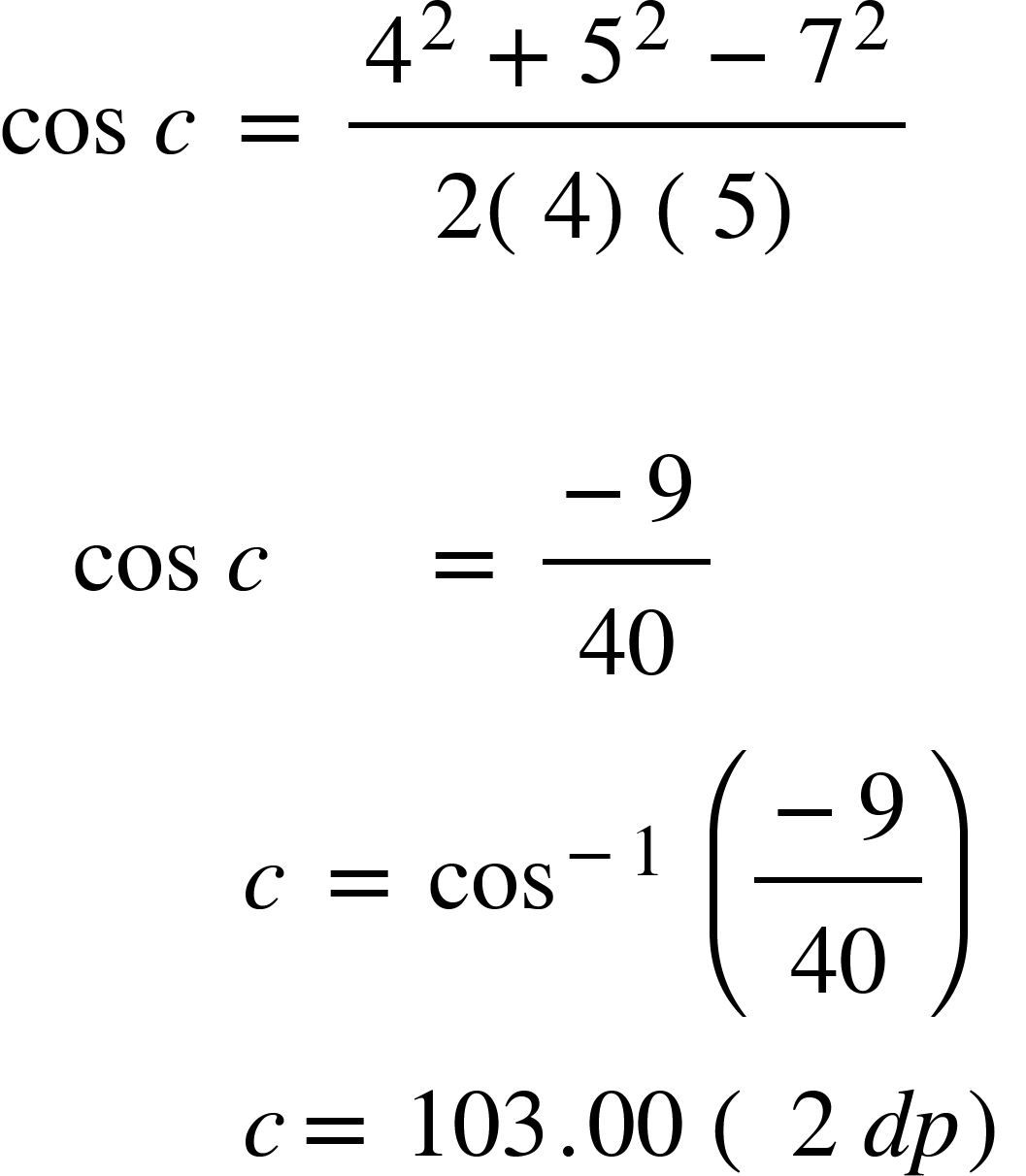Trigonometry

The trigonomic ratios

When it comes to trigonometry there are some key parts that we need to learn. There are many methods, here’s a couple that might help!

SOHCAHTOA - This acronym is used to help you remember the trigonometric ratios.

Which are:

Sine of an angle =Opposite/Hypotenuse

Cosine of an angle = Adjacent/Hypotenuse

Tangent of an angle = Opposite/Adjacent

You need to remember these ratios in order to make sure you choose the right one to solve problems.

A few of my favourite ways to remember these are:

S__ome __O__ld __H__orses __C__an __A__lways __H__ear __T__heir __O__wners A__pproach

__S__ome __O__f __H__er __C__hildren __A__lways __H__ope __T__o __O__wn __A__pples

S__ome __O__ld __H__ippies __C__ome __A__lways __H__elping T__o __O__rder __A__nts

Use a song, use a mnemonic, use whatever you need but make sure you REMEMBER THESE ratios!

Labelling triangle recap

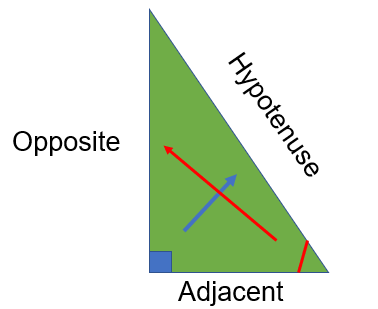
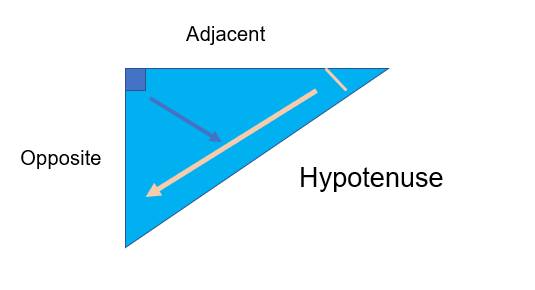
When we looked at Pythagoras we focused on identifying the Hypotenuse which is ALWAYS opposite the right angle. When we use trigonometry we will be either looking for an angle OR a side of a right angle triangle.

Therefore, in trigonometry we need to identify the other two triangles as well. These are the

Adjacent __and the Opposite.__

The Adjacent is adjacent to the angle whilst the Opposite is opposite the angle.

Here’s a diagram to show you what I mean:

Finding Angles

If you have two lengths of a right angle triangle using the trigonometric ratios you can work out the degree of the angles. Depending on the sides of the triangle you will use a different trigonometric ratio, however the process is similar for both of them:

1. Step 1: Label your triangle
2. Step 2: Select your ratio
3. Step 3: Divide the sides
4. Step 4: Inverse the sine, cosine or tan function to find your angle (sin^-1 or cos^-1 or tan^-1)

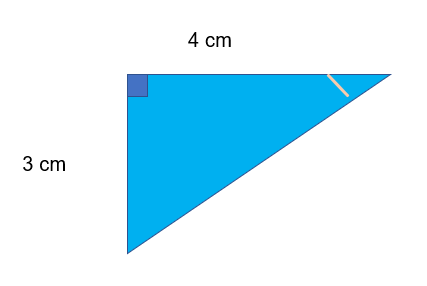
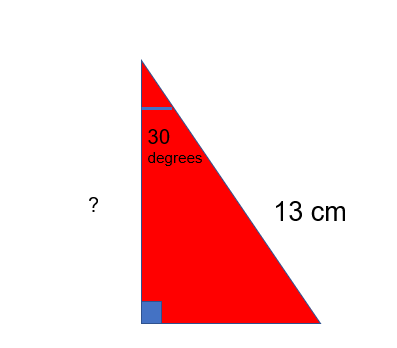
Eg. Find the angle marked in this triangle:

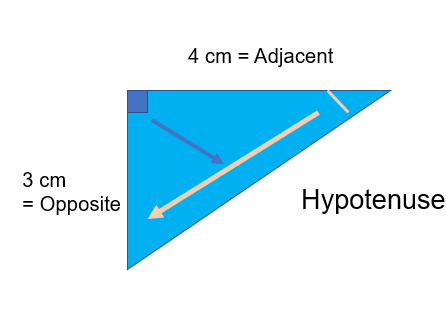
Step 1: Label your triangle

Step 2: Choose your ratio. If we look at our labelled triangle we can see that we have not got any information about the Hypotenuse, but we DO have information about the adjacent and opposite.

Therefore we want to choose a ratio that involves the Opposite and the Adjacent

SOH CAH TOA

In this case it must be the tan ratio

Tan of the angle =Opposite/Adjacent

Step 3: Tan of the angle =3/4

Step 4: Inverse the trigonometric function - on your calculator this will be a button that looks like tan-1

Inverse tan (3/4) = Tan-1 (3/4) = 36.869897645844 or 36.87 to 2 dp

It is REALLY important that you have your calculator in the correct setting. Make sure it is in the DEGREES setting or DEG.

Finding Lengths

To find the length of a trigonometric ratio we have a similar process:

1. Step 1: Label the triangle
2. Step 2: Select the ratio
3. Step 3: Calculate
4. Step 4: Check your answer!

Step 1:

Step 2:

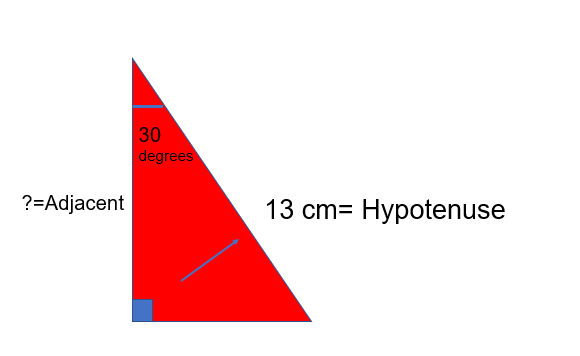
In this case the two values that we have or are looking for are the hypotenuse and the adjacent.

SOH C__AH__ TOA Therefore we will use the Cosine ratio

Step 3:

Cos of the angle =Adjacent/Hypotenuse

We can rearrange this equation to get:

Cos of the angle x Hypotenuse = Adjacent

(Cos (30)) x 13 = 11.26 (to 2 dp)

Step 4:

11.26 cm sounds right and would make a realistic triangle! (It it was 123542 I’d definitely double check!)

Take care to multiply Cos30 by 13 and not Cos (30 x 13) or you will get the incorrect value!

Trigonometry in real life

When it comes to the higher paper, you may often find questions that are wordy and require trigonometry.

For these questions make sure you sketch it out! Draw the description, create a triangle, label and solve.

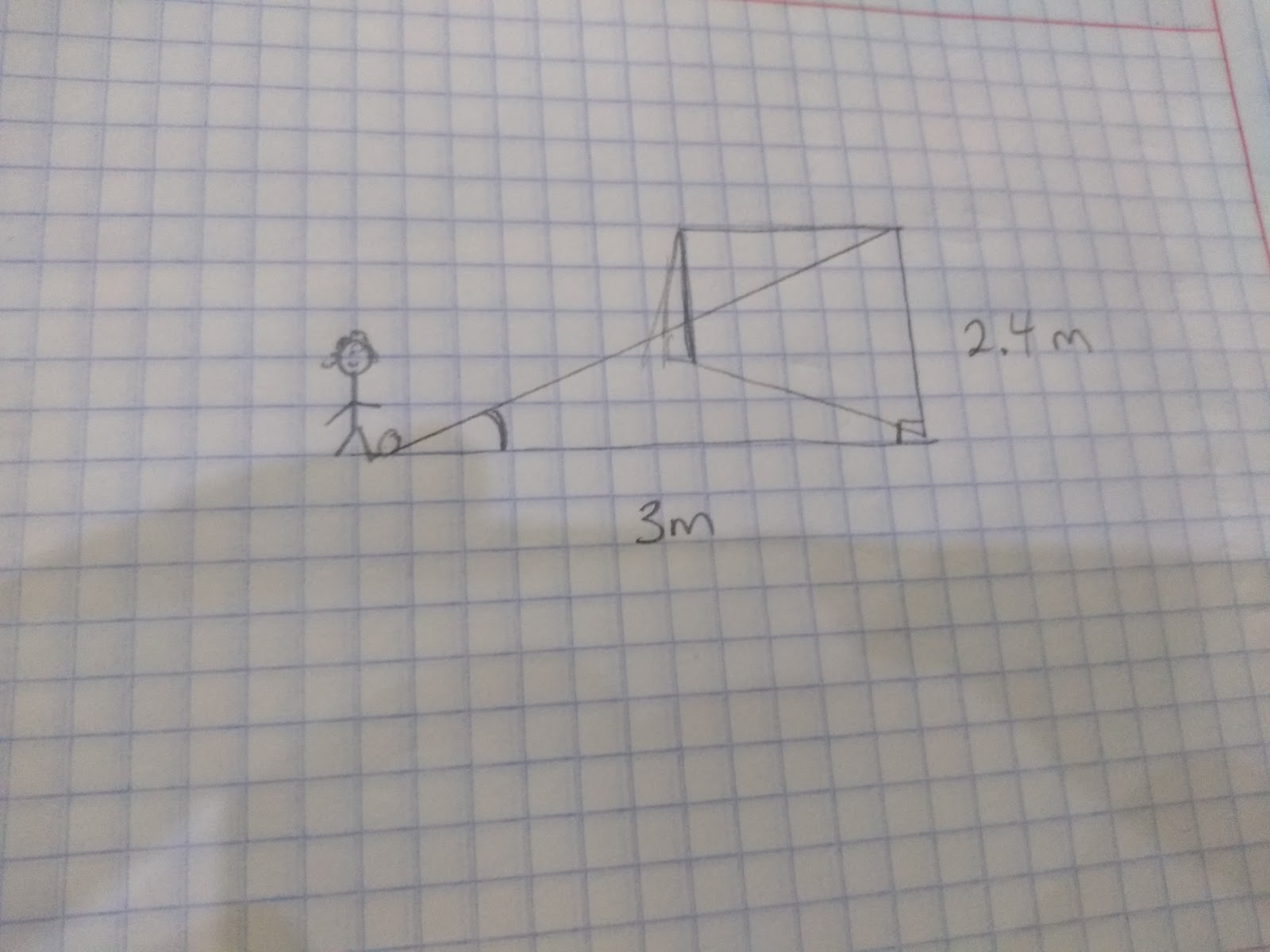
Eg. Katie kicks a football towards a goal. The goal is 2.4 m from the ground and Katie is standing 3 metres away from the goal. If she wants to hit the bar what will be the angle of elevation?

Step 1:

Sketch out the problem

Step 2:

Label the sides, in this case we have information about the Opposite and the Adjacent side, therefore if we check SOH CAH TOA, we will want to find the inverse of the tangent of the angle

Step 3:

Tan Angle = Opposite/Adjacent

Angle = Tan^-1 2.4/3 = 38.67 (to 2 dp)

Katie may want to miss the bar and score, in which case she will need to kick at an angle of just less than 38.67!!

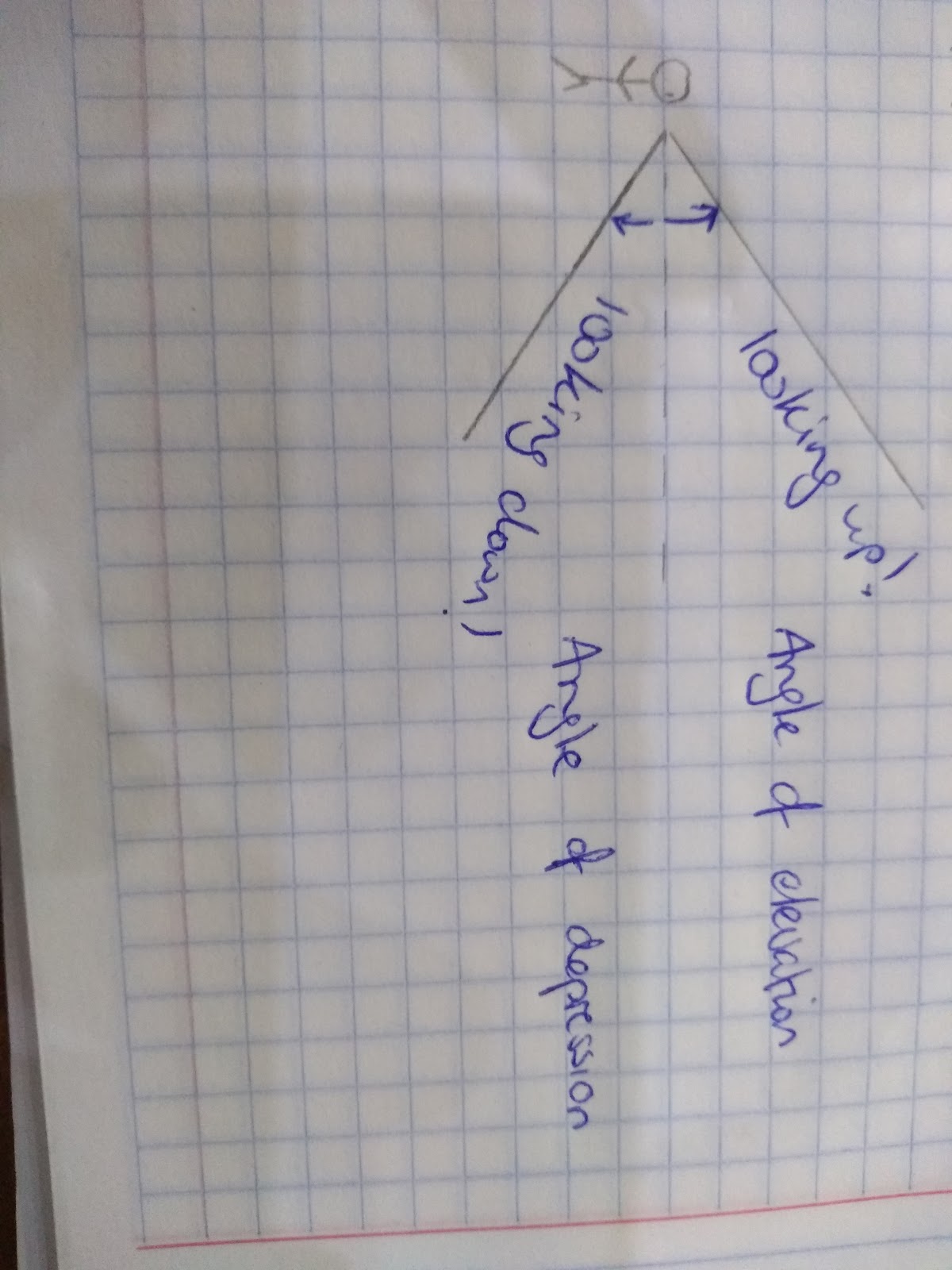
This question referred to an angle of elevation, that’s the angle that goes from the base upwards.

You may also be asked to find an angle of depression that goes from a high point downwards.

Trigonometry in 3D

We may also have to use trigonometry to solve problems involving 3D shapes.

For example:

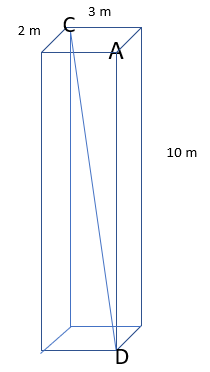
Find the angle CDA

Firstly we need to identify a right angle triangle connected to CD.

We can do this by creating a base from the diagonal of the rectangle on the bottom of the prism.

We then have the hypotenuse that is CD and the remaining side will be 10m.

To work out the base we can use Pythagoras!

Diagonal² = 2² + 3²

Diagonal² = 4 + 9

Diagonal² = 13

Diagonal = Diagonal = √13 (I’m going to leave this as a surd to ensure my working is as accurate as possible)

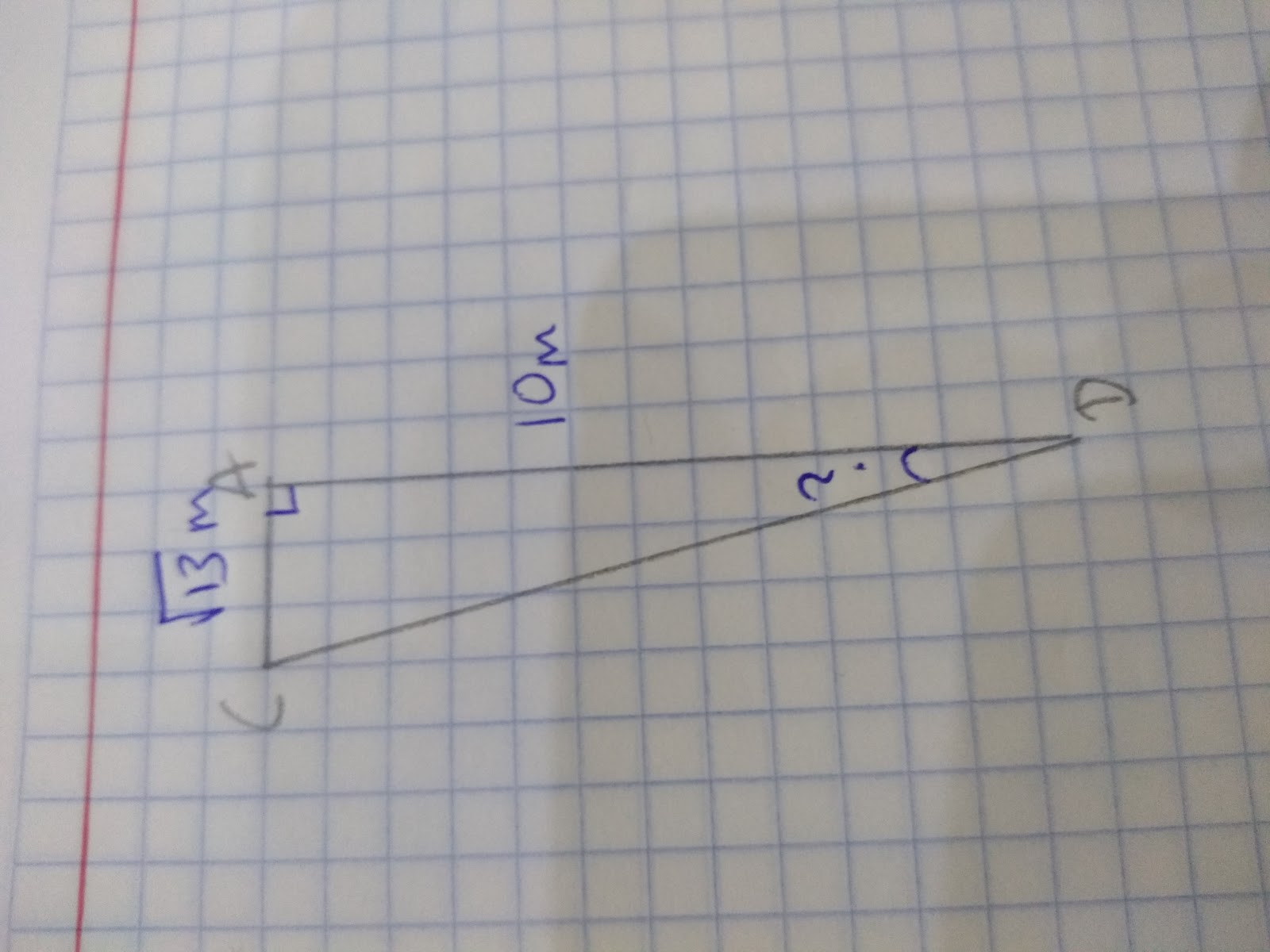
Now we have two lengths we can use our trigonometric ratios to work out the angle. Once again sketch out the triangle to help you:

After labelling the triangles we should see that we have information about the opposite and the adjacent. Therefore we want to use the Tangent ratio.

Tan Angle = √13/10

Angle = Tan^-1 √13/10 = 19.83 to 2 dp.

Key values to memorise

You will also be expected to memorise specific trigonometric ratios:

x	Sin x	Cos x	Tan x
0	0	1	0
30	1/2 or 0.5	√3/2	1/√3 or √3/3
45	√2/2 or 1/√2	√2/2 or 1/√2	1
60	√3/2	1/2	√3
90	1	0	N/A

Learn this table!!! You technically can work these values out using Pythagoras however in the exam you won’t have time so LEARN THEM!!!

Sine Rule

We can also use our trigonometric functions (sin, cos and tan) to work out the lengths and angles of triangles that don’t have right angles!!!

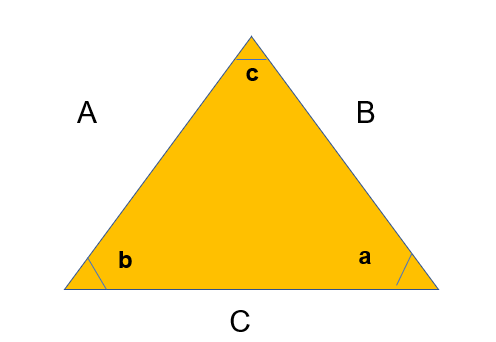
We can use the sine rule, which refers to the following angles and sides:

Sin a / A = Sin b / B = Sin c / C or A / Sin a = B / Sin b = C / Sin c

For example:

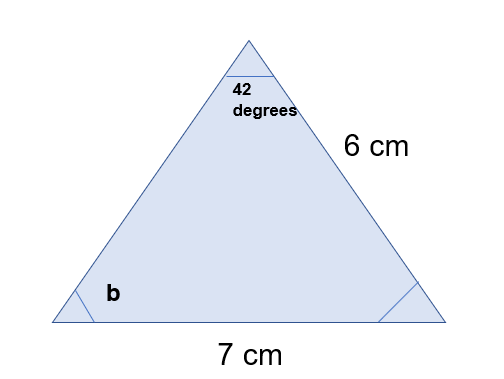
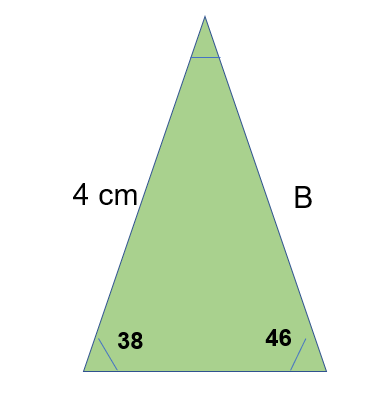
What is the angle b?

To work out be I can use the sine rule as I know:

Sin a / A = Sin b / B = Sin c / C

Therefore:

Sin b / 6 = Sin 42 / 7

To get sin b I just need to multiply by 6 and find the inverse of sine.

Sin b = sin 42 / 7 x 6

b= sin^-1 (sin 42/7 x 6)

b = 35.00 (to 2 dp)

We can also use the other equation to work out lengths.

Eg.

4 / Sin 38 = B / Sin 46

Therefore if we multiply both sides by sin 46 we’ll find B

4 /Sin 38 x Sin 46 = B

4.67 = B

Cosine Rule

We can also use the cosine rule to find angles and sides.

To find angles:

To find lengths:

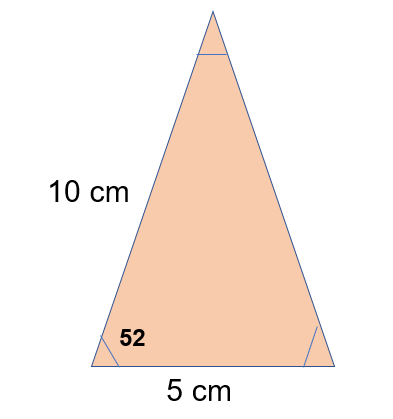
For example, calculate the missing length of this triangle:

Think carefully about how the values given will fit the formula.

The (a) stands for the missing angle, B and C are interchangable.

?² = 5² + 7² - 2(5)(7) cos(52)

?² = 25 +49 - 70cos52

?² = 30.9036…

? = 5.56

We can also use the cosine rule to work out a missing length when given three sides:

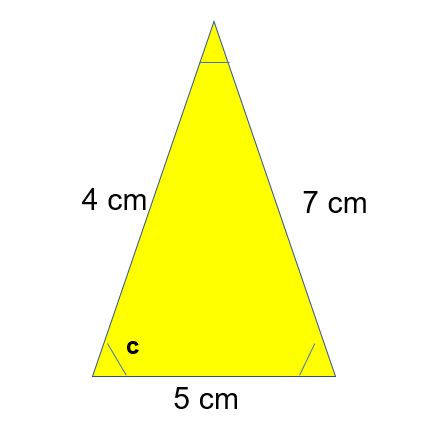
Work out the angle of c:

Once again, take care with your substitution! Cos c = Cos a in the formula!

Finding the area using trigonomic ratios

We can also use trigonometric ratios to find the area of triangles!

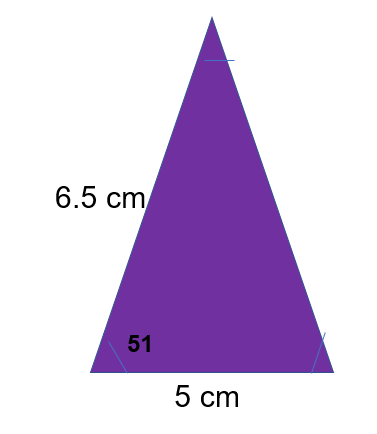
Area of a triangle = 1/2 ABsin(c)

Remember this is you ever need to work out the area of a triangle but don’t have the height or base!

Area of a triangle = 1/2 ABsinc

When substituting in your values remember the little c is the angle that you’ve been given.

Area of a triangle= 1/2 (6.5)(5)sin(51) = 12.63 cm²