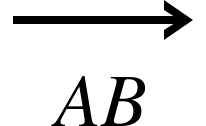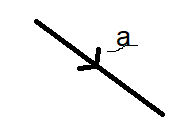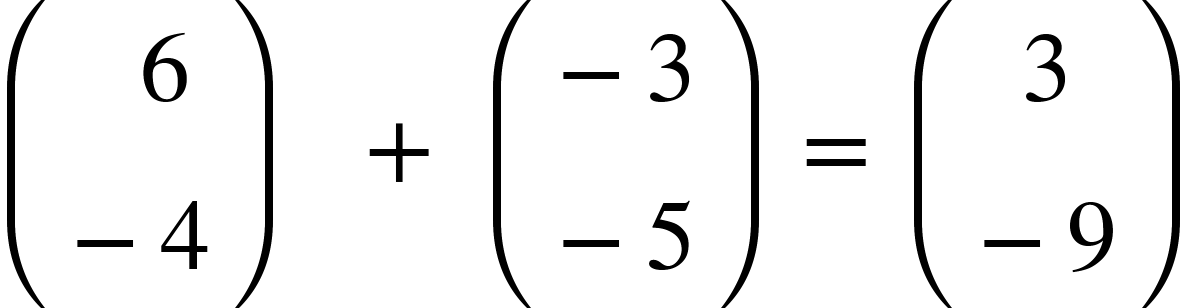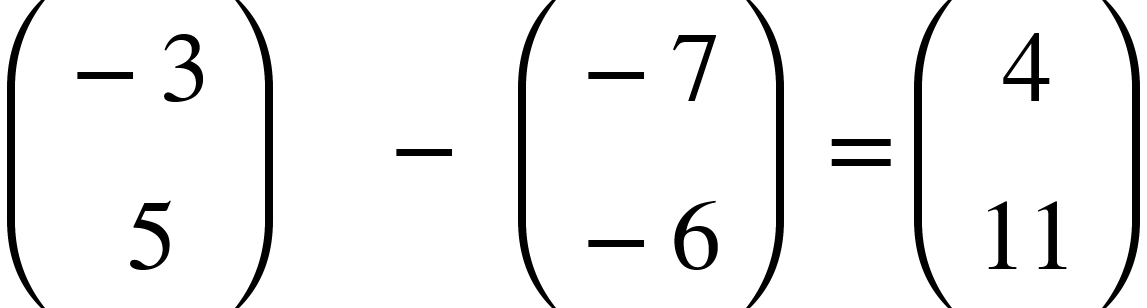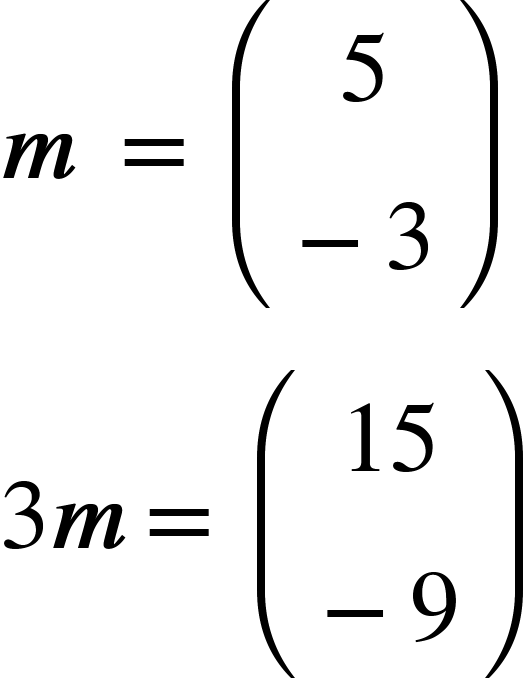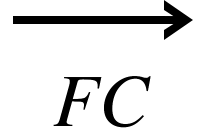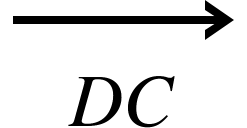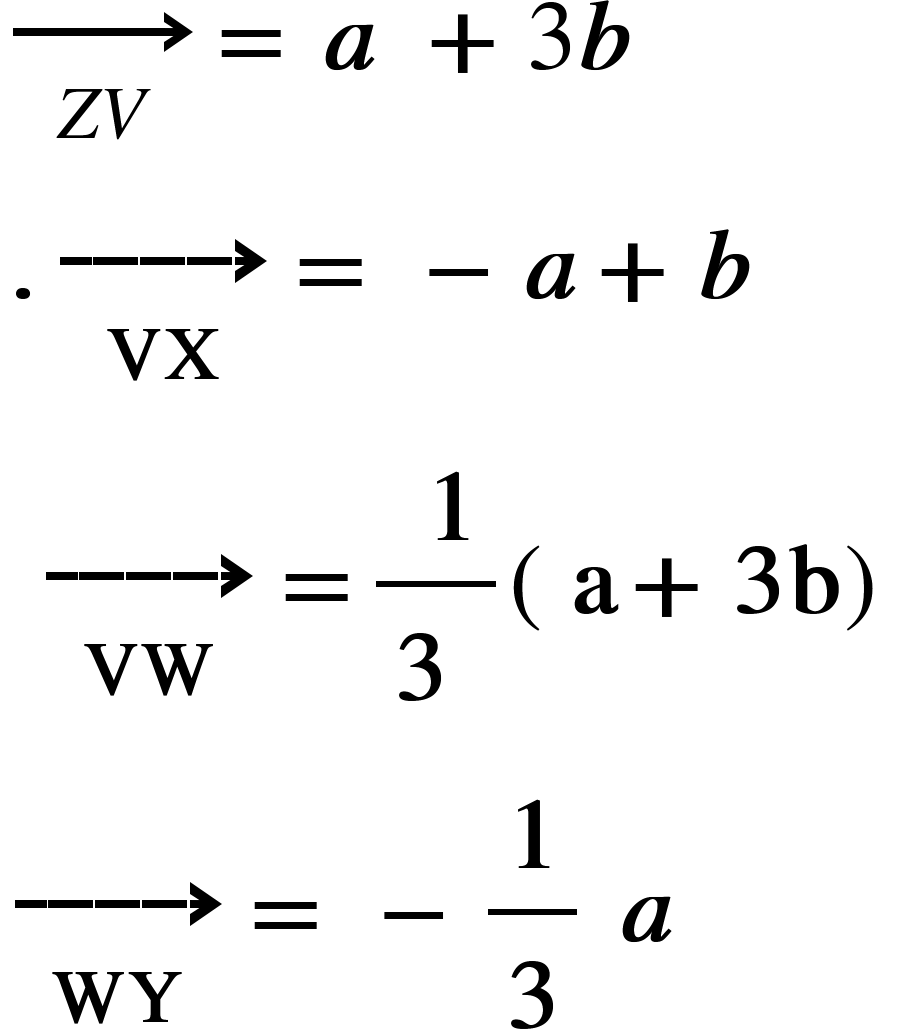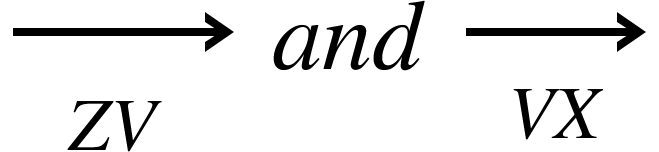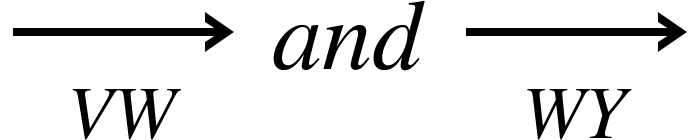Vectors

Describing translations using vectors

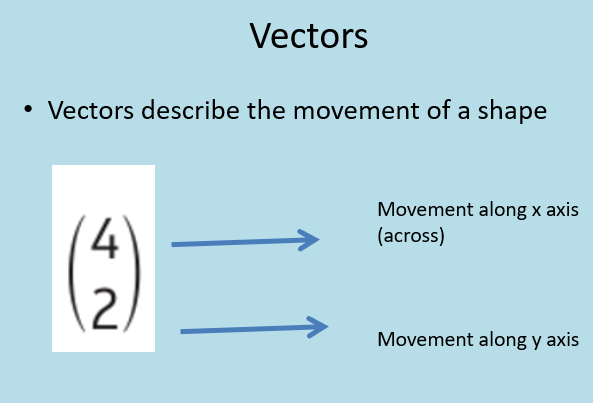
Vectors are used to describe movement. We often use them to describe the movement of shapes on or off of graphs.

We also write vectors like this

which refers to vector AB, this can be a line or two points, point A and point B,. It can also be referred to as a or as below:

Adding Vectors

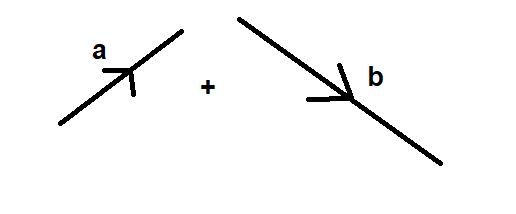
When it comes to adding and subtracting vectors its quite simple, add the x values and add the y values together.

Eg. Adding:

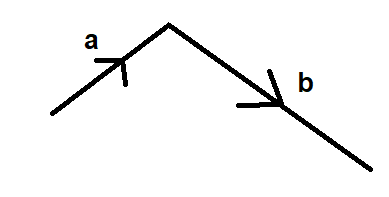
When vectors are added together the arrows follow the same direction eg.

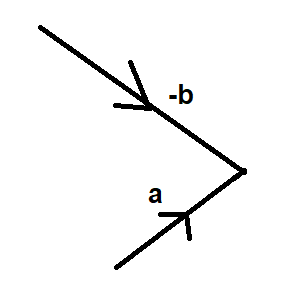
Subtracting Vectors

Eg. Subtracting:

a-b =

Multiplying by a scalar

Vectors have a direction and a magnitude. So for example the vector3a is three times as large asa.

To multiply by a scalar, simply multiply the column vector by the scale factor, or multiply the length by the scalar.

For example:

Diagramatic Vectors

Often, we have vectors put together to describe a shape or a diagram.

For example:

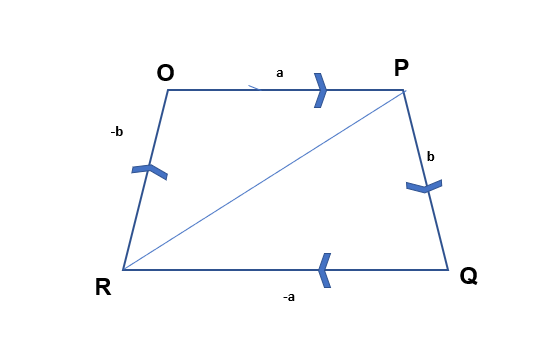
In this diagram we can describe the different lengths in terms of their vectors.

Eg. OP=a PQ=b QR=-a RO=-b and RP =-b + a

You may often need to find vectors that describe how to get from one point of the diagram to the other.

For example:

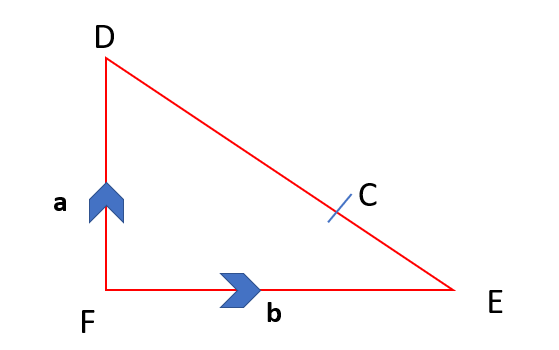
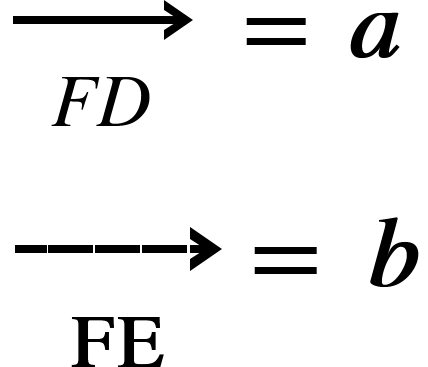
Given that:

And point C is on the line DE such that EC: DC is in the ratio 1:3 find an expression for the line the vector

.

Firstly we need to think about the line DE and how we can express that as a vector.

DE =b-a

Now we need to think about the ratio. We know that the line DE is split in the ratio of 1:3. Thereforeb-a = the whole. When we have a ratio we need to split a whole into equal parts, in this case 1 part to 3 parts.

Therefore

EC: DC

1/4 (b-a) : 3/4 (b-a)

Now we can work out the whole vector

To go from F to D =a

Then we will need to add the vector

which we know is 3/4 (b-a)

a + 3/4 (b-a) =

a + 3/4 b- 3/4 a = 1/4 a +1/4 b

Vectors for proofs

Often you will be required to prove a vector can be written in a certain way or that one vector relates to another in a certain way.

Common things that you may need to prove:

1. That two lines are parallel
2. That a point on a line is a midpoint.

For these specific proofs remember

1. When two lines are parallel they have the same gradient. Therefore if two vectors have a different magnitude but the same letter eg. 4v and2v they are parallel.
2. A midpoint is half of a line, so the scalar of the vector should be ½ of the given vector.

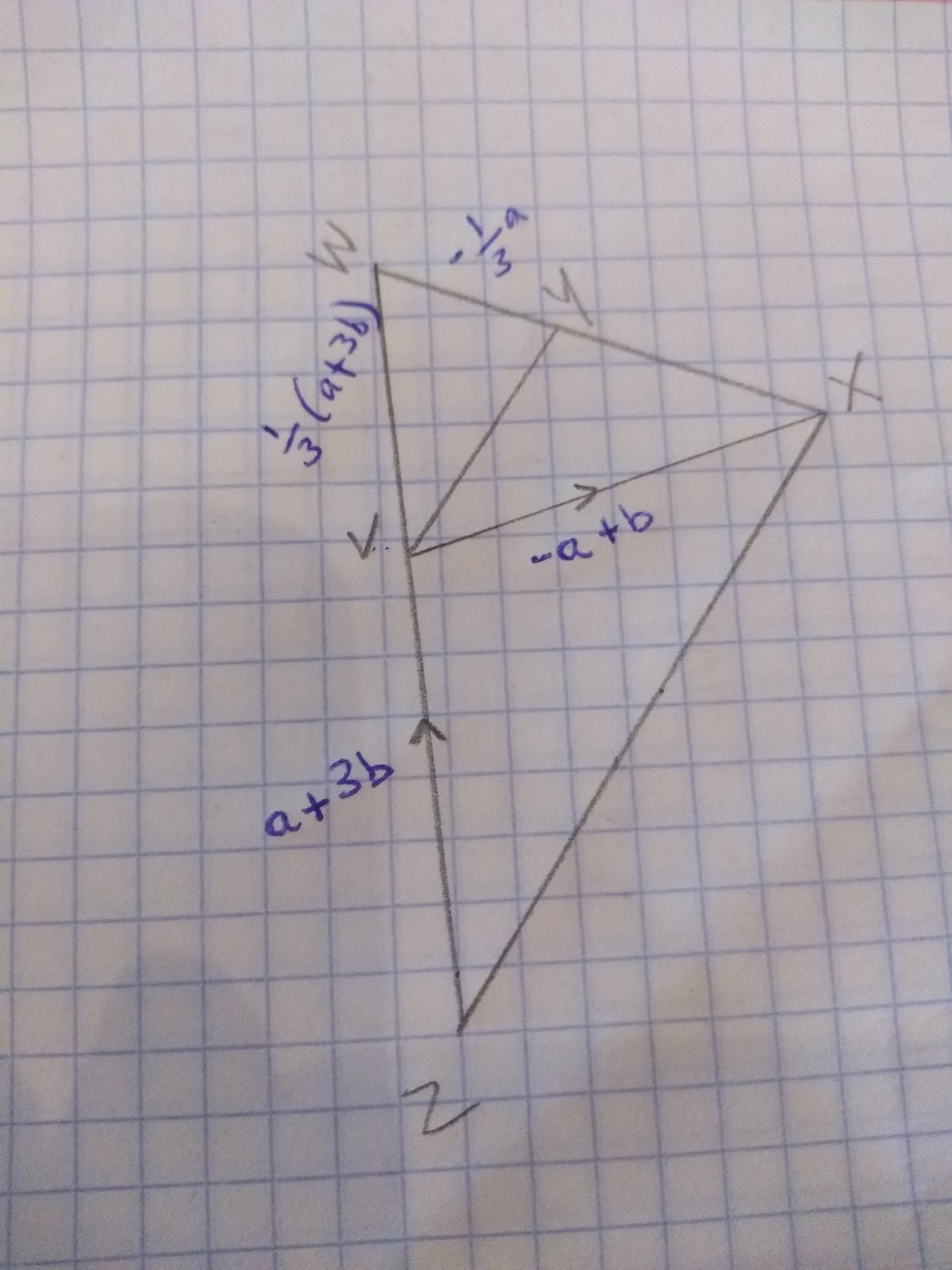
For example to prove that VY is parallel to ZX , given:

Firstly, put all the information you have about the vectors onto the diagram.

To prove that the two lines are parallel we are going to need to find the vectors for both lines.

So, let’s start with the line ZX

We can get from Z to X by adding the vectors

= a + 3b + -a+b

= 4b

Now we just need to work out the vector for the line VY

Which we can get to by adding the vectors

= 1/3(a+3b) + -1/3 a

= 1/3 a +b - 1/3 a

= b

Therefore because b is a factor of 4b the lines must be parallel!