Comparing Measures

Comparing lengths, areas and volumes

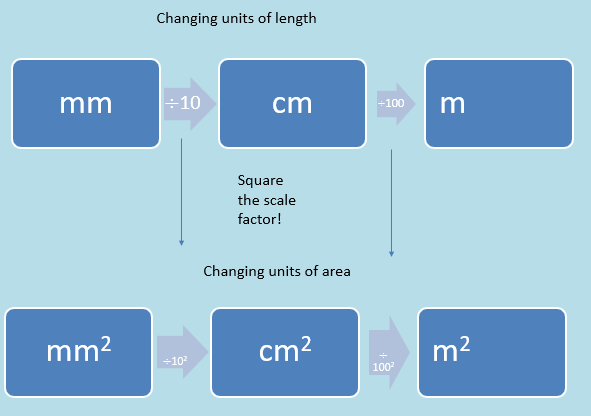
When we want to compare and convert between different lengths we can use the acronym:

1. __K__ing__H__enry__D__ied__U__nusually__Dr__inking__C__hocolate__M__ilk

And this helps us remember how many multiples of 10 we need to increase or decrease to go between different metric units. This is covered in more detail in Comparing Measures.

Area

When we look at area we need to square the scale factor that we use to move between each unit.

Let’s have a look why:

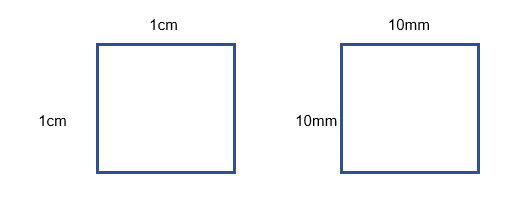
                     Area= 1 cm2                                             Area= 100mm2

Here we have the same square, with the lengths given in cm and the other in mm.

From___ Changing Between Standard Units___ for lengths to go from mm to cm you divide by 10.

However if we look at the units of the area we see that we need to divide by 100 to go from mm² to cm²

Therefore when we convert between areas we square the amount that we multiplied the units when we change the length

This is exactly the same when we go from a larger unit to a smaller unit.

For example to go from 2 m² to cm² we would multiply by 1002.

Volume

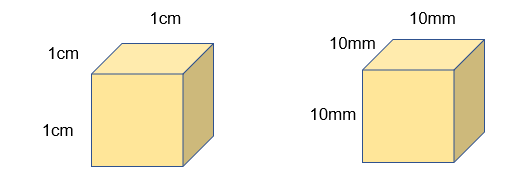
When it comes to volume, we cube the scale factor. For example:

These cubes are the exact same size and have the exact same volume. This shows 1 cm³ = 1000 mm3

Therefore to go from length units to volume units you cube the scale factor!

Example:

What is the volume in ?cm³ of a cuboid that has a volume of 25m³

When we go from m to cm we multiply by 100 therefore we will have to multiply by 1002 .

So: 25 x 1002 = 250,000 cm³

Similarity

When shapes are similar they have the same angles and their lengths are in proportion.

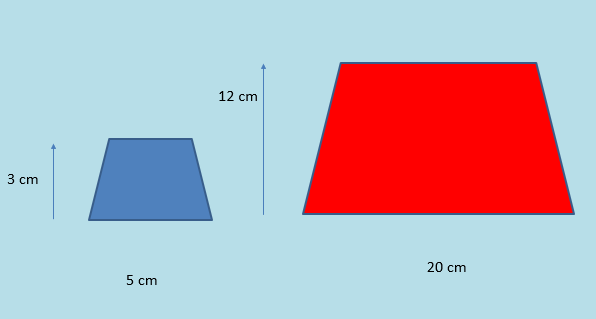
For example these to shapes are similar:

Their angles are the same.

Their lengths are in proportion to each other.

To go from one similar shape to another we multiply by a scale factor.

If a scale factor is less than 1 the shape will get smaller, if it is more than one it will get larger.

Scale Factors

Scale factors tell us how similar shapes relate to each other.

For example:

To go from the blue shape to the red shape you need to enlarge the blue shape by a scale factor of 4.

This means we need to multiply each length by 4.

To go from the red shape to the blue shape we would need to multiply by a scale factor of ¼ .

In this exam you will need to be able to:

1. Identify different scale factors from a given length
2. Identify different scale factors from a given area
3. Identify different scale factors from a given volume
4. Draw or sketch shapes to show how they have changed given a scale factor.

Length

To identify the scale factor between two shapes given their length remember that they are in proportion. You can use this to find the scale factor.

1. To go from a large shape to a small shape: Small/Large
2. To go from a small shape to a large shape: Large/small

This will be your scale factor. Eg.

To go from the blue shape to the red shape:

20/5 = 4 and 12/3 = 4

The scale factor is 4, the lengths will increase.

To go from the red shape to the blue shape:

5/20 = ¼ and 3/12 = ¼

The scale factor is ¼, the lengths will decrease.

Scale factors of areas

When we want to work out the scale factors of areas, we will need to square the scale factor.

For example:

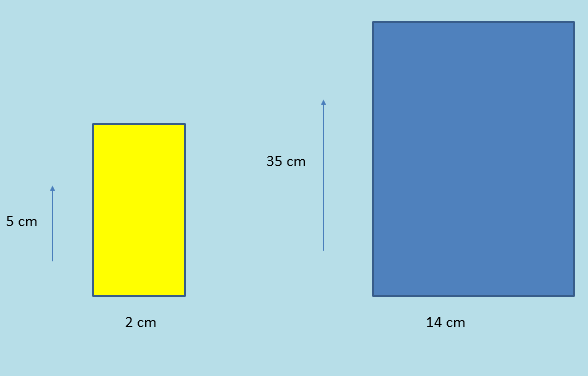
In these two shapes we can see that the linear scale factor to go from the yellow shape to the blue shape is 7.

As 2 x 7 = 14

How do their areas relate?

10 cm² to 490 cm²

This is the same as multiplying by the square of the scale factor

10 x 72 = 490

Volume

When it comes to working out volume, we need to cube the scale factor between the two shapes.

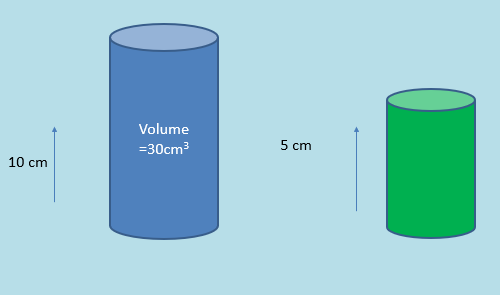
So how to work out the volume using scale factors of lengths?

Step 1: Work out the linear scale factor between the two shapes

In this case 10 to 5 means the scale factor of blue to green will be ½

Step 2: Cube the scale factor and multiply the volume

(½)³ x 30 = 3.75 cm³

A shape has a volume of 45.3m3 how many cm3 is this?

Your answer should include: 45300000 / 45300000cm3

To go from shape A to shape B there is a scale factor of 1.5. The volume of shape B is 200m3. What is the volume of shape A? Give your answer to 3 decimal places.

Your answer should include: 59.259m3 / 59.259m^3 / 59.259