Volume

Volume of cuboids

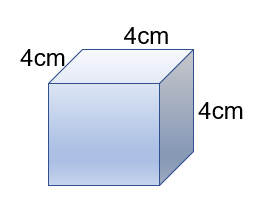
To find the volume of a cube find the length of one side and multiply it by itself 3 times. Eg.:

The volume of this prism is 4cm x 4cm x 4cm = 64 cm³

Volume of prisms

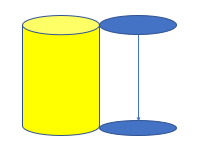
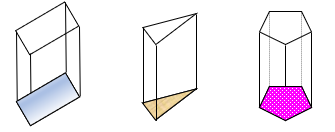
A prism is a 3D shape that’s cross section is the same throughout. Eg:

The circle is the cross section of a cylinder.

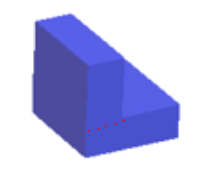
The ‘L’ shape is the cross section of this prism.

In the triangular prism the cross-section is a triangle.

In the pentagonal prism the pentagon is the cross-section.

Therefore to find the volume of a prism:

1. Step 1: Find the area of the cross-section
2. Step 2: Multiply it by the length

Eg. The area of the triangle = 20 cm²

The length is 7 cm

Therefore the volume of the prism = 20cm² x 7cm =140cm³

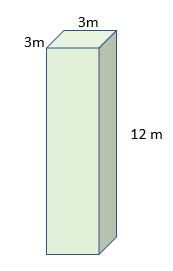
Eg. The cross-section is a square.

The area of the square = 3m x 3m =9m²

The length =12m

Therefore the volume = 3m x 3m x 12m = 108 m³

Remember you may also be asked these questions backwards:

Eg. The volume of this prism is 50m3 and the area of the cross section is 50 cm what is the length?

Remember: 1 m = 100 cm

Volume of a prism = Area of cross-section x length

50m³ = 0.5m x length = 100m

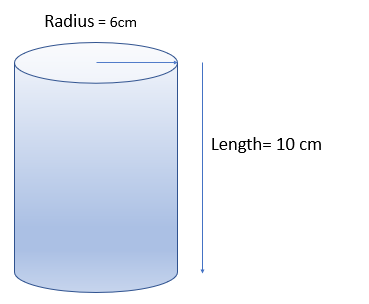
Volume of cylinders

To work out the volume of a cylinder, simply work out the area of the cross-section, in this case the circle and multiply it by the length.

Eg. Area of the circle =π x radius x radius = 36π

Volume = 36π x 10 = 360π or 1,130.97 cm³

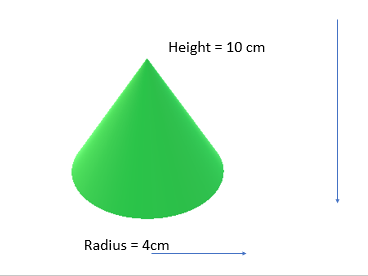
Volume of cones

To find the volume of a cone use the formula:

For example this cone’s volume = π x 4 x 4 x 10/3 = 167.55 cm^3

Volume of spheres

The formula required to work out the volume of a sphere is:

Volume of the sphere =4/3 x π x 8^3 = 2144.66 cm^3

Volume of compound shapes

In order to work out the volume of compound shapes you need to break down a 3D object into different shapes.

For example if you have an L shaped prism such, you would need to split the cross-section into two rectangles, work out their area and then multiply by the length.

The red dotted line is where you could break up your shape.

You may also come across compound shapes that are combinations of spherical shapes, so be prepared to rearrange your formula, half, quarter or divided it by whatever is appropriate.

For example, you might be asked to find the volume of a shape like this:

The radius of the sphere is 10 cm and the height of the cone is 15 cm.

To find the volume of this shape we can divide it into a cone and a semi-sphere.

Therefore, volume of cone:

= π x 102 x 15/3

= π x 100 x 5

= 500π

Half the volume of the sphere =(4/3 x π x 103)/2

= 4000/3 π / 2

= 2000/3 π

Now just to add the two answers together:

2000/3 π + 500 π = 3664.19 cm³